Geekly Articles each Day

補間：PHPとGDを使用してスムーズなグラフィックを描画します

プログラマーの一般的なタスクは、グラフを描くことです。 入力はポイントの配列（x i ; y i ）です。 原則として、グラフの特定のポイントでいくつかの値のみを知っています。 曲線の連続グラフを作成するには、 補間または近似に頼らなければなりません。



補間-与えられた点を通る曲線の構築。
近似は、元の曲線の近似ですが、必ずしも特定の点を通過するわけではありません。

このトピックでは、Lagrange多項式、Cスプライン、Akimaスプライン、およびベジェ曲線の近似を使用して補間するPHPのライブラリを紹介します。 さらに、セグメントのレンダリングをスムージング（アンチエイリアス）で実装します。

補間法と近似法について簡単に検討します。


区分的線形補間


最初に頭に浮かぶのは、ポイントとセグメントを接続することです。



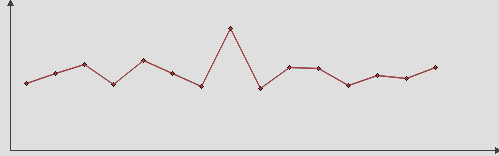
速度の最適なソリューションですが、結果のスケジュールが壊れています-これは必要なものではありません。

ラグランジュ補間多項式


n + 1ポイントの次数nの多項式。 その式は非常に簡単です。



実装は簡単ですが、2つの重大な欠点があります。
1）かなりの量の計算が必要
2）指定されたポイント（ノード）間で予期しない動作をする



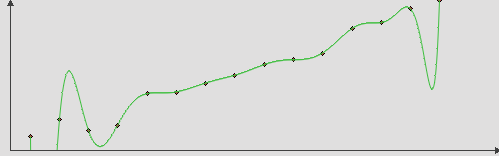
3次スプライン（c-スプライン）


3次スプラインには、前の方法の欠点がありません。 ノード間の各間隔に対して、最大3の次数の多項式が指定されますが、関数の1次および2次導関数は連続でなければなりません。 一方では、これは計算を簡素化し、他方では、曲率の突然のジャンプを回避します。



Wikipediaから取得したC＃コードから3次スプラインの実装を移植しました。

スプラインアキムス


3次スプラインには欠点があります。隣接点から遠く離れた点の近くでは、このようなスプラインは予期しない「外れ値」を引き起こす可能性があります。 この問題は、アキムヒロシによって提案されたスプラインを使用して解決できます。 注意-Akimaスプラインはより安定しています：



David Freyの debian asplineプログラムCコードからAkimaスプラインの実装を移植しました。

ベジェ曲線近似


場合によっては、与えられた点を通る曲線を描くのではなく、それらを参照点として使用すると便利です。 これにはベジェ曲線法が役立ちます（C＃からTolg Birdalの例を移植しました）。 曲線は最初と最後の点を通過します



性能試験


Xeon 5560 2.8GHzサーバーでレンダリングせずに500x500サイズのグラフで実行され、実験数=1000。平均実行時間、s：
ポイント数：51550
ラグランジュ多項式1.7895.66420.446
3次スプライン0.1530.2300.313
スプラインアキムス0.0170.0240.049
ベジェ曲線0.2440.2760.304

以下の表から次の結論を引き出すことができます。
1）ラグランジュ多項式の計算時間は、ポイント数の増加とともに急速に増加します。
2）Akimaスプラインは3次よりも速く動作します。
3）ベジェ曲線の作成は、スプラインよりも遅くなります。

メソッド選択


最初に考えてください：ポイント間に曲線を描く必要さえありますか？ ポイントが少ない場合、テーブルを使用する方が良いでしょうか？ グループ化範囲の統計（たとえば、長期データでの月の平均気温）を扱う場合は、ヒストグラムを使用することをお勧めします。

既知の点を通る曲線を描く必要がある場合は、Akimaスプラインの使用をお勧めします。 ポイント自体が大きな役割を果たさない場合は、ベジェ曲線のグラフを近似します。

アンチエイリアス


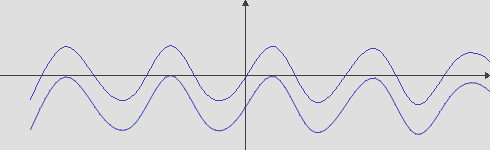
gdライブラリで曲線を作成するには、セグメントを作成します。 これを行うには、曲線を特定のステップ（少なくとも1ピクセル）のセクションに分割し、セクションの開始と終了の間に、関数imagelineでセグメントを描画します。 ただし、PHPのこのセグメントは、アンチエイリアスなしでレンダリングされます。 画面の平滑化を使用してセグメントを描画するアルゴリズムは、Wuアルゴリズムに役立ちます。 Wuアルゴリズムは、±45°の角度でのみセグメントを描画できるため、他の場合は「回転」する必要があります。 この図は、アンチエイリアスなしの関数sin（x）のグラフを示し、アンチエイリアスなしの関数は下にありません。



図書館


各補間法/近似法について、LagrangePolynomial、CubicSpline、AkimaSpline、BezierCurveという個別のクラスを作成しました。 各クラスには3つのパブリックメソッドがあります。
setCoords（＆座標、ステップ、[x_min、[x_max]]）-曲線構築の初期座標とパラメーターを設定し、エラーの場合はfalseを返します
process（）-曲線を構築するための座標の配列を返します
getError（）-エラーメッセージを返します
座標は配列配列として転送されます（x1 => y1、x2 => y2 ... xn => yn）

プロットするために、補助クラスPlotが実装されています。 その機能は非常に控えめです（たとえば、スケーリングはありません-グラフは1対1でプロットされます）。その代わりに、別のクラスまたはネイティブPHP関数を使用できます。 方法
コンストラクターは座標の配列を受け取ります。
drawLine（image、color、[x0、[y0]]）-破線を描画します。画像はリソース識別子です。色はimagecolorallocateに設定する必要があります。x0およびy0は原点オフセットです（デフォルトでは、画像の左下隅にあります）
drawAALine（image、color、[x0、[y0]]）-アンチエイリアスセグメントで破線を描画します。パラメーターはdrawLineに似ています
drawDots（image、color、[x0、[y0、[size]]]）-セグメントを接続せずにポイントを描画します。パラメーターはdrawLineに似ています。サイズはポイントの直径です
drawAxis（image、color、[x0、[y0、[1sq]]]）-軸を描画します。パラメータはdrawLineに似ています。1sq= true（デフォルト）の場合、軸は最初の象限にのみ描画されます-正の方向

例（関数sin（x））：
<？php
//便宜上、事前にサイズを設定します
define （ 'GRAPH_WIDTH' 、 490 ） ;
define （ 'GRAPH_HEIGHT' 、 150 ） ;

//汎用抽象クラスSmoothCurve
include_once （ 'SmoothCurve.class.php' ） ;

// 3次スプラインクラス
include_once （ 'CubicSpline.class.php' ） ;

//使用することもできます
// include_once（ 'AkimaSpline.class.php'）;
// include_once（ 'BezierCurve.class.php'）;

//チャート作成のヘルパークラス
//代わりに、独自のまたはネイティブのPHP関数を使用できます
include_once （ 'Plot.class.php' ） ;

//配列の座標を設定します（x1 => y1、x2 => y2 ... xn => yn）
$ testCoords [ -215 ] = -24.2705098312 ;
$ testCoords [ -180 ] = 28.5316954889 ;
$ testCoords [ -145 ] = -9.27050983125 ;
$ testCoords [ -110 ] = -17.6335575688 ;
$ testCoords [ -75 ] = 30 ;
$ testCoords [ -40 ] = -17.6335575688 ;
$ testCoords [ -5 ] = -9.27050983125 ;
$ testCoords [ 30 ] = 28.5316954889 ;
$ testCoords [ 65 ] = -24.2705098312 ;
$ testCoords [ 100 ] = 0 ;
$ testCoords [ 135 ] = 24.2705098312 ;
$ testCoords [ 170 ] = -28.5316954889 ;
$ testCoords [ 205 ] = 9.27050983125 ;
$ testCoords [ 240 ] = 17.6335575688 ;
$ testCoords [ 275 ] = -30 ;

//トゥルーカラーイメージを作成します（アンチエイリアス用）
$ im = imagecreatetruecolor （ GRAPH_WIDTH 、 GRAPH_HEIGHT ） ;

//色を設定します
$ bgColor = imagecolorallocate （ $ im 、 224、223、223 ） ;
$ textColor = imagecolorallocate （ $ im 、 0、0、0 ） ;
$ axisColor = imagecolorallocate （ $ im 、 64、64、64 ） ;
$ dotColor = imagecolorallocate （ $ im 、 192、64、64 ） ;
$ graphColor = imagecolorallocate （ $ im 、 64、64、192 ） ;

//バックグラウンド
imagefill （ $ im 、 0、0 、 $ bgColor ） ;

//チャートオブジェクトを作成します
$ testGraph = new Plot （ $ testCoords ） ;
//オプション：既知の点を描画します
// GRAPH_WIDTH / 2とGRAPH_HEIGHT / 2を渡すと、画像の中心に原点が移動します
$ testGraph- > drawDots （ $ im 、 $ dotColor 、 GRAPH_WIDTH / 2 、 GRAPH_HEIGHT / 2、5 ） ;

//スプラインオブジェクトを作成します
$ curve = new CubicSpline （ ） ;
//座標を渡し、レンダリングステップ= 5
$カーブ -> setCoords （ $ testCoords 、 5 ） ;
if （ ！ $ curve- > getError （ ） ）
{
//曲線の座標の計算
$ curveCoords = $ curve- > process （ ） ;
if （ $ r ）
{
//別のチャートオブジェクト
$ curveGraph = new Plot （ $ curveCoords ） ;
//曲線を描く
$ curveGraph- > drawLine （ $ im 、 $ graphColor 、 GRAPH_WIDTH / 2 、 GRAPH_HEIGHT / 2 ） ;
}
}

//ユーザーに与える
header （ "Content-type：image / png" ） ;
imagepng （ $ im ） ;
imagedestroy （ $ im ） ;
？>


ライブラリとデモ版をダウンロード

藤堂




文学


E.P. クズミン、D.V。 コンピュータグラフィックスのIvanovアルゴリズムの基礎（講義番号4）
スプライン補間
Akimsによるオリジナル記事
キュービックとスプライン秋間の比較
ベジエ曲線をシンプルに

ウィキペディア：
ラグランジュ多項式 。
3次スプライン
ベジェ曲線

Source: https://habr.com/ru/post/J130873/

More articles:


All Articles