科学ニュース：マトリックスサイズ
今乗算する方法を知っています
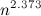
。 言い換えれば、それは証明されています
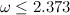
どこで
-
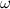
行列乗算の指数 。 最近、
Virginia Vasilevska-Williamsがこれを証明し、それにより推定を改善しました
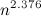
1987年にコッパースミスアンドグレープによって取得されました。 このアルゴリズムの重要性についてはかなり書きます。 さらに学ぶことに興味がある人は、
スコット・アーロンソン 、
リチャード・リプトン 、
ビル・ガザルシュの投稿を読んで
ください 。
そのため、アルゴリズムの実行時間の多くの理論上の上限は、行列乗算指数を使用します。 特に、多くのグラフアルゴリズムはこの考えを活用しています。Aがグラフ隣接行列の場合、
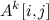
-頂点iとjの間の長さkのパスの数（必ずしも単純ではありません！）。 このシンプルなアイデアは時間を許します
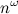
グラフに三角形があるかどうかを確認します（3クリック）：隣接行列を立方体に構成する必要があり（このためには2つの行列乗算が必要です）、対角線を見てください。 ここでは、高度な行列乗算アルゴリズムが漸近的に単純なキュービックアルゴリズムよりも優れているため、理論上の推定値について説明していることに注意してください。
さらにいくつかの例：
- 頂点のすべてのペア間の距離（すべてのペアの最短パス）。
重み付けされていないグラフの頂点のすべてのペア間の最短パスは、時間内に見つけることができます 
。 これを行うには、隣接行列をn乗し（したがって、o（1）が累乗します）、同時に最短経路を計算します。 詳細、および他の多くの同様のエレガントなアルゴリズムを見つけることができます
Uri Zwickによる素晴らしいプレゼンテーション。 - 最大2実行可能性の問題（MAX-2-SAT）。
完全な検索よりも高速に動作するこのタスクの唯一の既知のアルゴリズム（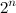 
）、これも行列乗算に基づいています。 彼の作業時間は等しい 
そして、指数メモリを使用します。 一言で言えば、アイデアはこれです：入力式を使用して、巨大なグラフを構築します（上に 
頂点）と高速行列乗算を使用して、三角形が含まれているかどうかを確認します。 彼が夫バージニア州のライアン・ウィリアムズを発明したことは注目に値します。 - ハミルトニアンウェイ（ハミルトニアンサイクル）。
マトリックスを乗算できる量がそれほど重要ではないという面白い例がまだありますが、それでもなおです。 時間内にハミルトニアン経路を見つけるためのアルゴリズム 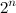多項式メモリ（この問題の有名なHeld-Karpアルゴリズムは動的計画法に基づいており、指数メモリが必要です）：上記のトリックを使用して、グラフ頂点のすべてのサブセットで長さn-1のパスの数を計算します。 この後、包含/除外式を使用すると、見つかった数を合計できるため、長さn-1の単純なパスの数だけが残ります（これがハミルトニアンパスです）。