こんにちは、Habrosociety!
habrには、セグメントツリー、duchaなど、多くの興味深いデータ構造の説明があります。 複雑なデータ構造に興味があるなら、catへようこそ!
私の記事シリーズでは、さまざまなタイプのヒープと、それらを実行する方法について説明します。
1)
二項パイル2)
左ヒープ3)
フィボナッチ束4)
これらのデータ構造を実践する問題文:オブジェクトの多くが(タスクによって異なる)格納されるデータ構造を構築するために、各オブジェクトにはキーフィールドがあり、それによって最小要素をすばやく見つけることができます。 この構造では、次の操作が可能です。
Make新しい空のヒープを作成し、
Insert -ヒープに新しい要素を挿入し、
Minimum -最小キー、
ExtractMin最小抽出、
Merge -2つのヒープを
Mergeし、
Decrease -キー削減、
Delete -オブジェクトを削除します。
多くは、配列:)やバイナリヒープなど、この構造を実装する最も簡単な方法に精通しています。 それらの単純さと一般的な知識のために、私はそれらについて詳しく説明しません。
ご存知のように、
バイナリヒープの場合 、上記の操作の漸近的な動作は次のとおりです。
Make -O(1)
Merge -O(N)
Insert -O(ログN)-Nはヒープ内の要素の数です。
Minimum -O(1)
ExtractMin -O(ログN)
Decrease -O(ログN)
Delete -O(ログN)
バイナリヒープのアルゴリズムについては説明しません。Habréを含め、至る所で繰り返し説明されているからです。 バイナリヒープに慣れていない人のために、読み続ける前にバイナリヒープに慣れることをお勧めします。
次に、
二項ヒープと呼ばれるより興味深いデータ構造を考え
ます 。
二項パイル二項パイルは、いくつかの制限がある
二項ツリーのセットです。 少し後で紹介します。
二項ツリーは、再帰的に定義されるツリーです。
B
iはB
i-1であり、ツリーB
i-1は根の左息子になりました。
B
0はトップです。
B
0 、B
2 、B
3の例 :
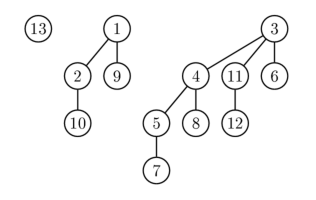
二項ツリー(B
k )には、多くの興味深い
特性があり
ます 。
T.1。 2
kピーク
T.2。 木の高さk
T.3。 深さiのC
i k頂点(これが二項と呼ばれる理由です:C
i kは二項係数です)。
T.4。 ルートの子は、B、B
k-2 、...、B
0-の順です。
T.5。 二項ツリーOの最大頂点の高さ(log N)
特性は帰納法によって
証明されます。 木をよりよく理解するために、読者自身に証明を行うように勧めます。
それで、
二項ヒープに戻り
ましょう 。
二項パイルは二項ツリーのセットであり、次の制限があります。
1)各二項ツリーでは、ヒーププロパティが保持されます。
2)同じサイズの2つのツリーがない
3)ツリーはサイズ順に並べられます。
二項ヒープがプログラムにどのように保存されるかについて話しましょう。 「左の息子-右の兄弟」メソッドを使用します。 ルートリスト(
root_list 、その長さは
root_list.length )を保存します。このリストには、二項式ツリーのルートが、高さの順に並んでいます。 各頂点には次のフィールドがあります。
data一番上に保存されるデータ(これにより最小値が見つかります)
right -右兄弟
child -左の息子
degree-頂点の次数(明らかに、二項ヒープ内のツリーはこのフィールドによって順序付けられます)
すぐに気づく:プロパティ H.1:
root_list.length = O(log N)の長さ。Nはヒープ内の要素の数です。
証明のために、T.1のために、数値のバイナリ表記でツリーB
kが存在することに注意するだけで十分です。
二項ヒープで実行できる操作の説明に移りましょう。
作るタスク :空のヒープを作成します。
アルゴリズム :空の
root_list作成します。
難易度 :明らかに、実行時間はO(1)です。
マージタスク :2つのヒープを1に結合します。
アルゴリズム :最初に、ヒープルートリストを1つのルートリストに結合し、次数の順序を維持します。 このアルゴリズムは、mergeSortで2つの配列をマージすることに似ています。
リストの先頭へのポインターで保存し、結果のリストに最小リストを書き込みます。書き留めたリストは次のリストに移動します。 次に、受信した新しいルートリストの最初から最後まで移動し、同じサイズのツリーを1にマージします。
1)同じサイズの2つのツリーのみ。 次にそれらを結合します。
2)同じサイズの3本の木。 最後の2つを組み合わせます。
2つのツリーを結合するときは、一方のキーの方が小さいキーを見て、もう一方のツリーをこのツリーのルートの左息子にするだけで済みます。
2つのヒープを結合した後に何が起こるかの例:
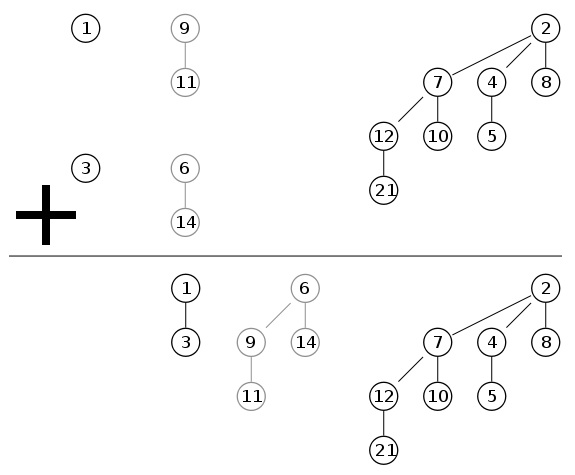 難しさ
難しさ :
root_list1.length時間O(
root_list1.length )+ O(
root_list2.length )=(プロパティH.1による)= O(log N)。
1つのパス(O(log N))で、結合二項ツリーを取得します。 総複雑度はO(log N)であることがわかります。
挿入タスク :ヒープに新しいアイテムを挿入します。
アルゴリズム :1つの要素の束を作成し、その束と組み合わせます。
難易度 :O(1)+ O(log(N))= O(log(N))
最低タスク :ヒープ上の最小値を見つけます。
アルゴリズム :明らかに、最小値はルートリストにあります。つまり、それを見つけるにはルートリストを調べる必要があります。
難易度 :O(
root_list.length )= O(ログ(N))。
エキスミンタスク :最小要素を削除します。
アルゴリズム :
Minimumを使用して検索します。 ルートリストから削除します。 彼の子のインバーテッドリストから、新しいヒープ(H
1 )のroot_listを作成し、元のヒープをH
1と結合します。
難易度 :最小値を抽出する各操作はO(log N)で機能するため、O(log N)+ O(log N)+ O(log N)= O(log N)
減らすタスク :この頂点のデータ値を減らします。
アルゴリズム :上部の値を減らします。 次に、ヒーププロパティがピークとその先祖に対して違反される可能性があります。その後、それらの場所を変更します。 ピークがその場所に「現れる」まで、このプロセスを続けます。 このアルゴリズムは、バイナリヒープのアルゴリズムと同じように機能します。
難易度 :最悪の場合、頂点はルートにポップアップします。つまり、O(log N)アクションを実行します(各ステップの頂点は1レベル高くなり、二項ツリーの高さはT.5 O(log N)です)
削除するタスク :任意の要素を削除します。
アルゴリズム :最初に、減少を使用して、頂点の値を可能な限り最小にします。 そして、ヒープの最小値(
ExtractMin )を削除します。
難易度 :O(log N)+ O(log N)= O(log N)
おわりに二項ヒープのデータ構造を調べ、その漸近的な動作を証明しました。
次の記事では、二項ヒープに基づいて、やや複雑なデータ構造、つまりフィボナッチヒープを構築します。
rain.ifmo.ru/cat/view.php/vis/heaps/binomial-2001で二項ヒープを
いじることができます
。T.Kormenの「アルゴリズム:構築と分析」で詳細を読むことができます。
ご清聴ありがとうございました。またお会いしましょう!