Geekly Articles each Day

ファジー推論ルールを使用した選択肢の多基準選択。 Java実装。 パート3/3：例

前のパーツ：
  1. ファジー推論ルールを使用した選択肢の多基準選択。 パート1/3：理論
  2. ファジー推論ルールを使用した選択肢の多基準選択。 Java実装。 パート2/3：基本的なアルゴリズム


書籍の例は次のとおりです。Borisov、Krumberg、Fedorov-「ファジィモデルに基づく意思決定。 使用例」、1990年。 94-102

状態。 研究所のリーダーシップは、教員の空席を埋める候補者を検討しています。 タスクは、上記の方法を使用して、それらのベストを特定することです。 教員のメンバー間の議論により、次の結果が得られました。
d1：「候補者が経験豊富な研究者であり、ある程度の実務経験と技術分野の指導経験がある場合、候補者は満足です（要件を満たしている）。

d2：「上記の要件に加えて、彼が情報システムの理論を教えることができれば、彼は満足している以上です」。
d3：「d2に加えて、彼がハイテク製品の顧客を見つける能力を持っているなら、彼は申し分ない」

d4：「情報システムの理論を教える能力を除いて、opがd3で規定されているすべてのものを持っている場合、彼は非常に満足しています」。
d5：「候補者が非常に経験豊富な研究者であり、顧客と優れた教師を見つける能力はあるが、制作経験がない場合でも、彼は満足できるでしょう。」
d6：「彼が研究者の資格を持っていないか、教える能力が証明されていない場合、彼は不十分です。」



6つの情報フラグメントの分析により、意思決定に使用される5つの基準が得られます。
X（1）-研究能力;
X（2）-生産経験
X（3）-技術分野の指導経験
X（4）-情報システムの理論を教えた経験
X（5）-顧客を見つける能力。

U候補の基本セットでこれらの変数を測定します。 6つのフラグメントを見ると、次のようになります。
画像

行A、B、C、D、Eから、入力インターフェイスを実装する入力クラスのmakeSkillメソッドに渡されるマトリックスがコンパイルされます。 その説明を以下に示します（ステートメントの変換を参照）。

ファジー機能

その後、知識の断片は次の形式を取ります。
d（1）：「X = A、B、Cの場合、Y = S」
d（2）：「X = A、およびB、C、およびDの場合、Y = MS」
d（3）：「X = A、B、C、D、Eの場合、Y = P」
d（4）：「X = A、およびB、C、およびEの場合、Y = VS」
d（5）：「Xが非常にAで、B、C、およびEではない場合、Y = S」
d（6）：「X = AでもCでもない場合、Y = US」

上記に従って、実装内の機能の内容：

package Function; import Support.Function; public class mMS extends Function { /*,  */ public mMS(){} public double getY(double x) { return x*Math.sqrt(x); } } 


 package Function; import Support.Function; public class mP extends Function{ /**/ public mP(){} public double getY(double x) { if (x==1) return 1; return 0; } } 

 package Function; import Support.Function; public class mVS extends Function{ /* */ public mVS(){} public double getY(double x) { return x*x; } } 

 package Function; import Support.Function; public class mS extends Function { /**/ public mS(){} public double getY(double x) { return x; } } 

 package Function; import Support.Function; public class mUS extends Function{ /* */ public mUS(){} public double getY(double x) { return 1-x; } }


音声変換

ルールを使用してこれらのステートメントを変換すると、

画像

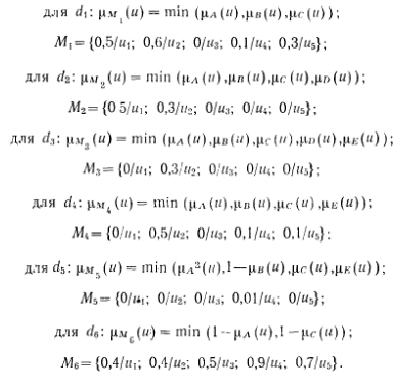
ルールを必要なスキルに関連付ける入力クラスは次のとおりです。

 package FLO_Engine; import Support.Function; import Support.Input; import Support.Rule; import Support.Skill; public class input extends Input{ private Skill A,B,C,D,E,A_M5,B_M5,A_M6,C_M6; public input(){ /*        */ PARAMS_CNT = 5; FUNC_CNT = 6; } public void initFunc(Function[] func){ this.func = func; } private void makeSkill(double[][] arr){ /*     ;       ,   Function        */ rl = new Rule[FUNC_CNT]; A = new Skill(arr[0]); B = new Skill(arr[1]); C = new Skill(arr[2]); D = new Skill(arr[3]); E = new Skill(arr[4]); double[][] u=arr; double[] a_m5 = (double[]) u[0].clone(); for (int i=0;i<u[0].length;i++) a_m5[i]*=a_m5[i]; /* */ A_M5 = new Skill(a_m5); double[] b_m5 = (double[]) u[1].clone(); for (int i=0;i<u[1].length;i++) b_m5[i]= 1 — b_m5[i]; /*   */ B_M5 = new Skill(b_m5); double[] a_m6 = (double[]) u[0].clone(); for (int i=0;i<u[0].length;i++) a_m6[i] = 1 — a_m6[i]; /*   */ A_M6 = new Skill(a_m6); double[] c_m6 = (double[]) u[2].clone(); for (int i=0;i<u[2].length;i++) c_m6[i] = 1 — c_m6[i]; /*   */ C_M6 = new Skill(c_m6); } public Rule[] makeRules(double[][] arr) throws Exception{ makeSkill(arr); rl[0] = new Rule(new Skill[]{A,B,C} ,func[0]); //  d1 rl[1] = new Rule(new Skill[]{A,B,C,D} ,func[1]); //  d2 rl[2] = new Rule(new Skill[]{A,B,C,D,E} ,func[2]); //  d3 rl[3] = new Rule(new Skill[]{A,B,C,E} ,func[3]); //  d4 rl[4] = new Rule(new Skill[]{A_M5,B_M5,C,E} ,func[4]); //  d5 rl[5] = new Rule(new Skill[]{A_M6,C_M6} ,func[5]); //  d6 return rl; } }


このように
d（1）：「X = M（1）の場合、Y = S」
d（2）：「X = M（2）の場合、Y = MS」
d（3）：「X = M（3）の場合、Y = P」
d（4）：「X = M（4）の場合、Y = VS」
d（5）：「X = M（5）の場合、Y = S」
d（6）：「X = M（6）の場合、Y = US」

画像

計算

対応する式を使用して、各ステートメントの行列Dを取得します。
画像
コードの結果：
D [1]：
0.5 0.60 0.70 0.80 0.9 1.0 1.0 1.0 1.0 1.0 1.0 1.0
0.4 0.50 0.60 0.70 0.8 0.9 1.0 1.0 1.0 1.0 1.0 1.0
0.5 0.60 0.70 0.80 0.9 1.0 1.0 1.0 1.0 1.0 1.0 1.0
0.9 1.00 1.00 1.00 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
0.7 0.79 0.89 1.00 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0

画像
D [2]：
0.5 0.53 0.58 0.66 0.75 0.85 0.96 1.0 1.0 1.0 1.0
0.7 0.73 0.78 0.86 0.95 1.00 1.00 1.0 1.0 1.0 1.0
0.5 0.53 0.58 0.66 0.75 0.85 0.96 1.0 1.0 1.0 1.0
0.9 0.93 0.98 1.00 1.00 1.00 1.00 1.0 1.0 1.0 1.0
0.7 0.73 0.78 0.86 0.95 1.00 1.00 1.0 1.0 1.0 1.0
ここでは結果は収束しませんが、MATLABと工学計算機は私の側にあります。 ほとんどの場合、これは著者の誤算です。

画像
D [3]：
0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 1.0
0.7 0.7 0.7 0.7 0.7 0.7 0.7 0.7 0.7 0.7 0.7 0.7 1.0
0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 1.0
0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 1.0 1.0
0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9 1.0 1.0
同じ話、おそらく著者の計算の関数の1つはエラーでした。

画像
D [4]：
0.5 0.51 0.54 0.59 0.66 0.75 0.86 0.99 1.0 1.0 1.0
0.5 0.51 0.54 0.59 0.66 0.75 0.86 0.99 1.0 1.0 1.0
0.5 0.51 0.54 0.59 0.66 0.75 0.86 0.99 1.0 1.0 1.0
0.9 0.91 0.94 0.99 1.00 1.00 1.00 1.00 1.0 1.0 1.0
0.9 0.91 0.94 0.99 1.00 1.00 1.00 1.00 1.0 1.0 1.0

画像
D [5]：
0.50 0.6 0.7 0.8 0.9 1.0 1.0 1.0 1.0 1.0 1.0 1.0
1.00 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
1.00 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
0.99 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
1.00 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0

画像
D [6]：
1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.00 1.00 0.90 0.8
1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.00 1.00 1.00 0.9
1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.00 1.00 1.00 1.0
1.0 1.0 1.0 1.0 1.0 1.0 1.0 0.99 0.89 0.79 0.7
1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.00 1.00 1.00 1.0

一般的な関数解Dは、ファジーセットD（i）の共通部分として見つかります。
画像

D：
0.5 0.50 0.50 0.50 0.50 0.5 0.5 0.5 0.50 0.50 0.8
0.4 0.50 0.54 0.59 0.66 0.7 0.7 0.7 0.70 0.70 0.9
0.5 0.50 0.50 0.50 0.50 0.5 0.5 0.5 0.50 0.50 1.0
0.9 0.90 0.90 0.90 0.90 0.9 0.9 0.9 0.89 0.79 0.7
0.7 0.73 0.78 0.86 0.90 0.9 0.9 0.9 0.90 0.90 1.0

結果の不一致の考えられる理由は上記のとおりです。次に、本との比較を使用して、「より正確」であることが判明した決定の一般的な流れを示します。 式は同じですが、この実装、MATLAB、電卓は私の好意を表しています。 教科書の著者は一桁以上の経験がありますが、計算の方法は不明です-本の唯一のコピーが1990年代の日付であり、同じエラーを除外することはできません。

ポイントスコアの計算

画像

私の結果：
オブジェクト＃1：
E：0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.8
X：0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
推定ポイント：0.6875

画像
オブジェクト＃2：
E：0.4 0.5 0.54 0.59 0.66 0.7 0.7 0.7 0.7 0.7 0.9 0.9
X：0.0 0.1 0.20 0.30 0.40 0.5 0.6 0.7 0.8 0.9 1.0
推定ポイント：0.6561

画像
オブジェクト＃3：
E：0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 1.0
X：0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
ポイント見積もり：0.7500

画像
オブジェクト＃4：
E：0.7 0.79 0.89 0.9 0.9 0.9 0.9 0.9 0.9 0.9 0.9
X：0.0 0.10 0.20 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
ポイント見積もり：0.4833

画像
オブジェクト＃5：
E：0.7 0.73 0.78 0.86 0.9 0.9 0.9 0.9 0.9 0.9 1.0
X：0.0 0.10 0.20 0.30 0.4 0.5 0.6 0.7 0.8 0.9 1.0
ポイント見積もり：0.5757308868523388

画像

明らかに、3番目の選択肢が最適です（スコア0.75）。
2番目の候補者は、本の中で最高の候補者として認識されます（丸める前に、彼の評価は最初の候補者よりも高かった）。

ソース（NetBeans 6.9.1のプロジェクト）： ifolder.ru
パス：habrahabr.ru
念のため：実行可能.jarは\ dist \フォルダーにあります

Source: https://habr.com/ru/post/J136227/

More articles:


All Articles