
この記事は、コンピューターの多次元グラフィックスの基本的な数学的コンポーネントに精通することを目的としています。 この記事では、例としてSierpinski
シンプレックスを使用して、複雑な多次元の幾何学的形状の構築、移動、投影、表示の問題について説明します。
写真、ビデオ、ソースもあり、すべてが非常にシンプルで、読み、掘り下げられていることを保証します。
シェルピンスキーの三角形とは何か
、シェルピンスキーのピラミッドとは何なのか
が非常に明確です。 しかし、シェルピンスキーシンプレックスとは何ですか? まず、Wikiでシンプレックスの内容を読んでいない人のために、シンプレックスはn次元の四面体であると言います(
ビデオを参照)。 さて、シェルピンスキーシンプレックスは一種のフラクタルであり、三角形とシェルピンスキー四面体との類推によって構築されています。
等辺シンプレックスの構築
信じられませんが、これはこの記事にあるすべての中で最も難しいものです(私の推定によると)。 しかし、必要なのは、互いにおよび中心から等距離にあるn-1次元空間内のn個の点です。 さらに読む前に、そのようなポイントをどのように構築するかについて考えることを強くお勧めしますか?
もちろん、n> = 3の場合に興味があります。それ以外の場合は、単に面白くありません。 各n番目のポイントは、以前のすべてのポイントに基づいて構築されます。 開始するには、正三角形を規則的に作成する必要があります。
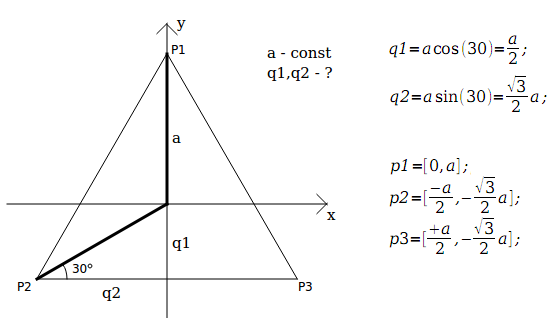
新しいポイントを追加するには、新しいディメンション(Wで表示)が必要です。 この測定を導入し、ポイントが他のすべてのポイントから等距離になるように、このポイントPnに対してW軸に沿ってq1を設定し、W軸に沿って他のポイントに-q2を設定します。 ポイントPnの残りの軸座標はゼロのままになります。 なに? すべてのポイントが-互いにおよび中心から等距離にあり、新しいポイントが他のすべてのポイントから等距離にあること。 このようなq1、q2を選択するだけで、すべてのポイントが互いに、また中心から等距離になるようになります。
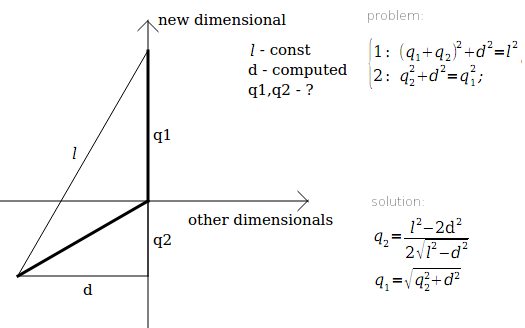
l-ポイント間の距離-常に、三角形の構築後に計算されます。
d-点から中心までの距離-変化し、新しい点を追加する前に計算されます。
最初の式は、受信したポイントから新しいポイントまでの距離が同じであることを示しています。
2つ目は、中心までの距離が同じであることです。
実際、このようにして、正反対のシンプレックスが得られます。
ソース:
double c = r * sqrt(3) / 2; double l = c * 2;
フラクタル
三角形(n = 2)とシェルピンスキー四面体(n = 3)の両方が、基本図形をn + 1と同じだがより小さいものに置き換えることにより、基本図形から作成されることは非常に簡単です。 新しい各図では、基本図の1つの点が基準として使用され、残りの点はこの点を含むセグメントの重心です。 原則として、すべてが非常にシンプルで明確です。
だから私たちは書く:
void rec(QVector<Simplex>& storage, const Simplex& current, int recursionDepth) { if (recursionDepth == maxRecursionDepth) storage.append(current); else { for (int i = 0; i <= n; i++) { Simplex newTriangle(current.dimensionsCount()); for (int k = 0; k <= n; k++) { if (i == k) newTriangle[k] = current[i]; else newTriangle[k] = (current[i] + current[k]) / 2.0; } rec(storage, newTriangle, recursionDepth + 1); } } }
ご覧のとおり、空間の次元に依存する場所は他になく、2Dと3Dの両方で正しく機能します。


回転と投影
回転するのは難しい場合があります(クォータニオン、マトリックス変換)が、それは単純に可能です...すべてを単純に行い、各2つの座標に沿って順番に回転します。 2Dの場合、これは点を中心とした回転、3Dの場合は直線、NDの場合は(N-2)次元空間の回転として理解できます。 実際、回転式は非常に簡単に計算されます:

まあ、それはプログラムするのがさらに簡単です:
for (int i = 0; i < coordinates.count(); i++) for (int k = i + 1; k < coordinates.count(); k++) { ratio = sqrt(2 + i * coordinates.count() + k); p1 = temp[i] * cos(angle * ratio) - temp[k] * sin(angle * ratio); p2 = temp[k] * cos(angle * ratio) + temp[i] * sin(angle * ratio); temp[i] = p1; temp[k] = p2; }
ここで、比率は係数であるため、異なる方向の回転は異なる速度で行われ、ループはありません。 temp [i]-現在の点のi番目の座標。
投影は、多次元空間で作業する最も難しい瞬間です。 多くの理由があります。
1.多次元の幾何学的オブジェクトの理解に誰も慣れていません。
2.物理学の光学系は、これについては沈黙しています(私の知る限り)。
3.たくさんの異なる方法と誰もが絵をオーバーロードし、何がより正確であるかは明確ではありません。
最も単純な方法-透視投影を使用します。 n次元の点を(n-1)空間に投影します。したがって、Nを下げるたびに、その点はすでに2次元または3次元であり、すでに表示できる点に到達します。
例として2Dから1Dを使用して、透視投影式を計算してみましょう。

2つの座標と一定の焦点を使用して、1つの座標を作成できることがわかります。 そして、式はコードのように非常に単純です:
for (int i = coordinates.count() - 1; i > 3; i--) for (int k = 0; k < i; k++) temp[k] *= focus / (focus + temp[i]);
これはどれくらい正しいですか? 一般的に、一度も、少しも、正しくありません! しかし、インターネット上にあるものから判断すると、非常に類似したものが他のプログラマーによって使用されています。 ここに、例えば、この投影法によって得られた
テセラクトがあります:

レンダリング
QPainterは最も簡単な方法です。開発環境の標準ツールを使用して、照明や三角形の塗りつぶしなどをせずに、通常の線ですべてを描画します。 私の情報源では、デフォルトでオンになっており、Qtがどこにいても機能します(Windows、Linux、Mac OSなど)。
実際、これはレンダリングコードの外観です。
QPoint center(this->width() / 2, this->height() / 2); foreach(const Simplex& simplex, simplexes) for (int i = 0; i < simplex.dimensionsCount() + 1; i++) for (int k = i+1; k < simplex.dimensionsCount() + 1; k++) p.drawLine(simplex[i].to2D(focus, angle) + center, simplex[k].to2D(focus, angle) + center);
ご覧のとおり、これ以上簡単なものはありません...しかし、私たちは美しくなければなりませんよね?
OpenGL 、
DirectXは、すべてをリアルタイムで美しくレンダリングできるプログレッシブメソッドです。 しかし、不幸があります:透明性なしでは美しいものはありません。これら2つのモンスターの透明性は、遠く(z->最大)から近く(z-> min)までレンダリングする必要があることを示唆しています。 このために、各フレーム、三角形を並べ替える必要があります。私の例では約6000です。問題は一般的な場合、どの三角形がより近く、どれがより遠くを判断できないことです。 さらに、多次元空間からの投影について話すとき、三角形が交差すると言います。 結果として、各反復をカットしてソートする必要がありますが、これはすでに非常に困難です...
このメソッドは実装しませんでした。
レイトレーシングは、医師が注文したものです。
このテクノロジーを使用すると、最高品質の画像を取得できますが、欠点は速度のみです。 しかし、実際には、リアルタイムは必要ありません。
トレースには、
POV-Rayを使用しました。これは、GUIがなくてもコマンドラインから実行できるという点でのみ、このタスクに理想的でした。
この奇跡を使用するために、プログラムが必要なポイントで満たす特定のテンプレートを作成しました。出力は、トレースの準備ができた.povファイルです。 ポイントのセットに基づくテンプレートは、三角形とフレームを構築し、その構造は非常に単純です。
#declare ppp = array[<<!!--count of points--!!>>] { <<!!--Main Array of points--!!>> }; #declare i = 0; #while(i < <<!!--count of points--!!>>) #if (vlength(ppp[i] - ppp[i+1])!=0) cylinder{ppp[i], ppp[i+1], 0.2 texture {pigment{color Gray}} } #end #if (vlength(ppp[i] - ppp[i+2])!=0) cylinder{ppp[i], ppp[i+2], 0.2 texture {pigment{color Gray}} } #end #if (vlength(ppp[i+1] - ppp[i+2])!=0) cylinder{ppp[i+1], ppp[i+2], 0.2 texture {pigment{color Gray}} } #end polygon {4 ppp[i], ppp[i+1], ppp[i+2] ,ppp[i] texture { Surface_Texture }} #declare i=i+3; #end
実際、このテンプレートに基づいて、1000枚の写真が異なる順番で作成され、その後、このビデオが作成されました。
ソースコードこの記事は、Fight with Fateのヘビーメタルチームの少女たちに捧げられています。