
むかしむかし、私がまだ素朴な少年だった頃、私は突然ひどく好奇心became盛になりました。 忠実なダイアルアップに乗って、インターネットで答えを探し始めたところ、興味のある情報のかなり詳細な説明を含む多くの記事を見つけました。 しかし、それらのどれも私には理解しやすいようには見えませんでした-コードリストは中国人のようで、珍しい用語やさまざまな式を理解しようとする試みは失敗しました。
したがって、この記事の目的は、最も単純な圧縮アルゴリズムのアイデアを、知識や経験がまだ専門的な文献をすぐに理解できない、またはプロファイルがそのようなトピックから完全に遠い人に与えることです。 つまり いくつかの最も単純なアルゴリズムについて「すぐに」話して、キロメートルコードリストなしでの実装例を示します。
エンコードプロセスの実装の詳細や、文字列の出現の効率的な検索などのニュアンスは考慮しないことをすぐに警告します。 この記事では、アルゴリズム自体とそのアルゴリズムの結果を表示する方法のみを扱います。
RLE-コンパクトな均一性
RLEアルゴリズムはおそらく最も単純なものです。その本質は、繰り返しをエンコードすることです。 言い換えれば、同一の要素のシーケンスを取り、それらを数量/値のペアに「崩壊」させます。 たとえば、「AAAAAAAABCCCC」のような文字列は、「8×A、B、4×C」のようなレコードに変換できます。 一般に、アルゴリズムについて知っておく必要があるのはこれだけです。
実装例
0から255までの値を取ることができる整数係数のセットがあるとします。論理的に、このセットをバイトの配列として保存するのが妥当であるという結論に達しました。
unsigned char data[] = { 0, 0, 0, 0, 0, 0, 4, 2, 0, 4, 4, 4, 4, 4, 4, 4, 80, 80, 80, 80, 0, 2, 2, 2, 2, 255, 255, 255, 255, 255, 0, 0 };
多くの人にとって、このデータを16進ダンプとして見る方がはるかに馴染みがあるでしょう:
0000: 00 00 00 00 00 00 04 02 00 04 04 04 04 04 04 040010: 50 50 50 50 00 02 02 02 02 FF FF FF FF FF 00 00考えて、スペースを節約するために何らかの方法でそのようなセットを圧縮するのが良いと判断しました。 これを行うために、我々はそれらを分析し、パターンを明らかにしました。同じ要素からなるサブシーケンスに出くわすことが非常に多いです。 もちろん、RLEはこれにぴったりです!
新たに得られた知識を使用してデータをエンコードします:6×0、4、2、0、7×4、4×80、0、4×2、5×255、2×0
コンピュータフレンドリーな方法で何らかの形で結果を提示する時が来ました。 これを行うには、データストリームで、エンコードされたチェーンからシングルバイトを何らかの方法で分離する必要があります。 バイト値の範囲全体がデータで使用されるため、目的に合わせて値の範囲を選択することは不可能です。
この状況から抜け出すには、少なくとも2つの方法があります。
- 圧縮チェーンのインジケータとして、1バイトの値を選択し、実際のデータと競合する場合は、それらをスクリーニングします。 たとえば、「公式」の目的で値255を使用する場合、入力でこの値が満たされると、「255、255」を記述し、インジケータの後に最大254を使用するように強制されます。
- 繰り返されるだけでなく、後続の単一要素の数を示す、エンコードされたデータを構造化します。 そうすれば、データがどこにあるかを事前に知ることができます。
私たちの場合の最初の方法は効果的ではないようですので、おそらく、2番目の方法に頼るでしょう。
したがって、2つのタイプのシーケンスがあります。単一要素のチェーン(「4、2、0」など)と同一要素のチェーン(「0、0、0、0、0、0」など)です。 「サービス」バイトで、シーケンスタイプに1ビットを選択します:0 —単一要素、1 —同一。 これには、たとえば、バイトの最上位ビットを使用します。
残りの7ビットには、シーケンスの長さを格納します。 エンコードされたシーケンスの最大長は127バイトです。 公式のニーズに合わせて2バイトを割り当てることができますが、この場合、このような長いシーケンスは非常にまれなので、単純に短いシーケンスに分割する方が簡単で経済的です。
出力ストリームでは、最初にシーケンスの長さを書き込み、次に1つの繰り返し値または指定された長さの非繰り返し要素のチェーンを書き込みます。
最初に注目すべきこと-この状況では、未使用の値がいくつかあります。 長さがゼロのシーケンスは存在できないため、最大長を128バイトに増やし、エンコード中に長さから1を引き、デコード中に追加できます。 したがって、0〜127の長さの代わりに1〜128の長さをエンコードできます。
2番目に気付くことは、単位長の同一要素のシーケンスがないことです。 したがって、エンコード中にそのようなシーケンスの長さの値からもう1単位を差し引くことにより、それらの最大長を129に増やします(単一要素のチェーンの最大長は依然として128に等しい)。 つまり 同一の要素のチェーンの長さは2〜129です。
データを再びエンコードしますが、コンピューターに優しい方法でエンコードします。 オーバーヘッドバイトを[T | L]として書き込みます。ここで、Tはシーケンスのタイプ、Lは長さです。 変更された形式で長さを記述することをすぐに考慮します。T= 0ではLから1を引き、T = 1では2を取ります。
[1 | 4] 、0、
[0 | 2] 、4、2、0、
[1 | 5] 、4、
[1 | 2] 、80、
[0 | 0] 、0、
[1 | 2] 、 2、
[1 | 3] 、255、
[1 | 0] 、0
結果をデコードしてみましょう:
- [1 | 4] 。 T = 1、次のバイトはL + 2(4 + 2)回繰り返されます:0、0、0、0、0、0
- [0 | 2] 。 T = 0なので、L + 1(2 + 1)バイトを読み取ります:4、2、0
- [1 | 5] 。 T = 1、次のバイトを5 + 2回繰り返します:4、4、4、4、4、4、4、4、4。
- [1 | 2] 。 T = 1、次のバイトを2 + 2回繰り返します:80、80、80、80。
- [0 | 0] 。 T = 0、読み取り0 + 1バイト:0
- [1 | 2] 。 T = 1、バイト2 + 2を繰り返します:2、2、2、2。
- [1 | 3] 。 T = 1、バイト3 + 2を繰り返します:255、255、255、255、255。
- [1 | 0] 。 T = 1、バイト0 + 2を繰り返します:0、0。
そして今、最後のステップ:結果をバイトの配列として保存します。 たとえば、バイトでパックされたペア
[1 | 4]は次のようになります。
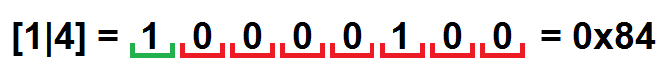
その結果、次の結果が得られます。
0000:
84 00
02 04 02 00
85 04
82 80
00 00
82 02
83 FF
0010:
80 00
したがって、この入力データの例では、簡単な方法で18バイト18が得られました。特に、より長いチェーンではるかに優れていると考えると、良い結果になります。
可能な改善
アルゴリズムの有効性は、アルゴリズム自体だけでなく、その実装方法にも依存します。 したがって、さまざまなデータに対して、さまざまなコーディングのバリエーションとエンコードされたデータの表現を開発できます。 たとえば、画像をエンコードする場合、可変長のチェーンを作成できます。長いチェーンを示すために1ビットを選択し、1に設定されている場合は、次のバイトにも長さを格納します。 そのため、短いチェーン(129ではなく65要素)の長さを犠牲にしますが、わずか3バイト(2
14 + 2)で最大16385要素の長さのチェーンをエンコードする機会を与えます!
ヒューリスティックなコーディング手法を使用することにより、さらなる効率を達成できます。 たとえば、「ABBA」という方法で次のチェーンをコーディングします。 "
[0 | 0] 、A、
[1 | 0] 、B、
[0 | 0] 、A"を取得します-つまり、 4バイトを6バイトに変換して、ソースデータを1.5倍に膨らませました! そして、そのような短い交互の異種シーケンスが多ければ多いほど、データがより冗長になります。 これを考慮すると、結果を「
[0 | 3] 、A、B、B、A」としてエンコードできます-余分なバイトを1つだけ使用します。
LZ77-繰り返しの簡潔さ
LZ77は、LZファミリーで最も単純で最も有名なアルゴリズムの1つです。 作成者に敬意を表して名付けられた:アブラハムレンペル(アブラハム
Lエンペル)とヤコブジヴァ(ヤコブ
Z iv)。 タイトルの77という数字は1977年を意味し、このアルゴリズムについて説明した記事が出版されました。
基本的な考え方は、要素の同じシーケンスをエンコードすることです。 つまり、入力で要素のチェーンが複数回発生した場合、それ以降のすべての要素は、その最初のインスタンスへの「リンク」に置き換えることができます。
このファミリーのファミリーの他のアルゴリズムと同様に、LZ77は以前に遭遇したシーケンスを保存する辞書を使用します。 これを行うために、彼はいわゆるの原則を適用します 「スライディングウィンドウ」:常に現在のコーディング位置の前にある領域。この領域内でリンクをアドレス指定できます。 このウィンドウは、このアルゴリズムの動的辞書です。ウィンドウ内の各要素には、ウィンドウ内の位置と長さの2つの属性があります。 物理的な意味では、これはすでにエンコードしたメモリの一部にすぎません。

実装例
それでは、何かをエンコードしてみましょう。 このために適切な文字列を生成します(その不合理さを事前に謝罪します):
「圧縮と解凍により印象が残ります。 ははははは!」
メモリ内での表示方法は次のとおりです(ANSIエンコード):
0000: 54 68 65 20 63 6F 6D 70 72 65 73 73 69 6F 6E 20 The compression0010: 61 6E 64 20 74 68 65 20 64 65 63 6F 6D 70 72 65 and the decompre0020: 73 73 69 6F 6E 20 6C 65 61 76 65 20 61 6E 20 69 ssion leave an i0030: 6D 70 72 65 73 73 69 6F 6E 2E 20 48 61 68 61 68 mpression. Hahah0040: 61 68 61 68 61 21 ahaha!ウィンドウのサイズはまだ決定していませんが、エンコードされた文字列のサイズよりも大きいことに同意します。 文字の重複チェーンをすべて見つけてみましょう。 チェーンは、1つより長い文字のシーケンスです。 チェーンがより長い繰り返しチェーンの一部である場合、無視します。
「圧縮とt
[he] de
[compression]は
[an] i
[mpression]のままです。
ハハ[ahahaha] !”
より明確にするために、繰り返されたシーケンスとそれらの最初の出現の対応が見える図を見てみましょう:

文字列「ahahahaha」が短いチェーン「ah」に対応するため、ここでの唯一の不明瞭な点は、おそらく「Hahahahaha!」というシーケンスです。 しかし、ここでは珍しいことは何もありません。RLEで前述したように、アルゴリズムがときどき機能するようにする手法を使用しました。
実際には、展開するときに、指定された数の文字を辞書から読み取ります。 そして、シーケンス全体が周期的であるため、つまり その中のデータは一定の周期で繰り返され、最初の周期のシンボルは展開位置の直前にあります。それから、前の周期のシンボルを次の周期にコピーするだけで、それらからチェーン全体を再作成できます。
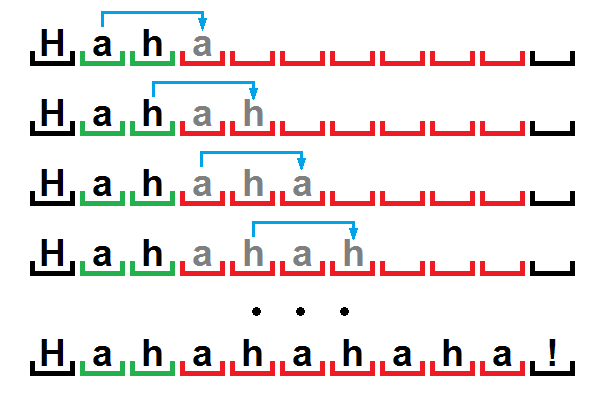
私たちはそれを理解しました。 次に、見つかった繰り返しを辞書への参照に置き換えます。 リンクを[P | L]形式で記録します。ここで、Pは文字列内で最初に出現するチェーンの位置、Lはその長さです。
「圧縮とt
[22 | 3] de
[5 | 12]は
[16 | 3] i
[8 | 7]のままになります。 ハ
[61 | 7] !”
しかし、スライディングウィンドウを扱っていることを忘れないでください。 理解を深めるために、リンクがウィンドウのサイズに依存しないように、絶対位置をそれらと現在のコーディング位置との差に置き換えます。
「圧縮とt
[20 | 3] de
[22 | 12]は
[28 | 3] i
[42 | 7]のままになります。 ハハ
[2 | 7] !”
ここで、現在のエンコード位置からPを減算して、文字列内の絶対位置を取得するだけです。
今度は、ウィンドウのサイズとエンコードされたフレーズの最大長を決定します。 テキストを扱っているので、特に長い繰り返しシーケンスが含まれる場合はまれです。 そのため、長さとして4ビットを選択しましょう-一度に15文字の制限で十分です。
ただし、同じチェーンをどれだけ深く探すかは、ウィンドウのサイズに依存します。 小さなテキストを扱っているので、使用するビット数を最大2バイトで補うのがちょうどいいでしょう。このために12ビットを使用して、4096バイトの範囲のリンクをアドレス指定します。
RLEの経験から、すべての値を使用できるわけではないことがわかります。 明らかに、リンクの最小値は1です。したがって、1..4096の範囲で逆方向にアドレスを指定するには、エンコード時にリンクから1を減算し、デコード時に加算する必要があります。 シーケンスの長さも同じです。0..15の代わりに範囲2..17を使用します。ゼロの長さでは機能せず、個々の文字はシーケンスではないためです。
これらの修正を加えたエンコードされたテキストを想像してください。
「圧縮とt
[19 | 1] de
[21 | 10]は
[27 | 1] i
[41 | 5]のままになります。 ハハ
[1 | 5] !”
ここでも、圧縮されたチェーンを他のデータから何らかの形で分離する必要があります。 最も一般的な方法は、構造を再度使用し、データが圧縮されている場所と圧縮されていない場所を直接示すことです。 これを行うには、エンコードされたデータを8つの要素(文字またはリンク)のグループに分割し、これらの各グループの前に、各ビットが要素のタイプに対応するバイトを挿入します:文字の場合は0、リンクの場合は1です。
グループに分けます:
- 「コンプ」
- 「Ression」
- 「そしてt [19 | 1] de」
- " [21 | 10] leave [27 | 1] "
- 「私[41 | 5] 。 ハ[2 | 5] »
- 「!」
グループを構成します:
"
{0,0,0,0,0,0,0,0,0} comp
{0,0,0,0,0,0,0,0,0,0} 解像度{0,0,0,0,0,0,1 、0,0}およびt
[19 | 1] de
{1,0,0,0,0,0,0,1,0} [21 | 10] leave
[27 | 1] {0,1,0,0、 0,0,0,1} i
[41 | 5] 。 ハハ
[1 | 5] {0} !”
したがって、アンパック中にビット0が見つかった場合、文字を出力ストリームに読み込むだけで、ビット1であればリンクを読み取り、リンクを読み取ることで辞書からシーケンスを読み取ります。
結果をバイトの配列にグループ化するだけです。 ビットとバイトを最高から最低の順に使用することに同意しましょう。 例
[19 | 1]を使用して、リンクがどのようにバイトにパックされるかを見てみましょう。

その結果、圧縮ストリームは次のようになります。
0000:
00 54 68 65 20 63 6f 6d 70
00 72 65 73 73 69 6f#コンプ#ressio
0010:6e 20
04 61 6e 64 20 74
01 31 64 65
82 01 5a 6c n #and t ## de ### l
0020:65 61 76 65
01 b1 20
41 69
02 97 2e 20 48 61 68軒###i ##。 うん
0030:
00 15 00 21
00 00 00 00 00 00 00 00 00 00 00 00 00 ###!
可能な改善
基本的に、RLEについて説明したことはすべてここで当てはまります。 特に、コーディングにおけるヒューリスティックアプローチの有用性を示すために、次の例を検討してください。
「長いgoooooong。 すごいバウンド。」
「loooooower」という単語のシーケンスのみを検索します。
「長いgoooooong。
[lo] [ooooo] werバウンド。」
このような結果をエンコードするには、リンクごとに4バイトが必要です。 ただし、そうする方が経済的です。
「長いgoooooong。 l
[oooooo] wer bound。”
次に、1バイトを節約します。
結論の代わりに
シンプルでありながら、あまり効率的ではないように見えますが、これらのアルゴリズムはIT分野のさまざまな分野でまだ広く使用されています。
それらのプラスは単純さと速度であり、より複雑で効率的なアルゴリズムは、その原則とその組み合わせに基づいています。
このように記述されたこれらのアルゴリズムの本質が、誰かが基本を理解し、より深刻なことの方向に目を向け始めるのに役立つことを願っています。