永続的なカットツリー

はじめに

データ構造は、 一時 （ 一時 ）と永続 （ 永続 ）の2つのグループに分けることができます。

エフェメラルは、最新バージョンのみを保存するデータ構造です。
永続構造、つまり以前のバージョンをすべて保持する構造は、2つのサブグループに分けることができます：データ構造で最新バージョンのみを変更できる場合、 部分永続と呼ばれますが、バージョンの変更が許可されている場合、そのような構造は完全に永続的と考えられます。

次に、セグメントのツリーとその完全に永続的なバージョンが考慮されます。
すべてのコードはGitHubで入手できます 。

ラインツリー

セグメントのツリーにすでに精通している人は、 永続バージョンのセクションにすぐに行くことができます。

セグメントツリーは、特定の配列Aに対して次の操作をすばやく実行できるデータ構造です。

• Change(i, x) A[i]値をChange(i, x)変更します
• F(i, j) f(A[i], A[i + 1], ..., A[j])計算f(A[i], A[i + 1], ..., A[j])

両方の操作はO（log n）で実行されます。 f関数としてfしばしば合計、最小、または最大を取ります。

説明

nを配列A長さとすると、その長さが2の累乗に等しくなるまで中立要素で埋めます（たとえば、 fが合計の場合、配列はゼロで補われます）。

ここで、 Aすべての要素が葉であり、すべての葉の深さが同じで、子頂点の値からのf値が他のすべての頂点に格納されるようなバイナリツリーを構築します。

例として、配列A = [4, 1, 4, 2, 5, 3] 4、1、4、2、5、3]のセグメントツリーを考えA = [4, 1, 4, 2, 5, 3] 。


このようなツリーをバイナリヒープとして保存すると便利です。頂点の配列として、上から下へ左から右へと連続して記述されます。

  19 11 8 5 6 8 0 4 1 4 2 5 3 0 0 

この場合、インデックスi頂点の場合、その祖先は頂点((i - 1) / 2)になり、左右の子頂点にはそれぞれインデックス(2 * i + 1)と(2 * i + 2)割り当てられます（仮定）配列内の要素には最初から番号が付けられていること）。

建物

セグメントのツリーを上から下に再帰的に構築すると便利です。各頂点について、左右の子頂点を構築し、その値からfの値を計算します。シートの場合、対応する配列値をツリーに書き込むだけです。

このような方法でツリーを構築すると、各頂点が1回訪問されます。また、ツリー内の頂点の数はΘ（n）であるため、構築の複雑さもΘ（n）です。

変更

要素の値が変更された後、この要素の祖先の値の一部がツリー内で劣化した可能性があります。 これを修正するには、この要素の祖先の値を再カウントし、ツリーを下から上に登っていきます。

たとえば、配列A A[3]を10に置き換えると、値6、11 11および19の頂点が再計算されます。

ツリーの高さはlog nであるため、変更操作は正確にlog nの頂点に影響を与えるため、操作の漸近的な動作はO（log n）です。

Fの計算

この操作は、上から下に再帰的に実行されます。

任意の頂点v F範囲l..rに対して計算されると仮定すると、 l..((l + r) / 2)の値F l..((l + r) / 2)左ドーター頂点で計算され、 ((l + r) / 2 + 1)..r 。

要求F(i, j)到着し、現在の頂点がvます。 次の2つのケースが考えられます。

• ノードvでは、値F(i, j)はすでに計算されています。 その場合、要求に対する答えは頂点v値になります。
• ノードvでは、 Fより大きな範囲に対して書き込まれます。 この場合、左の子頂点に対して計算F(i, (l + r) / 2)を呼び出し、右の子頂点に対してF((l + r) / 2 + 1, j)を再帰的に呼び出します。答えはこれら2つの値からfです。

例

C ++での行ツリーの実装 。

永続的な回線ツリー

永続化はさまざまな方法で実現できますが、最も簡単なのは古いバージョンの完全なコピーを作成し、変更ごとにセグメントの通常のツリーのように変更することです。ただし、この方法はメモリを大量に消費し、 Change操作の漸近的な動作をO（n）に悪化させます。

建物

セグメントの永続的なツリーの構築は、セグメントの通常のツリーの構築に似ていますが、各頂点に対して、子頂点への参照を明示的に保存する必要がある点が異なります。
さらに、対応するバージョンのツリーのルートである頂点の配列を保存する必要があります。 構築時に、単一の頂点が追加されます。これは、結果のツリーのルートです。



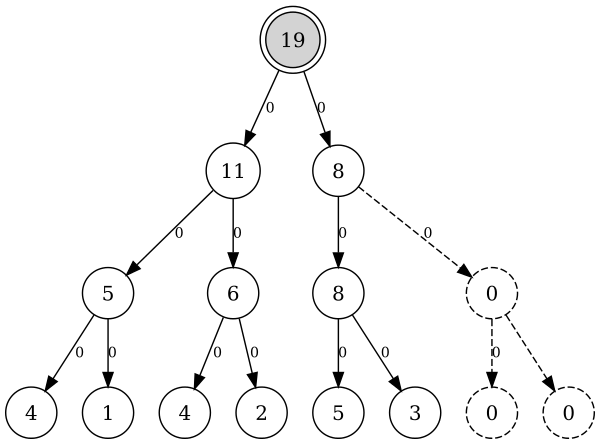
セグメントの一時的なツリーと比較した場合の唯一の変更は、左右の子頂点に関する情報の追加であるため、構造の複雑さは変わらず、つまりΘ（n）です。

変更

頂点を変更するときにツリーを完全にコピーする代わりに、変更されるはずの頂点のみが追加され、古い頂点の値を変更する代わりに、再計算された値が新しいものに保存されます。 すべての新しい頂点は、古いバージョンツリーの1つの頂点と、追加したばかりの頂点の1つを参照します。

新しいブランチの追加は、ツリー全体の構築と同じ方法で行われますが、2つの子頂点を構築する代わりに、変更された頂点が存在する方向にのみ新しい頂点が構築されます。
その後、ルート頂点の配列が更新されます。



変更ではlog nの頂点のみが追加されるため、操作の漸近的な動作はO（log n）です。

Fの計算

Fの計算は、一時的なツリーに似ています。 唯一の違いは、子ノードへの移行と異なるルートノードからの起動です。
これは、O（log n）の複雑さを意味します。

例

C ++でのセグメントの永続的なツリーの実装 。

タスク

セグメントの永続的なツリーを使用して、「 ロールバック 」 タスクを解決できます （ タスク解析 ）。 セグメントの永続的なツリーの上記の実装を使用した問題の解決策は、 GitHubで利用できます 。
また、範囲に関するk番目の順序統計の問題の説明を読むことができます。