オリジナルでは、名前は「平均評価でソートしない方法」のように聞こえます。 「平均評価で並べ替えない」という文字通りの翻訳は不明瞭で、記事の内容をより悪く反映すると考えました。
問題文
Webプログラミングを行います。 サイトのコンテンツを評価するユーザーがいます。 高評価のコンテンツを上部に、低評価のコンテンツを下部に配置します。 これを行うには、ユーザーの評価に基づいて、特定の「評価」を計算する必要があります。
間違った決定No. 1
= ( ) - ( )
なぜ間違っているのですか。 単一のオブジェクトに600の肯定的な評価と400の否定的な評価があるとします。 その結果、60%が肯定的です。 さらに、他のオブジェクトが5500の正の評価と4500の負の評価を持っていると仮定します。 その結果、55%が肯定的です。 このアルゴリズムは、2番目のオブジェクト(評価は1000ですが、正の評価は55%のみ)を最初のオブジェクト(200の評価と正の評価は60%)の上に配置します。
間違っています。
この間違いを犯すサイト :
Urban Dictionary
間違った決定No. 2
= = ( ) / ( )
なぜ間違っているのですか。 常に多くの評価がある場合、平均評価はうまく機能します。 しかし、1つのオブジェクトに2つの正の評価と0の負の評価があるとします。 さらに、2番目のオブジェクトに100の正の評価と1つの負の評価があるとします。 このアルゴリズムは、最初のオブジェクト(非常に少数の肯定的な評価)の下に(多数の肯定的な評価を持つ)2番目のオブジェクトを配置します。
これは間違っています。
この間違いを犯すサイト :
Amazon
正しい決断
= (Wilson)
なぜこれが正しいのですか。 正の推定値のシェアと少数の観測値の不確実性とのバランスを見つける必要があります。 幸いなことに、この問題を解決するための数学的装置は、1927年にエドウィンウィルソンによって開発されました。 私たちは次のことを知りたいと思っています。「評価するためのデータのセットを持っているので、95%の確率で、ポジティブな評価の「本当の」シェアとは何ですか?」 ウィルソンは答えを与えます。 ポジティブとネガティブの評価のみが与えられた場合(つまり、5段階の評価システムを考慮しない場合)、ポジティブ評価のシェアの下限は次の式で計算されます:
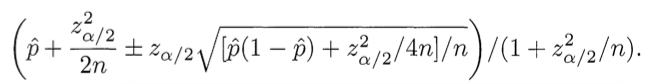
マイナスを使用して、プラス/マイナスが書き込まれ、下限を計算します。 ここで、
p̂は正の推定値の割合、zα
/ 2は標準正規分布の分位数
* (1-α/ 2)、
nは推定値の総数です。 Rubyに適用される同様の式:
*数学的統計の変位値は、特定の確率変数が一定の確率で超えない値です。 ウィキペディア
require 'statistics2' def ci_lower_bound(pos, n, confidence) if n == 0 return 0 end z = Statistics2.pnormaldist(1-(1-confidence)/2) phat = 1.0*pos/n (phat + z*z/(2*n) - z * Math.sqrt((phat*(1-phat)+z*z/(4*n))/n))/(1+z*z/n) end
ここで、
posは正の評価の数、
nは評価の合計数、そして
信頼度は統計的に信頼度のレベルを設定します:0.95に設定して、95%の下限の正確性を0.975で数える確率で97.5%の確率を設定します。 この関数の番号zは変更されません。 統計データを操作するのに便利なソフトウェアがない場合、またはパフォーマンスが重要な場合は、zの値をいつでもハードコーディングできます。 (0.95の信頼レベルには1.96を使用します)。
以下に、必要なことを行うSQLクエリを示します。 正と負の評価を持つオブジェクトのテーブルがあり、95%信頼区間の下限で並べ替えることを想定しています。
SELECT widget_id, ((positive + 1.9208) / (positive + negative) - 1.96 * SQRT((positive * negative) / (positive + negative) + 0.9604) / (positive + negative)) / (1 + 3.8416 / (positive + negative)) AS ci_lower_bound FROM widgets WHERE positive + negative > 0 ORDER BY ci_lower_bound DESC;
このような複雑なSQLクエリが有用な結果を返すことができると信じていない場合は、この結果を上記の他の2つの方法の結果と比較してください。
SELECT widget_id, (positive - negative) AS net_positive_ratings FROM widgets ORDER BY net_positive_ratings DESC;
SELECT widget_id, positive / (positive + negative) AS average_rating FROM widgets ORDER BY average_rating DESC;
ごくわずかな追加の数学で優れたコンテンツがポップアップすることがすぐにわかります。 ただし、大規模なデータベースでこのSQLクエリを実行する前に、適切なテーブルのインデックス作成について、使いやすい管理者に相談してください。 当初、私は教師の1人に敬意を表し
てチャック・ノリスに関するファクトジェネレーターのためにこのメソッドを開発しましたが、このメソッドは
Reddit 、
Yelp 、
Diggなどの場所でテストされました。
メソッドの他のアプリケーション
ウィルソンの信頼区間は、並べ替えだけでなく適用できます。
特定の行為をしている人の割合を確実に知りたいどこでも使用できます。 たとえば、次の目的に使用できます。
- スパムまたは悪用を特定します。 メッセージを見た人のうち何人がスパムとしてマークしますか?
- 「最高」のリストを作成します。 メッセージを見た人のうち何人が「最高」とマークしますか?
- 「最も共有されている」リストの作成。 メッセージを見た何人が「共有」ボタンをクリックしますか?
この方法は、評価の総数に対する肯定的な評価の数に関する結論よりも、ビューの数、ダウンロードの数、または購入の数に関して「最高」のリストを作成するのにはるかに役立ちます。 平凡なものを発見した多くの人々は、まったく投票することを気にしません。 その後の投票なしで何かを表示または購入するという単なる事実には、オブジェクトの品質に関する有用な情報が含まれています。
参照資料
- 二項比例信頼区間(Wikipedia)
- Agresti、Alan、Brent A. Coull(1998)、「二項比率の区間推定では「近似」は「正確」よりも優れている」、The American Statistician、52、119-126。
- ウィルソン、EB(1927)、「推定、継承の法則、および統計的推論」、Journal of the American Statistical Association、22、209-212。
私からのPS
翻訳自体は私が行ったものではありません。
karabozに感謝し
ます 。
数学用語の翻訳の正確性について完全に確信はありません
が、説明に感謝します!
当初、Facebookで
元の記事に関する議論が起こりました。 オーバーロードされた記事に挿入しなかったコメントには興味深いことがあります。
しおり
Habrで10回読むよりも1回見やすくするために、Habrで説明した方法を使用してコメントを並べ替えるブックマークレットをいくつか作成し、Dar〜Darの
ブログを95%の精度で作成しました。 Chrome / Safariでのみ確認しました:
javascript:jQuery.getScript('http://dl.dropbox.com/u/285016/code/habr_comment_by_rating.js');
javascript:jQuery.getScript('http://dl.dropbox.com/u/285016/code/dd_comment_by_rating.js');
次のようになります(クリック可能):
JavaScript評価の実装
以下の機能では、単一の肯定的な投票を受け取っていない処理済みオブジェクトが追加処理されます。 この場合、マイナスの数が返されます。 それ以外の場合、評価は[0; 1)の範囲になります。 賛成票と反対票の数がパラメータとして渡されます。
function wilson_score(up, down) { if (!up) return -down; var n = up + down; var z = 1.64485;
PPS
数式を任意の投票スケールに適合させました。 Pythonコード:
def wilson_score(sum_rating, n, votes_range = [0, 1]): z = 1.64485 v_min = min(votes_range) v_width = float(max(votes_range) - v_min) phat = (sum_rating - n * v_min) / v_width / float(n) rating = (phat+z*z/(2*n)-z*sqrt((phat*(1-phat)+z*z/(4*n))/n))/(1+z*z/n) return rating * v_width + v_min
ここで、
sum_ratingはすべての投票の合計、
nは数値、
votes_rangeは可能な評価の範囲です。 戻り値は、votes_rangeの指定範囲内にあります。