以前の出版物の人気の低下は、人気をサポートするための行動を促しています。 最初の出版物の人気は、その後の出版物よりもかなり高いことに気付きました。 再起動を試みます。
前のシリーズでは、SVDメソッドを慎重に検討し、さらにプログラムコードに取り入れました。 このテキストから始めて、より一般的なことを検討します。 もちろん、これらのことは常にレコメンダーシステムと密接に関連しており、レコメンダーシステムでどのように発生するかについて説明しますが、機械学習のより一般的な概念に焦点を当てます。 今日は過剰適合と正則化についてです。

私は古典から始めますが、これからもそれほど明らかにならない例です。 Rを開いて(誰も知らない場合、
Rは、あらゆる種類の統計、機械学習、およびデータ処理全般に世界で最も優れたツールの1つです。私はそれを強くお勧めします)、自分用にある種のシンプルで小さなデータセットを生成します。 単純な3次多項式を取ります
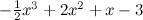
そして、そのポイントに正規分布ノイズを追加します。
> x <- c(0:6) / 2 > y_true <- -.5*x^3 + 2*x^2 + x – 3 > err <- rnorm( 7, mean=0, sd=0.4 ) > y <- y_true + err > y [1] -2.3824664 -2.1832300 -0.7187618 1.7105423 2.1338531 4.7356023 5.0291615
これで、これらのポイントを完全な曲線で一緒に描くことができます。
> curve(-.5*x^3 + 2*x^2 + x - 3, -1, 4, ylim=c(-5,6) ) > points(x, y, pch=21, bg="red")
図のようになります。

次に、このデータから多項式を訓練してみましょう。 多項式からの点の二乗偏差の合計を最小化します(最も一般的な古典回帰を行います)。つまり、最小化する多項式p(x)を探します。

。
もちろん、Rではこれは1つのチームによって行われます。 まず、線形多項式をトレーニングして描画します。
> m1 <- lm ( y ~ poly(x, 1, raw=TRUE) ) > pol1 <- function(x) m1$coefficients[1] + m1$coefficients[2] * x > curve(pol1, col="green", lwd=2, add=TRUE)
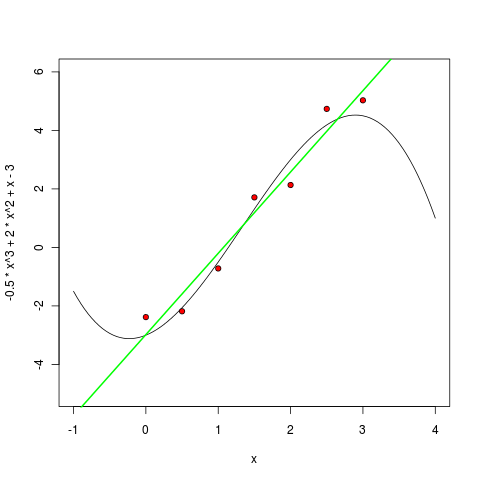
次に、2次の多項式:
> m2 <- lm ( y ~ poly(x, 2, raw=TRUE) ) > pol2 <- function(x) m2$coefficients[1] + m1$coefficients[2] * x + m1$coefficients[3] * (x^2) > curve(pol2, col="blue", lwd=2, add=TRUE)
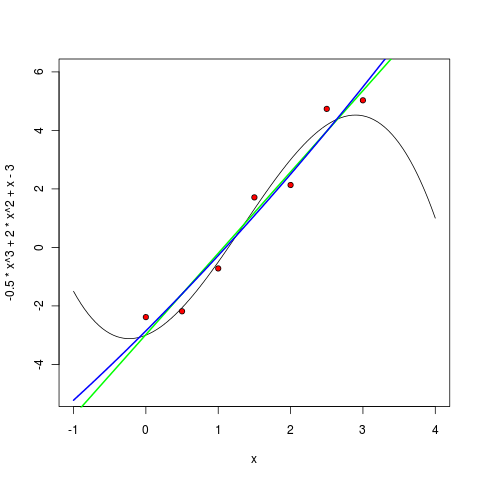
3次多項式は、予想どおり、すでに非常に類似しています。

しかし、さらに学位を上げるとどうなりますか? 実際には、結局のところ、「多項式の真の次数」、つまり モデルの真の複雑さ。 モデルを複雑にするにつれて、利用可能なポイントを近似することはより良くなり、結果はますます良くなり、モデルを訓練するだけでますます難しくなります。 これが本当にそうかどうか見てみましょう。
5次多項式はすでに非常に疑わしいように見えます-もちろん、ポイント間でもうまく動作しますが、このモデルによる外挿が適切でないことは既に明らかです-ポイントが終了するとすぐに無限に行き過ぎます。
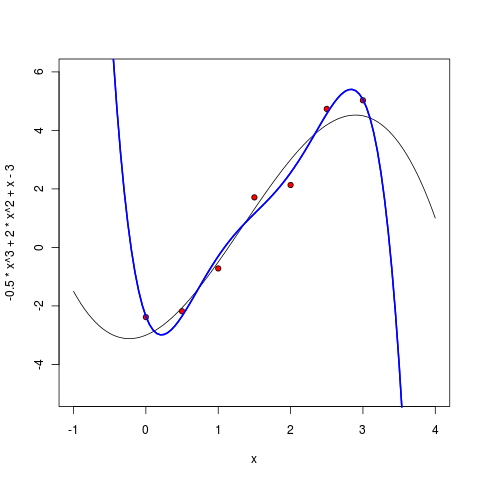
6度から始めて、私たちのアプローチの間違いなく壮大な失敗を見る。 最小化したいエラーは厳密にゼロに等しくなりました-結局、6次の7点多項式を介して正確に描くことができます! しかし、ここでは、結果として得られるモデルの利点は、おそらく厳密にゼロに等しくなります。現在、多項式は、既存のポイントの限界を超えて不十分に外挿するだけでなく、それらの間を非常に奇妙に補間するだけでなく、ポイントから期待するのが難しい局所的な極値まで実行します。
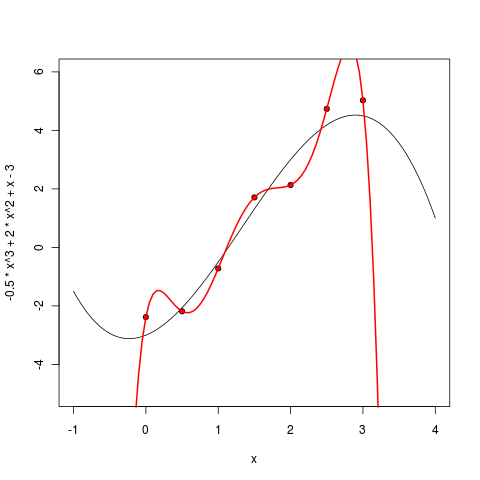
どうしたの? 機械学習で発生したことを「過剰適合」と呼びます。パラメーターが多すぎるモデルを使用し、そのモデルはデータから十分に訓練されており、最も重要なのは予測力に反しています。
どうする? 次のシリーズでは、これをより概念的にどのように行うことができるかを説明しますが、ここでそれを信じてみましょう。この場合の過剰適合は、結果の多項式が大きすぎる係数であるという事実に現れます。 たとえば、ここでトレーニングした3次多項式を示します。
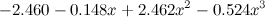
、
そして、ここで-違いを感じる-第六度:
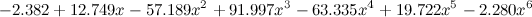
。
したがって、かなり自然な方法でこれに対処できます。目的関数にペナルティを追加するだけで、大きすぎる係数に対してモデルが罰せられます。
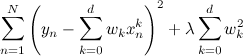
。
このような過剰適合は、SVDで発生させた場合に常に発生します。 実際、ファクターの数に等しい無料のパラメーターの数(つまり、少なくとも数個、またはおそらく数十個)を各ユーザーおよび各製品に導入します。 したがって、正則化のないSVDはまったく適用できません-もちろん、よく学習しますが、予測のためには、ほとんど実用的ではありません。
SVDのレギュレーターは、通常の回帰の場合とまったく同じように機能します。ペナルティを追加します。これは、係数サイズが大きいほど大きくなります。
前のシリーズの1つで、私はすぐに正則化者とともに目的関数を書きました。
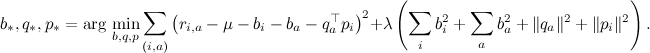
勾配上昇式がそこに与えられます-係数λはそれらの正則化に責任があります。
しかし、これはかなり不思議に見えますが、なぜ大きな係数は小さな係数よりも突然悪いのでしょうか? 将来的には、より概念的な
ベイジアン側からこの問題をどのように見ることができるかについてお話します。