こんにちは、Habr。
最近、たまたま彼が古いリセウムで、なぜ数学を勉強しているのか、あとでそれを応用して何ができるのかというトピックについて講演をしたことがありました。 10年生の小学生にとっては、おそらく少し複雑であることが判明しました。 このトピックがhabrasocietyの誰かにとって興味深いものになることを願っています(ここで紹介するオプションはLyceumで読んだものよりも少し複雑ですが、これは問題だとは思いません)。
だから。 特に、画像処理に焦点を当てます。これは、説明の観点から最も単純ですが美しい画像のノイズを抑制する方法の1つです。
少し前に、画像処理の物理学の大きさを自分で発見しました。 私はこれに非常に興味がありました。科学のこれらの2つの分野が私の頭の中で交わることはなかったからです。 この記事では、平面上の物質移動の問題を解決することにより、画像からノイズを除去する方法を紹介します。
画像表示
最初に、イメージと見なすものを明確にします。 説明を簡単にするために、ここではb / wの発明のみを検討します。
それらを飽和のマトリックスとして表します。

したがって、画像の各ピクセルは行列要素に対応します。 行列の値は、区間
[0,255] float数です。
いくつかの画像を取り、それにノイズを追加します(異なるノイズ強度を設定することでアルゴリズムがノイズにどれだけうまく対処できるかを確認できるため、これは既にノイズのある画像を探すよりも簡単です)。 次のようなものが得られます。

関数としての画像
メソッドをさらに説明するために、いくつかの表記法を紹介する必要があります。
まず、画像をピクセル座標の関数として考えます。 したがって、
座標と
座標を持つピクセルが白であると言いたい場合は、
I(x,y)==255書くことができます。
さらに、関数がある場合は、その関数から派生関数を取得することができ、それが便利になります。 離散関数、つまり、指定されたステップの間にセルで定義されている関数があるため、次のように記述できます(関数は2次元であるため、それぞれ2つの導関数があります)。
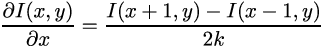
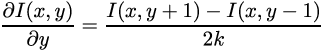
ここでは、隣接するピクセル間の差= 1ピクセルなので、
k==1です。
したがって、導関数も元の画像と同じサイズの行列になります。


両方の座標に関して導関数があるので、勾配を計算することは論理的です:
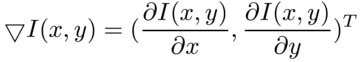
そしてその価値:
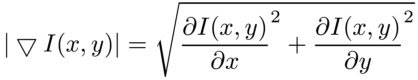
勾配の大きさは画像として表示できます:

次に、勾配の大きさを詳しく見てみましょう。 必要な情報が保存されている場所は非常に重要です。
画像のノイズを取り除くには、ぼかしをかける必要があります。 ただし、ぼかしは重要な詳細を失います。 つまり、グラデーションが十分に大きい領域のぼかしを制限したいと思います。 残ったのは、これを行う方法の問題だけでした。
拡散プロセスとの接続
ここで、拡散の素晴らしい物理的プロセスが私たちの助けになります。 平面内の特定の点での質量の存在の指標として画像行列を想像してください。 拡散プロセスは、質量が大きな濃度のポイントから小さな濃度のポイントに「広がる」という事実に基づいています。 拡散のプロセスには、いわゆるフィックの法則に従う流れの概念があります。

ここで、
Dは拡散の方向と大きさを定義する拡散テンソルです。
また、質量保存の法則を書きます。これは、流入と流出の流れの差がその時点での質量の変化に等しいことを示しています。
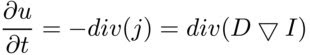
流れが制限されていない場合、つまり
D==1質量はすべての方向に均一に広がります。つまり、ガウスぼかしと同等になります。つまり、重要な画像の詳細が失われます。 フローを制限できる方法に興味があります。
最も単純な方法の1つは、方向を制限せずにフローの大きさを制限することです。 彼についてさらに説明します。
勾配の大きさを入力するために、いくつかの減少関数を紹介しましょう。 この段階でのこの関数は、拡散テンソルになります。

次に、質量保存方程式は次の形式を取ります。

次に、すべての式を書き(おそらくこの手順は省略します)、問題の解決策を見つけるための最終的な式を書きます。
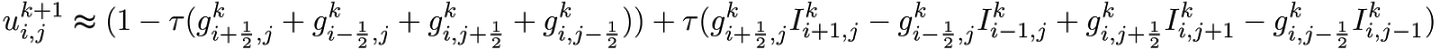
したがって、パラメーター値
tau<=0.25安定した反復スキームが得られました。 基本的な方法とより成功したアルゴリズムがそれに基づいているため、かなり遅いです。
結果
最終的に、ほとんどすべての重要な詳細を保持し、ほとんどすべてのノイズを失った画像が得られます。
UPD:心から謝罪します。画像が混同されました。 画像を置き換えました。これは、記事に記載されているのと同じくらい多くのノイズで画像を処理した結果として得られたものに関して以前のものでした。 改めておaび申し上げます。

比較のために-元のバージョンとノイズのあるバージョン(もう一度):


参照:
- P. Perona、J。Malik:異方性拡散を使用したスケール空間およびエッジ検出。 IEEE
パターン分析と機械知能に関するトランザクション12(7):629-639、1990。 - J.ヴァイケルト:画像処理における異方性拡散。 Teubner、シュトゥットガルト、1998年。本は
もう利用できませんが、ヨアヒム・ワイッカートの博士論文は、彼の基礎でした
本、彼のウェブサイトで入手可能です。 - T. Brox:コンピュータービジョンに関する講義。 フライブルク・イム・ブライスガウ、2011
PS不正確な点を見つけたら-批判や提案を聞いてうれしいです。