読者の皆さん、私はあなたのことは知りませんが、バイナリ検索ツリーの概念に具現化された基本的な考え方の恵みと、
バランスの取れたバイナリ検索ツリー(
赤黒木 、
AVL木 、
デカルト木 )の実装の複雑さとの対比にいつも驚いていました。 最近、Sedgwick [
1 ]を再度めくると、ランダム化された検索ツリーの説明が見つかりました(元の作品[
2 ]も見つかりました)-ページの3分の1(ノードの挿入、別のページ-削除ノード)を占めるほど単純です。 さらに、詳しく調べると、検索ツリーからノードを削除する操作の非常に美しい実装という形で、追加のボーナスが発見されました。 次に、C ++実装であるランダム化された検索ツリーの説明(カラー写真付き)、および説明されたツリーのバランスに関する小規模なオーサリング研究の結果を見つけます。
少しずつ始めましょう
ツリーの完全な実装について説明するので、最初から始めなければなりません(専門家はいくつかのセクションを安全にスキップできます)。 バイナリ検索ツリーの各ノードには、基本的にすべてのプロセスを制御するキーキー(全体が含まれます)、および左右のサブツリーへの左右のポインターのペアが含まれます。 ポインターがヌルの場合、対応するツリーは空です(つまり、単に存在しません)。 さらに、ランダム化されたツリーを実装するために、このノードにルートを持つツリーのサイズを(頂点の
オウムで )保存する別のサイズフィールドが必要になります。 ノードは構造によって表されます:
struct node // { int key; int size; node* left; node* right; node(int k) { key = k; left = right = 0; size = 1; } };
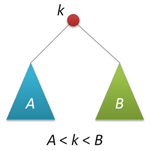
検索ツリーの主な特性は、左のサブツリーのキーはルートキーよりも小さく、右のサブツリーではルートキーよりも大きいことです(明確にするために、すべてのキーが異なると仮定します)。 このプロパティ(右の図に概略を示す)を使用すると、ルートキーの値に応じて、ルートから右または左に移動して、特定のキーの検索を非常に簡単に整理できます。 検索関数の再帰バージョン(およびこれだけを検討します)は次のとおりです。
node* find(node* p, int k) // k p { if( !p ) return 0; // if( k == p->key ) return p; if( k < p->key ) return find(p->left,k); else return find(p->right,k); }
ツリーに新しいキーを挿入します。 クラシックバージョンでは、空のポインターに合わせて休憩するときに新しいノードを作成し、行き止まりが見つかった場所まで一時停止するという違いがありますが、挿入は検索を繰り返します。 最初は、この関数をペイントしたくありませんでした。ランダム化された場合、少し異なる動作をするからです。 いくつかの点を修正したい。
node* insert(node* p, int k) // k p { if( !p ) return new node(k); if( p->key>k ) p->left = insert(p->left,k); else p->right = insert(p->right,k); fixsize(p); return p; }
まず、指定されたツリーを変更する関数は、新しいルートへのポインターを返し(変更されたかどうかは関係ありません)、呼び出し元の関数はこのツリーをどこに掛けるかを決定します。 第二に、なぜなら ツリーのサイズを保存する必要がある場合、サブツリーの変更については、ツリー自体のサイズを調整する必要があります。 次のいくつかの関数がこれを行います。
int getsize(node* p) // size, (t=NULL) { if( !p ) return 0; return p->size; } void fixsize(node* p) // { p->size = getsize(p->left)+getsize(p->right)+1; }

挿入機能の何が問題になっていますか? 問題は、この関数は結果のツリーのバランスを保証しないことです。たとえば、キーが昇順で供給される場合、ツリーはすべての付随する「グッディーズ」を持つ一重リンクリスト(図を参照)に縮退します。
そのようなツリーでの
すべての操作(バランスのとれたツリーでは、今回は対数です)。 不均衡を回避するにはさまざまな方法があります。 従来は、バランスを保証するクラス(赤黒木、AVLツリー)と確率的な意味で提供するクラス(デカルトツリー)の2つのクラスに分けることができます。不均衡なツリーを取得する確率は、大きなツリーサイズでは無視できます。 ランダム化されたツリーが2番目のクラスに属すると言っても、驚くことではないでしょう。
ツリーのルートに挿入する
ランダム化に必要なコンポーネントは、新しいキーの特別な挿入の使用です。その結果、新しいキーはツリーのルートにあります(最近挿入されたキーへのアクセスは非常に高速で、
自己組織化リストに感謝します )。 ルートへの挿入を実装するには、ローカルツリー変換を実行する回転関数が必要です。
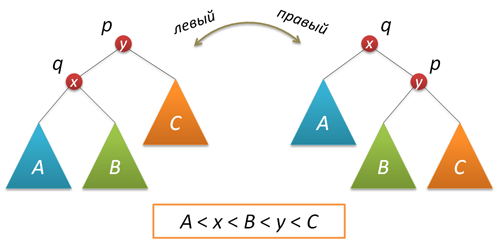
サブツリーのサイズを調整し、新しいツリーのルートを返すことを忘れないでください。
node* rotateright(node* p) // p { node* q = p->left; if( !q ) return p; p->left = q->right; q->right = p; q->size = p->size; fixsize(p); return q; }
node* rotateleft(node* q) // q { node* p = q->right; if( !p ) return q; q->right = p->left; p->left = q; p->size = q->size; fixsize(q); return p; }
これで実際のルートへの挿入。 最初に、左または右のサブツリーのルートに新しいキーを再帰的に挿入し(ルートキーとの比較の結果に応じて)、ツリーのルートに必要なノードを上げる右(左)回転を実行します。
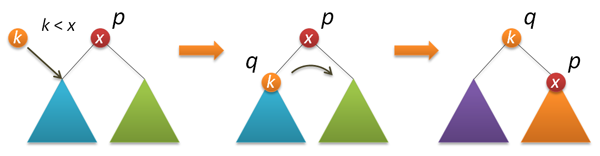
node* insertroot(node* p, int k) // k p { if( !p ) return new node(k); if( k<p->key ) { p->left = insertroot(p->left,k); return rotateright(p); } else { p->right = insertroot(p->right,k); return rotateleft(p); } }
ランダム化された挿入
そこで、ランダム化を行いました。 現時点では、simpleとrootの2つの挿入関数があります。これらの関数は現在、ランダム化された挿入を組み合わせています。 このすべての意味は、次のアイデアです。 すべてのキーを事前に混合し、それらからツリーを構築すると(ミキシング後に取得した順序で標準スキームに従ってキーが挿入される)、構築されたツリーはバランスがとれていることが知られています(その高さは、log
2 nに対してlog
2 nのオーダーであり、完全にバランスが取れています)ツリー)。 この場合、ルートはソースキーのいずれかと同じ確率であることに注意してください。 どのキーを使用するか事前にわからない場合(たとえば、ツリーを使用するプロセスでシステムに入力されます)。 実際、すべてがシンプルです。 任意のキー(ツリーに挿入する必要があるキーを含む)が確率1 /(n + 1)(nは挿入前のツリーのサイズ)のルートになることがあるため、指定された確率でルートへの挿入を実行します。確率1-1 /(n + 1)-ルートのキー値に応じて、右または左のサブツリーに再帰的に挿入します。
node* insert(node* p, int k) // k p { if( !p ) return new node(k); if( rand()%(p->size+1)==0 ) return insertroot(p,k); if( p->key>k ) p->left = insert(p->left,k); else p->right = insert(p->right,k); fixsize(p); return p; }
それがトリックです...それがどのように機能するかを確認しましょう。 500ノードのツリーを作成する例(0から499までのキーが昇順で受信されました):
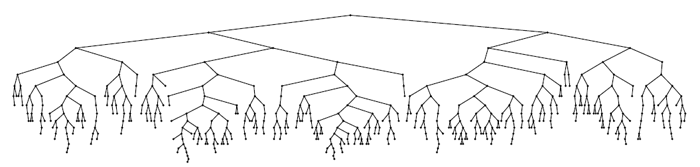
美の理想とは言いませんが、身長は明らかに小さいです。 タスクを複雑にします-0〜2
14 -1(理想的な高さは14)のキーを指定してツリーを構築し、構築プロセス中に高さを測定します。 信頼性を高めるために、1,000回実行して結果を平均します。 結果がマーカーでマークされている次のグラフを取得します。実線は[
3 ]-h = 4.3ln(n)-1.9ln(ln(n))-4からの理論的推定です。 図からわかる最も重要なことは、確率論は力だということです!
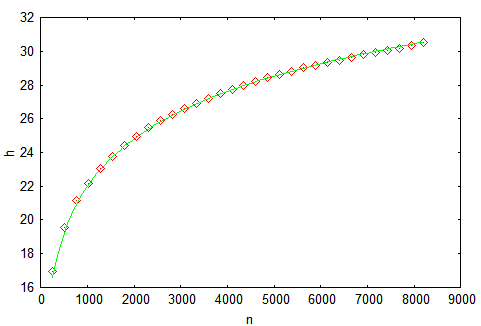
提案されたグラフは、多数の計算に対してツリーの高さの
平均値を示していることを理解する必要があります。 そして、1つの特定の計算で高さがどれだけ異なるか。 上記の記事には、この質問に対する答えがあります。 4095ノードを挿入した後、小作人の作業を行い、高さの分布のヒストグラムを作成します。
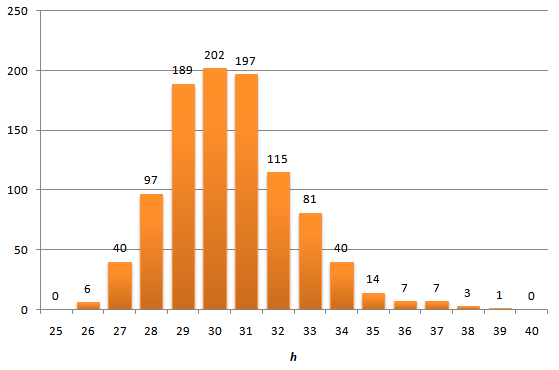
一般に、犯罪は見られず、分布の尾は短く、得られた最大の高さは39であり、
病院の平均を大幅に超えていません。
キーの削除
したがって、バランスの取れた(少なくともある意味では)ツリーがあります。 確かに、ノードの削除はサポートしていません。 これが私たちが今やることです。 多くの教科書で規定されており、
ハブ上で(写真で)よく説明されている削除オプションは、すぐに機能しますが、非常に見栄えがよくありません(挿入と比較して)。 この素晴らしい
投稿で示されたように、私たちは逆の方向に進みます(私の意見では、これはデカルトの最高の記述です)。 ノードを削除する前に、ツリーを接続する方法を学びます。 根がpとqの2つの探索木が与えられ、最初のツリーのキーが2番目のツリーのキーよりも小さいとします。 これら2つのツリーを1つに結合する必要があります。 新しいツリーのルートとして、2つのルートのいずれかを取ることができます。それをpとします。 次に、pの左サブツリーをそのまま残し、pの右サブツリーとツリー全体qの2つのツリーの結合をpの右側で中断できます(問題のすべての条件を満たす)。

一方、同じ成功で、ノードqを新しいツリーのルートにすることができます。 ランダム化された実装では、これらの選択肢の選択はランダムに行われます。 左のツリーのサイズをn、右のツリーのサイズをmとします。 次に、確率n /(n + m)の新しいルートでpが選択され、確率m /(n + m)のqが選択されます。
node* join(node* p, node* q) // { if( !p ) return q; if( !q ) return p; if( rand()%(p->size+q->size) < p->size ) { p->right = join(p->right,q); fixsize(p); return p; } else { q->left = join(p,q->left); fixsize(q); return q; } }
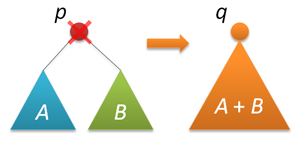
これですべてを削除する準備ができました。 キーで削除します-指定されたキーを持つノードを探し(すべてのキーが異なることを思い出します)、このノードをツリーから削除します。 検索段階は検索中と同じですが(奇妙なことに)、この方法で行います-見つかったノードの左右のサブツリーを結合し、ノードを削除して、マージされたツリーのルートを返します。
node* remove(node* p, int k) // p k { if( !p ) return p; if( p->key==k ) { node* q = join(p->left,p->right); delete p; return q; } else if( k<p->key ) p->left = remove(p->left,k); else p->right = remove(p->right,k); return p; }
削除してもツリーのバランスが崩れないことを確認してください。 これを行うには、2
15個のキーでツリーを構築し、半分(0〜2
14 -1の値)を削除して、高さの分布を確認します...

「証明」するために必要な実質的に違いはありません...
結論の代わりに
ランダム化された二分探索木の間違いない利点は、その実装の単純さと美しさです。 ただし、ご存知のように、無料のケーキは存在しません。 この場合、何を支払うのですか? まず、サブツリーサイズを格納するための追加メモリ。 ノードごとに1つの整数フィールド。 赤黒木では、ある程度のスキルがあれば、追加フィールドなしで行うことができます。 一方、ツリーのサイズは完全に無駄な情報ではありません。これにより、データへのアクセスを番号で整理できるようになり(選択タスクまたは順序統計の検索)、実際にはツリーを要素を挿入および削除できる順序付き配列に変換します。 第二に、対数時間が機能していますが、比例定数はかなり大きいと思われます-ほとんどすべての操作は2回のパス(上下両方)で実行され、さらに、挿入と削除には乱数が必要です。 良いニュースがあります-すべてが検索段階で非常に迅速に機能するはずです。 最後に、深刻なアプリケーションでこのようなツリーを使用する場合の基本的な障害は、対数時間が保証されないことです。ツリーのバランスが不十分になる可能性が常にあります。 確かに、数万のノードが存在する場合でも、このようなイベントの確率は非常に小さいため、おそらくチャンスを得ることができます...
ご清聴ありがとうございました!
文学
- ロバート・セジウィック、C ++アルゴリズム、M .:ウィリアムズ、2011- ちょうど良い本
- マルティネス、コンラード; Roura、Salvador(1998)、 Randomized binary search trees 、Journal of the ACM(ACM Press)45(2):288–323- オリジナル記事
- リード、ブルース(2003)、 ランダムバイナリサーチツリーの高さ 、Journal of the ACM 50(3):306–332- ツリーの高さの推定