計算幾何学、またはどのようにしてオリンピアードプログラミングに関与したかパート1

こんにちは、愛するhabravchane！ これは私の2番目の記事であり、計算幾何学についてお話したいと思います。

ちょっとした歴史

私はすでに数学学部の4年生です。プログラミングを始める前は、自分は100％数学者だと思っていました。

最初の年の終わりに、olympiadプログラミングに携わっているコンピューターサイエンスの先生が私に注目を集めました。 チームごとに1人の数学者が不足していました。 だから、彼らは私にオリンピアードのプログラミングに慣れ始めました。 率直に言って、私にとっては非常に困難でした。最初の年にDelphiという言葉を学んだ人にとって。 しかし、私の先生は非常に有能な専門家であることが判明し、私に良いアプローチを見つけました。 彼は私に数学的な問題を与え始めました。私は最初に純粋に数学的に解決し、それからコードを書きました（半分の罪で）。

私は先生のアプローチが本当に好きです。「このトピックに対処してから、教えてください。そうすれば、みんなが理解できるように」

したがって、私が担当する最初の本当に重要なタスクは、正確な計算幾何学であり、コンピューターサイエンスのこのセクションの典型的なタスクを理解する必要がありました。 そして、私はすべての責任を持ってこのタスクに取り組むことにしました。

informatics.mccme Webサイトのすべてのテストに合格するように、これらのタスクでどれだけ苦労したかを覚えています。 しかし今、私はすべてのテストを通過したことを非常に嬉しく思い、計算幾何学の問題が何であるかを知っています。

エントリー

「計算幾何学は、幾何学問題を解決するためのアルゴリズムを研究するコンピューターサイエンスの一分野です。 このような問題は、コンピューターグラフィックス、集積回路の設計、技術的なデバイスなどで発生します。このような問題の初期データは、多くのポイント、セグメントのセット、ポリゴンなどです。 結果は、何らかの質問に対する答え、または何らかの幾何学的なオブジェクトのいずれかです。」

この記事は十分に大きいので、2つの部分に分割することにしました。最初の部分はポリゴン、2番目の部分はさまざまな幾何学的オブジェクトの相対位置に当てられます。

ベクトルに関する少しの理論

どの端が開始と見なされ、どの端が終了であるかが示されているセグメントは、ベクトルと呼ばれます。 空間内の任意の点もベクトルと見なすことができます。 このようなベクトルはゼロと呼ばれます。 ゼロベクトルの開始と終了は一致し、特定の方向はありません。


非ゼロベクトルABの長さは、セグメントABの長さです。 ゼロベクトルの長さはゼロに等しいと見なされます。
2つの非ゼロベクトルは、同一線上または平行線上にある場合、共線性と呼ばれます。 2つの非ゼロベクトルABとCDが同一直線上にあり、光線ABとCDが同方向の場合、ベクトルABとCDは同方向と呼ばれ、これらの光線が同方向でない場合、ベクトルABとCDは反対方向と呼ばれます。 ゼロベクトルは、任意のベクトルと整列していると見なされます。

ベクトルのスカラー積

ベクトルのスカラー積は、これらのベクトルの長さとベクトル間の角度の余弦の積に等しい数です。
（a、b）= | a || b |cos∠（a、b）

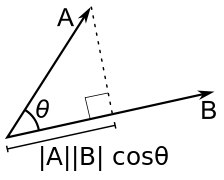
ベクトルが座標a（x ₁ 、y ₁ ）、b（x ₂ 、y ₂ ）で与えられる場合、スカラー積（a、b）= x ₁ x ₂ + y ₁ y ₂ 。

ベクトルの斜積

平面内のベクトルの擬似スカラーまたは斜めの積は数と呼ばれます
[a、b] = | a || b |sinθ
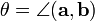
どこで -aからbまでの回転角度（反時計回り） ベクトルaとbの少なくとも1つがゼロの場合、[a、b] = 0を置きます。
ベクトルの座標がa（x ₁ 、y ₁ ）、b（x ₂ 、y ₂ ）の場合、スキュー積[a、b] = x ₁ y ₂ -x ₂ y ₁ 。
ベクトルの幾何学的に斜めの積は、これらのベクトルがまたがる平行四辺形の方向付けられた領域です。


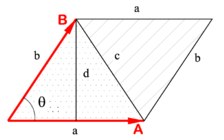
計算幾何学の問題におけるベクトルのスキュー積は、組み合わせ論の再帰と同じ場所にあります。 これは一種の計算幾何学の真珠です。 計算幾何学のほとんどすべての問題には、正面の解決策の代わりにスキュー積を使用した簡単な解決策があります。

練習しましょう

三角形から始めましょう

タスク番号1

タスクは非常に単純です。つまり、入力された3つの数字a、b、cを使用して、そのような辺を持つ三角形が存在するかどうかを判断します。

解決策
ここで、三角形の不等式のみをチェックする必要があることは明らかです。a+ b> c、a + c> b、b + c> a。 興味深いことに、三角形の不等式を研究するとき、私だけに質問がありました：負の数もこれらの3つの不等式を満たせますか？ いいえ判明！ 各不等式を合計すると、a> 0、b> 0、c> 0になります。したがって、三角形の不等式は、三角形が存在するための必要十分条件です。

タスク番号2

タスクは前のタスクと非常に似ていますが、三角形は辺ではなく、頂点の座標によって定義されるという違いがあります。

解決策
一見したところ、解決策は明白に思えます。三角形の辺を計算し、問題を前の辺に減らします。 ただし、2点A（x ₁ 、y ₁ ）、B（x ₂ 、y ₂ ）の間の距離は、式√（x ₁ -x ₂ ） ² +（y ₁ -y ₂ ） ²によって計算されるため、ルートの損失が発生する可能性がありますこれは、三角形の不等式をチェックするのに悪いです。 三角形がその頂点の座標によって定義されている場合、その辺の長さを計算して三角形の不等式をチェックする必要はないことがわかります。 この場合、これらの3つの点が1つの直線上にある場合にのみ、三角形は存在しません。 そして、これはベクトルの斜めの積によって簡単に検証されます。 ゼロに等しい場合、ベクトルは同一直線上にあります。つまり、3つのポイントはすべて1つの直線上にあります。


次のすべての問題では、三角形の存在をチェックする手順を調べただけなので、三角形が存在すると仮定します。

タスク番号3

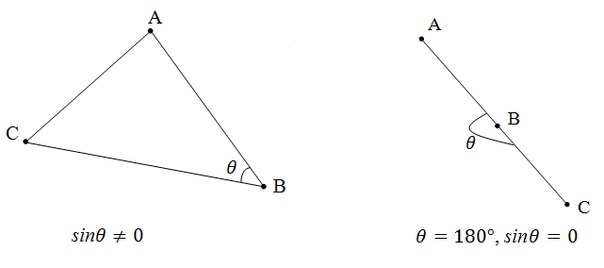
三角形は辺で設定されます。 三角形のタイプを決定します：鈍角、長方形または鋭角。

解決策
三角形の各種類を思い出してください。



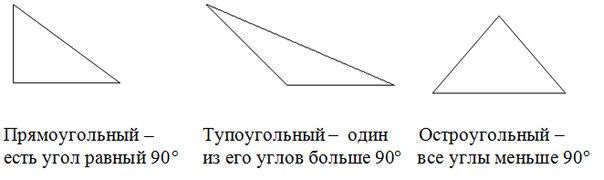
幾何学のコースから、反対側ではより大きな角度があることがわかっています（必要です）。 したがって、大きな角度が何であるかを知ると、三角形のタイプを理解できます。

1. 90°より大きい角度-鈍角三角形
2. 90°未満の角度-鋭角三角形
3. 角度は90°-三角形は長方形

コサイン定理を使用します。


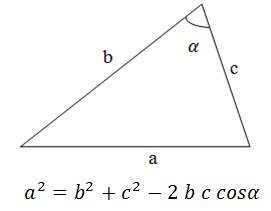
明らかに、角度の余弦がゼロより大きい場合、角度は90°未満、ゼロの場合、角度は90°、ゼロ未満の場合、角度は90°を超えます。 ただし、少し考えてみると、角度の余弦を計算する必要はなく、その符号のみを考慮する必要があることを理解できます。

• cosα> 0の場合、a ² <b ² + c ²は鋭角三角形
• cosα= 0の場合、a ² = b ² + c ²は直角三角形です
• cosα<0の場合、a ² > b ² + c ²は鈍角三角形

aは大きな側面です。

タスク番号4

タスクは前のタスクに似ていますが、三角形のみがその辺ではなく、頂点の座標によって設定されます。

解決策
問題2と同様に、このタスクは前のタスクに完全に削減されていると言えます（そのまま）。 ただし、2番目の問題と同様に、解決策は単純化できます。 一般に、三角形がその頂点の座標によって定義されている場合、辺を計算するよりもベクトルを使用して作業する方が常に簡単です。 前のタスクと同様に、三角形のどの角度が最も大きいかを判断する必要があります。 角度のタイプは、それを形成するベクトルのスカラー積の符号によって簡単に決定されます。鋭角の場合は正、直角の場合はゼロ、鈍角の場合は負です。 したがって、3つすべてのスカラー積をカウントして乗算する必要があり、この数の符号で三角形のタイプを判断できます。

タスク番号5

指定された辺で三角形の面積を見つけます。

解決策
明らかな解決策は、ヘロンの式を適用することです。

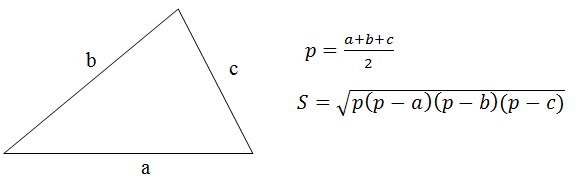
ところで、誰もこの式の証明に興味がありませんでしたか？

タスク番号6

頂点の座標によって与えられる三角形の面積を計算します。

解決策
前の問題に還元される解決策については説明しませんが、編組製品の幾何学的な意味を使用するようにします。 2つのベクトルの幾何学的に斜めの積は、これらのベクトル上に引き伸ばされた平行四辺形の方向付けられた領域を定義します。 平行四辺形の対角線は2つの等しい三角形に分割するため、三角形の面積は平行四辺形の面積の半分であることがわかります。
ベクトルa（x ₁ 、y ₁ ）、b（x ₂ 、y ₂ ）

S =（x ₁ y ₂ -x ₂ y ₁ ）/ 2-三角形の向きの領域

タスク番号7

頂点の座標で与えられる点と三角形が与えられます。 ポイントがこの三角形の内側、境界線、または外側にあるかどうかを判断します。

解決策
このタスクには、根本的に異なる2つのソリューションがあります。 最も魅力的なものから始めましょう。

エリア法

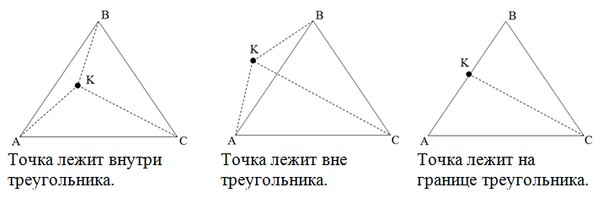
三角形AKB、AKC、BKCの面積の合計（方向付けられていないが「通常」）が三角形ABCの​​面積より大きい場合、ポイントは三角形の外側にあります。 最初の3つのエリアの合計が4番目のエリアに等しい場合、3つのエリアの1つがゼロに等しいかどうかを確認する必要があります。 等しい場合、ポイントは三角形の境界上にあり、そうでない場合は内側にあります。
当然、ベクトルの斜積によって三角形の面積を計算する必要があります。 この方法はあまり良くありません。 ここでは浮動小数点比較が使用されるため、比較時に誤った決定が行われる可能性があります。 再び、2番目の方法はベクトルに基づいており、あらゆる点ではるかに効果的です。

ハーフプレーンチェック

三角形の辺の少なくとも1つが、その反対側の頂点と異なる半平面に沿ったポイントを「広げ」ている場合、ポイントは三角形の外側にあります。 それ以外の場合、ポイントが三角形の辺を含む少なくとも1つの線に属する場合、三角形の境界上にあります。 それ以外の場合、ポイントは三角形の内側にあります。

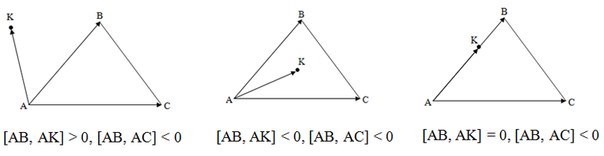
最初の例では、辺ABは頂点Cと点Kを異なる半平面に分割するため、点は外側にあります。

タスク番号8

頂点の座標によって与えられるポリゴンの面積の計算。

解決策
ポリゴンとは、単純なポリゴン、つまり自己交差のないポリゴンを意味します。 さらに、凸型または非凸型のどちらでもかまいません。

この問題は2つの方法で解決できます。台形と三角形の方向付けられた面積を計算することです。

台形法

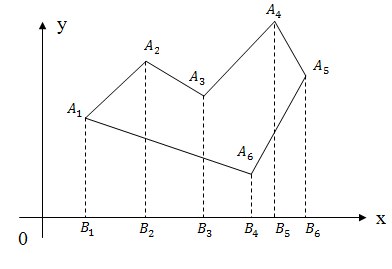
多角形の面積を計算するには、図に示すように台形に分割し、結果の台形の方向付けられた領域を追加する必要があります。これが元の多角形の方向付けられた領域になります。
S = S _{A 1 A 2 B 2 B 1} + S _{A 2 A 3 B 3 B 2} + S _{A 3 A 4 B 5 B 3} + S _{A 4 A 5 B 6 B 5} + S _{A 5 A 6 B 4 B 6} + S _{A 6 A 1 B 1 B 4}
よく知られている公式に従って、台形の面積を考慮します：高さに対する塩基の合計の半分
S _{A 1 A 2 B 2 B 1} = 0.5 *（A ₁ B ₁ + A ₂ B ₂ ）*（B ₂ -B ₁ ）

結果の領域は方向付けられているため、そのモジュラスを計算する必要があります。

三角形の方法

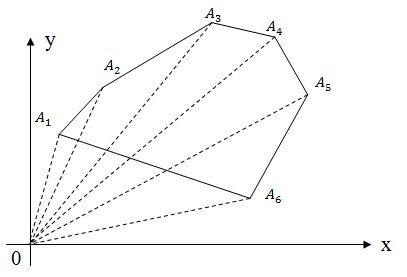
前の方法と同様に、図に示すように、多角形を台形ではなく三角形に分割することができます。 その結果、これらの三角形の方向付けられた領域を合計すると、再び多角形の方向付けられた領域が得られます。
S = S _{O A 1 A 2} + S _{O A 2 A 3} + S _{O A 3 A 4} + S _{O A 4 A 5} + S _{O A 5 A 6} + S _{O A 6 A 1}

ご覧のとおり、ポリゴンの面積を計算するタスクは非常に簡単です。 理由はわかりませんが、台形で割ることによってこの問題を解決することを好みます（おそらくすべてのオリンピックでこのように解決したためです）。 さらに、2番目のソリューションでは、三角形の面積を斜めの積で計算する必要があります。 ヘロンの式を忘れてはいけない!!!

タスク番号9

多角形は、頂点の座標によって、トラバーサルの順序で与えられます。 ポリゴンが凸面かどうかを確認する必要があります。

解決策
多角形は、その辺を含む線に対して1つの半平面にある場合、凸と呼ばれます。


問題は、ベクトルのスキュー積の計算に戻ります。つまり、凸多角形の場合、スキュー積[A _i A _{i + 1} 、A _{i + 1} A _{i + 2} ]の符号は正または負です。 したがって、ラウンドの方向がわかっている場合、凸多角形のスキュー積の符号は同じです。反時計回りに回る場合は負ではなく、時計回りに回る場合は正ではありません。

タスク番号10

平面上の多角形（必ずしも凸面ではない）は、その頂点の座標によって与えられます。 整数座標が内部にある（ただし境界上にない）ポイントの数をカウントする必要があります。

解決策
この問題を解決するために、補助的な問題を考えます。セグメントは整数であるその端の座標によって与えられます。 セグメント上にある整数ポイントの数を計算する必要があります。 セグメントが垂直または水平の場合、端の座標を減算して追加する必要があることは明らかです。 興味深いのは、セグメントが垂直でも水平でもない場合です。 この場合、セグメントを直角三角形に完成させる必要があり、答えは、この三角形の足の長さの最大公約数に1を足した数になります。


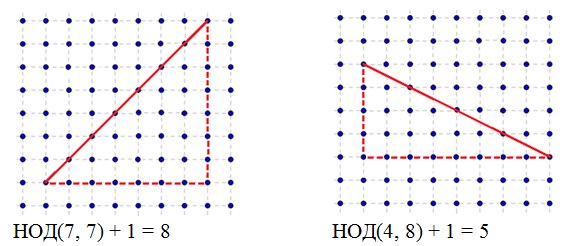
頂点の整数座標を持つ多角形の場合、ピーク式は有効です：S = n + m / 2-1、ここでSは多角形の面積、nは厳密に多角形の内側にある整数点の数、mは多角形の境界にある整数点の数です。 多角形の面積の計算方法はわかっているので、Sは既知です。 また、ポリゴンの境界にある整数ポイントの数を計算することもできます。そのため、Peak式には、未知の不明な未知数が1つしかありません。
例を考えてみましょう：

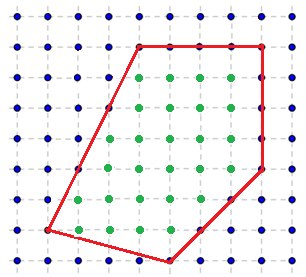
S = 16 + 4 + 4.5 + 6 + 1 + 2 = 33.5
m = 15
n = 33.5-7.5 +1 = 27-ポイントは厳密にポリゴンの内側にあります
この問題は解決されました！

以上です！ この記事を楽しんでいただけたことを願っています。第2部を書きます。