ABBYYでの
就職についての記事を読んでいるときに、その問題について言及しました。
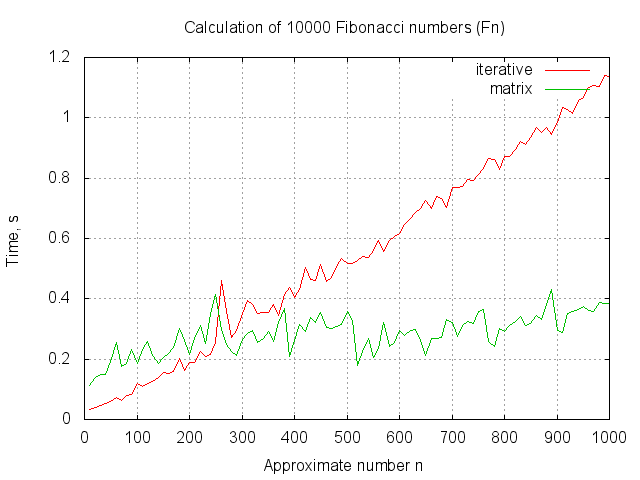
すばやく-数値のO(log N)算術演算の場合-N番目のフィボナッチ数を見つける
私はそれについて考え、O(N)の間に機能するソリューションのみが頭に浮かぶことに気付きました。 しかし、解決策は後で見つかりました。
便宜上、表記から移動します

に
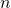
。 セットにも表記法を使用します。

非負の整数

正の整数です。 事実、さまざまな数学的伝統では、多くの自然数に0が含まれる場合と含まれない場合があります。したがって、国際数学のテキストでは、これを明示的に示すことが推奨されています。
だから解決策
ナッツ[
1、p。 112 ]は、次の形式の行列IDを提供します。

身元は証明なしで与えられますが、帰納法によって非常に簡単に証明されます。
右側のマトリックスは、Qマトリックスと呼ばれることもあります。
注:
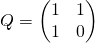
アイデンティティからそれを得る

。 つまり 計算する
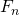
行列を計算する必要があります
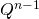
そして、最初の行の最初の要素(1から番号付け)を取得します。
計算以来
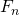
行列を累乗することに還元された場合、このプロセスをより詳細に検討します。
マトリックスを用意しましょう
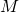
力に引き上げられる
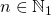
。 また、
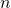
2のべき乗、つまり
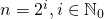
。
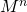
ツリーとして表すことができます:
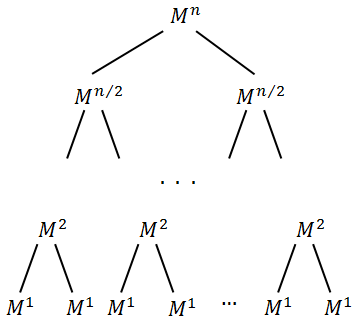
これは以下を参照します:
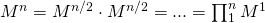
。
したがって、行列を計算するには
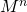
行列を計算する必要があります

そしてそれ自体で乗算します。 計算する

あなたは同じことをする必要があります
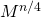
など
明らかに、木の高さは
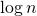
。
計算時間を見積もる
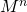
。 マトリックス
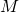
ある程度までは一定のサイズを持ちます。 したがって、2つの行列の任意の程度への乗算は、
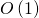
。 そのような乗算はすべて実行する必要があります

。 したがって、計算の複雑さ
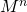
等しい
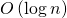
。
また、nが2のべき乗でない場合はどうなりますか?
ここで疑問が生じます:もしも
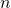
2のべき乗ではありませんか? 任意の自然数
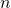
は、2のべき乗である数の合計として分解できます。繰り返しは行われません(2進数から10進数に変換するたびにこれを行います)。 つまり

、
どこで

-コンクリートが何度も通過する
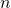
。 思い出すと
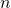
行列の次数である場合、次のようになります。
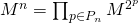
。
一般に、行列積は可換ではありませんが、 乗算中のオペランドの順序は重要ですが、いわゆる 順列行列の可換性が尊重されます。 マトリックス
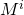
はの順列です
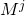
、

。 したがって、乗算するときにオペランドの順序を覚えておく必要はありません。
したがって、計算アルゴリズム
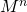
以下のステップとして表すことができます。
- 分解する
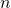 セットの形式での2の累乗の合計
セットの形式での2の累乗の合計 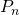 。
。 - セットのすべての要素を計算する
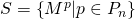 。
。 - 計算する
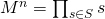 。
。
このアルゴリズムの実行時間を推定します。
最初のステップは時間内に完了します
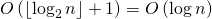
どこで
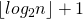
-ビット数
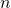
。
2番目のステップは
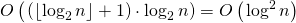
なぜなら もう完了する必要はありません
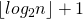
行列を累乗します。
3番目のステップは
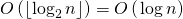
なぜなら もう行列の乗算を実行する必要はありません

回。
最適化
このアルゴリズムの実行時間を改善することは可能ですか? はい、できます。 2番目のステップでは、セット内の行列を計算する方法

。 私たちはそれらについてそれぞれ知っている

2のべき乗です。 ツリーのある図に戻ると、これらはすべてツリーの特定の階層にあり、大きな階層を計算するには、小さな階層を計算する必要があります。
メモ化手法を適用し、計算された行列をツリーのすべての層に保存すると、2番目のステップの作業時間を短縮できます。
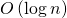
アルゴリズム全体の実行時間もアップしています
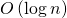
。 これは、問題の状態によって必要なものです。
コード
コーディングに移りましょう。 次の2つの理由から、Pythonでアルゴリズムを実装しました。
- 擬似コードを置き換えるのに十分な表現力があります。
- 透過的な長演算があります。
これは次のとおりです。
class MatrixFibonacci:
Q = [[1, 1],
[1, 0]]
def __init__(self):
self.__memo = {}
def __multiply_matrices(self, M1, M2):
"""
( 2x2)."""
a11 = M1[0][0]*M2[0][0] + M1[0][1]*M2[1][0]
a12 = M1[0][0]*M2[0][1] + M1[0][1]*M2[1][1]
a21 = M1[1][0]*M2[0][0] + M1[1][1]*M2[1][0]
a22 = M1[1][0]*M2[0][1] + M1[1][1]*M2[1][1]
r = [[a11, a12], [a21, a22]]
return r
def __get_matrix_power(self, M, p):
""" ( p )."""
if p == 1:
return M
if p in self.__memo:
return self.__memo[p]
K = self.__get_matrix_power(M, int(p/2))
R = self.__multiply_matrices(K, K)
self.__memo[p] = R
return R
def get_number(self, n):
""" n-
( n )."""
if n == 0:
return 0
if n == 1:
return 1
powers = [int(pow(2, b))
for (b, d) in enumerate(reversed(bin(n-1)[2:])) if d == '1']
matrices = [self.__get_matrix_power(MatrixFibonacci.Q, p)
for p in powers]
while len(matrices) > 1:
M1 = matrices.pop()
M2 = matrices.pop()
R = self.__multiply_matrices(M1, M2)
matrices.append(R)
return matrices[0][0][0]
mfib = MatrixFibonacci()
for n in range(0, 128):
num = mfib.get_number(n)
print(num)
,

. :
def get_number(self, n):
if n == 0:
return 0
a = 0
b = 1
c = 1
for i in range(n-1):
c = a + b
a = b
b = c
return c
.

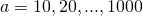
.

MatrixFibonacci IterationFibonacci (, ). 10 000

.
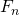
. :
n <tab> T1 <tab> T2. .
, -
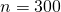
(c ,

64 ). , , .
. gnuplot —
.
P.S. , TeX- . , .
- . , 1. . — 3- . — .: «», 2006.