別のフィボナッチ数計算アルゴリズム

記事を読む前に、O（log N）の漸近的な振る舞いを持つ独自のアルゴリズムを考え出すことにしました。 それほど時間はかかりませんでした。 以下に、アイデアの説明とC ++の例を示します。

この式を取得するだけです：
どこで

式は帰納法によって簡単に証明されます。 m = 0の場合、式は真です。

式がm = pに対して真であると仮定します

式がm = p + 1に対して有効であることを証明しましょう。

-m = pの場合と同じ式を受け取った、つまり m = p + 1の場合、式は真のままです
入手が簡単 同じ番号で：

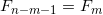
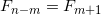
N、mが奇数の場合、等式が そして 。 この数は
単純化した後、次の式を取得します。




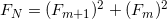
最新の式を使用すると、単純な再帰アルゴリズムを取得できます。

#include <iostream> using namespace std; void fibonachi_recursive(int n, int& fn, int& fn1) { int gn, gn1; if (n < 2) { fn = n; fn1 = 1; return; } fibonachi_recursive(n / 2, gn, gn1); if (n % 2) { fn = gn1 * gn1 + gn * gn; fn1 = gn1 * gn1 + 2 * gn * gn1; } else { fn = 2 * gn * gn1 - gn * gn; fn1 = gn1 * gn1 + gn * gn; } } int fibonachi(int n) { int fn, fn1; fibonachi_recursive(n, fn, fn1); return fn; } int main() { for (int i = 0; i < 20; i++) cout << fibonachi(i) << " "; return 0; } 

再帰から逃れるのは簡単です：

 #include <iostream> using namespace std; unsigned fibonachi(unsigned n) { if (n < 2) return n; unsigned mask = 1, m = n; while (m > 1) { m >>= 1; mask <<= 1; } unsigned fn = 1, fn1 = 1, gn, gn1; while (mask > 1) { mask >>= 1; gn = fn; gn1 = fn1; if (n & mask) { fn = gn1 * gn1 + gn * gn; fn1 = gn1 * gn1 + 2 * gn * gn1; } else { fn = 2 * gn * gn1 - gn * gn; fn1 = gn1 * gn1 + gn * gn; } } return fn; } int main() { for (int i = 0; i < 20; i++) cout << fibonachi(i) << " "; return 0; } 

UPD 「長い」演算を考慮した漸近の推定値を追加