🤷 🛠️ 🕴🏿 サイバーパンク、マトリックス、キャンバス 🤘🏻 😈 🤽

I.はじめに。

むかしむかし、サイバーパンク小説のエピソードが私の記憶に落ちました。あるヒーローが別のスクリーンを表示し、その上でピクセルが互いにすばやく置き換えられます。各画面の状態は特定の数字で表され、プログラムは徐々にオプションを通過します。

「戦争と平和」、「モナリザ」、「ムーンライトソナタ」の最初のバー、有名な方程式の独創的な解決策、人の写真、このHabrページ、メッセージからのページ過去の未知の出来事や未来の詳細な予測について。

それ以来、私は定期的に接線方向に何かをしようとしましたが、Perlにはいくつかの小さな工芸品がありました。そして最近、JavaScriptで似たようなことをしたかったのです。

II。販売条件。

このような列挙とそのグラフィック表示の実装は簡単です。使用可能なスケールは非常に小さくなります。

簡単にするために、画面上の各ポイントは2つの状態（白と黒）で表され、数字の2進表現の0と1に対応するとします。連続するポイントの座標は、番号内の番号の順序位置に対応します。

現在、JavaScriptでは、計算の精度を保持する最大整数は2の53 Math.pow(2,53) == Math.pow(2,53) + 1はtrue Math.pow(2,53) == Math.pow(2,53) + 1 true 。この数は、54のバイナリ位置で表されます。

 0b100000000000000000000000000000000000000000000000000000 0x20000000000000 9007199254740992

数は、わずか9 x 6ピクセルのマトリックスで回答されます。私のコンピューターが1秒あたり約5,000万回の操作を実行できるとします。マトリックスのすべてのオプションを並べ替えるには、大まかな見積もりが必要になります

Math.pow(2,53) / 50000000 / 60 / 60 / 24 / 365約6年。

より強力なコンピューターであれば、必要なものは少なくなりますが、そのような最高速度で検索を分析することはできません。毎秒25フレームの従来のブロードキャスト周波数で、マトリックス状態が互いに成功するとします。次に、視覚的な速度で2次元の白黒の小さな現実のすべての状態を整理するには、1,428,082年が必要です。

それでも、そのようなものを作成することは興味深いです。上記の最大数はこれにはあまり便利ではありません。左上の点が1つになると（黒で塗り直されると）、この行列には他に何も描画できないからです。そのため、顕微鏡写真の極端な上部と左側の線を完全に使用することはできません。そのため、マトリックスを黒で完全に埋めることができ、任意の状態を取り、比較的比例した形状をとることができる、少し小さい数を取りましょう。これは、最大50のバイナリ次数を持つ10 x 5のマトリックスになります。

 parseInt( "1111111111" + "1111111111" + "1111111111" + "1111111111" + "1111111111" , 2)

 0b11111111111111111111111111111111111111111111111111 0x3ffffffffffff 1125899906842623

それ以降のすべての実装は、Chrome、Firefox、Opera、およびSafariの最新バージョンで正常にテストされています。残念ながら、9番目のIEでテストすることはできません。8番目の例では、キャンバスを使用しなくても動作します。

任意のマトリックスを保存し、必要に応じて編集し、ローカルで実行できます。

さらにすべてが幼稚園のようなものであることを理解しています。したがって、私は他の人のおもちゃで遊ぼうとする人道主義的な考え方を持つ人に寛大さを求めます。これはすべて（わずかに形而上学的な）楽しみのためです:)

III。順次行列。

マトリックスは非常に小さいため、ピクセルグラフィックに実装するのはあまり便利ではないため、スケーリングを簡単かつ簡単にするために、色が変化する5つのセルを持つ単純な10行5列のテーブルを作成します。最初の順序は右下隅にあります。

手始めに、私はそのようなマトリックスのために数字コンバーターへのチャートを書きました。セルをマウスでクリックするたびに色が変わり、それに応じて数字の順序が1から0に切り替わります。プレートの上に、数値自体が10進形式で表示されます。ピクセル単位のセルサイズは、ページアドレスのscaleパラメーターで設定できます。

変換器

状態の連続的な変化を伴う行列自体を記述することは残っています。これは同じテーブルですが、動作が異なります。プレゼンテーションの明瞭さからページの邪魔にならないように、このクラフトと次のクラフトのコントロールは、マウスとURLのパラメーターの間で分散されます。

マトリックスには、次のデフォルトを持つ3つのパラメーターがあります。

scale=10すでに述べたピクセル単位のセルサイズ。
fps=25秒あたりのフレームレート。
start=1検索を開始する番号。

マウスをクリックするたびに数が1つ増え、マトリックスの状態が変わります。 Ctrlキーを押したままにすると、自動検索が開始/停止します。現在の番号は、ドキュメントのタイトル（ウィンドウ、タブ）に表示されます。

10x5シリアルマトリックス

たとえば、グラフィックユニットを表示する状態の間で：

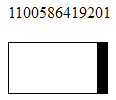
およびグラフィックデュースを表示する状態：

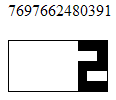
7697662480391 - 1100586419201 = 6597076061190フレームを7697662480391 - 1100586419201 = 6597076061190ます。 FPSでは、デフォルトは約8368年の熟考です:)

ポイントが高く左にあるほど、表示されるまでに時間がかかります。

たとえば、メインの質問に対するメインの回答が少しずつ他の回答に変わる様子を見ることができます。

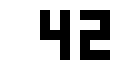
IV。ランダム行列。

1. 1つの番号。

順次列挙行列は、ランダムな値を並べ替える行列に変換できます。初期数のパラメーターは意味を失います。そうでなければ、すべてが同じままです（デフォルトでフレームレートを1秒あたり1に減らした場合を除き、それ以外は判読不能なちらつきです）。

ランダムな状態の1つ、奇妙なことに-完全な文字Aを使用：

ランダム10x5マトリックス

2.数字のセット。

マトリックスの現実をどういうわけか多様化するために、1つの数値を列挙するという境界を越えます。サイズに制限のないマトリックスを作成します。それらの状態は、さまざまな原則に従って、一連の乱数によって設定されます。キャンバスを使用して実装します。

a。ランダムな画像全体。

ここでは、マトリックスの各フレームは完全に異なります。フレームの各ポイントは、1つの乱数で与えられます。デフォルトのパラメーターを分析してみましょう（前後のリンクには明確にするためにこれらのパラメーターが含まれています：パラメーターを指定しない場合、これらの設定が使用されます）。

w=400ピクセル単位のマトリックス幅
h=300ピクセル単位のマトリックスの高さ
fps=1フレームレート

前と同様に、1クリックで1フレームが置き換えられます。 Ctrlキーをクリックすると、ランダムな状態変更が開始されます。しかし、現在、いくつかの機能が追加されています。

新しいタブまたは新しいウィンドウで中マウスボタンをクリックすると、突然何らかの理由で画像を保存する必要がある場合、PNG形式のマトリックスのコピーが開きます（ちなみに、その後のすべてのイラストはそのように取得されます）。

Shiftながら左クリックすると、画像の色深度が切り替わります（白黒、グレースケール、カラーモード）。 Shift+AltキーをShift+Altすると、切り替えは逆の順序で実行されます。

もちろん、各ポイントのランダム性は、大部分の州で未設定のテレビの画面のようなグラフィックノイズが発生することを意味します。結局のところ、交替はそのような空間に比較的均等に分配されます。しかし、豊かな想像力と繊細な知覚を持つ人々は、このノイズの中に興味深いプロットを見ることができたり、気まぐれな関連性のためにエキサイティングな何かを思いがけず思い出すことができます。

ランダム画像

b。ランダムポイント。

このタイプのマトリックスでは、ランダムポイントが一定の背景に連続して追加されます。もう1つのパラメーターを紹介します。

bg=w背景色（w-白（白）、b-黒（黒））。別のカラーモードも追加され、現在4つのモードがあります：単色（反対側の背景に黒または白のドット。遅かれ早かれキャンバス全体を塗りつぶすことができ、状態は視覚的に変化しなくなります）および前の3つのモード（塗りつぶしは発生しません。白黒モードでは、以前の状態を新しい状態で塗りつぶすことができます）。

黒の背景にグレースケールまたは色で表示されるドットは、異なる明るさの星に点火するのに似ています。

また、背景を白にしてアニメーションを開始し、ページを拡大すると、時間の経過とともに子供向け雑誌でよく見られるゲームをプレイできます。ドットをつなげて写真を作ります。真の姿は事前にはわかりません。

ランダムポイント

c。ランダムな線。

この種のマトリックスでは、ランダムな線が常に背景に追加されます。私たちは学校で別の似たようなゲームをよくプレイしたことを覚えています：空白のシートを取り、一人のプレイヤーが見ずに任意のパターンを描き、次に残りのプレイヤーが見る画像を丸で囲みます。このゲームの初期フィールドに似たパターンがマトリックスに表示されます。

さらに2つの要素が、以前のランダム要素（ポイント座標と色）に追加されます。新しいパラメーターがそれらを担当します。

lines=r種類（3つの値を取ることができます：s-直線のみ、c-曲線のみ（曲線）、r-線と曲線のランダムな交互（ランダム）;曲線をセグメントの開始点と終了点の2つのランダムな点に描画する場合ベンドを制御する2つのランダムポイントが追加されます-ベジェ曲線の通常のパラメーター）;

traverse=r描画の方法（3つの値も取ります：y-紙から手を離さずに描画（yes）、n-毎回新しいランダムなポイントで線を開始します（no）、r-連続的な継続によるランダムな分離の交互（ランダム））

以前の4つのカラーモードはここに残ります。

ランダムライン

d。ランダムな数字。

次に、線を閉じて塗りつぶします。ランダムな「ストローク」が得られます。トラバースパラメータはその意味を失いますが、3つの新しいランダム係数とそのパラメータが追加されます。

alpha=y色の透明度のレベルをランダムに変更します（y（yes）またはn（no）の2つの値、それぞれ透明度を使用するかどうか）。透明度を使用する場合、色深度の最初の3つのモード（モノクロ、白黒、グレーの濃淡）は互いに非常に似たものになります。

minnodes=3の最小ノード数

maxnodes=10図のノードの最大数。

デフォルトでは、制限は3（数字が機能しないため、少なく設定しても意味がありません）から10（この上限はコードで編集できます）に設定されます。形状パラメーターは、すでに図形の形状に大きな影響を与えています（それぞれ、ポリゴンまたはより複雑な形状が取得されます）。数字はしばしば自己交差するため、さまざまなスペースで塗りつぶすのは難しいことに留意してください。

以下は、アルファチャネルを使用せずに透明度を使用した、異なる背景のさまざまなカラーモードの例です。