前の
記事で、コピュラの理論的根拠を説明しました。 私自身は学生だったので、理論的な装置の最良の説明がその実用化の例になり得ることを知っています。 したがって、この記事では、コピュラを使用して、いくつかのランダム変数の相互依存関係をモデル化する方法を示します。

再び少し理論
すでに述べたように、多くのコピュラは、2つだけでなく複数の値の依存関係を一度に反映できます。 もちろんこれは良いことですが、標準のコピュラはある程度の対称性を意味します。つまり、すべてのペアワイズ依存関係は同じパターンを持ちます。 同意する、これは常に真実ではない。 この問題を克服するために、興味深い非常に明白な(数学的分析でこの単語の背後にある苦痛がどれだけ隠されているか)方法が提案されました-結合コピュラを2次元コピュラのセットに分割します。 n個の変数に対して、

ペアワイズ関係。 つまり、非常に多くのペアワイズコピュラを決定する必要があります。 4つの量の共同分布密度は次のように表現できることを示します。
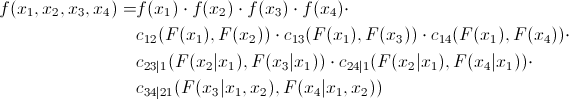
少しの証拠まず、いくつかの数量の分布密度は次のように表現できることを思い出してください。

また、コピュラの定義から、次のことがわかります。

これは次のように表現できます。

2次元の場合、次のようになります。

そして、これを最初の式と組み合わせると、次のようになります。

この例を3次元のケースに拡張できます。

前の式と組み合わせると、次のようになります。

したがって、最初の方程式のすべての要素は、対になったコピュラと周辺密度の積として表現できることがわかります。
パーティションを表すいくつかの方法があり、上記は正規のicalと呼ばれます(私は心から謝罪しますが、数学的な文脈で「正規のvine」の確立された翻訳を見つけられなかったため、直接翻訳を使用します)。 グラフィカルに、最後の方程式は次のように表すことができます。

3つのツリーは、4次元コピュラのパーティションを表します。 左端のツリーでは、円は周辺分布であり、矢印は2次元のコピュラです。 モデリングの責任者としての私たちのタスクは、すべての「矢印」を設定すること、つまりペアワイズコピュラとそのパラメーターを決定することです。
次に、D字型のつるの式を見てみましょう。
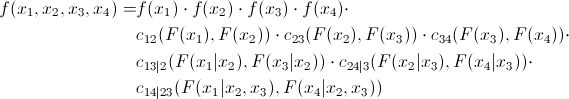
およびそのグラフィカル表現
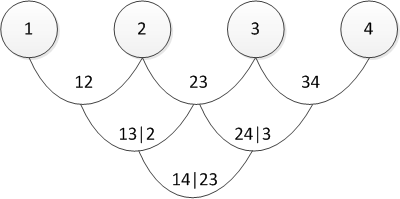
実際、正準およびD-vinesは、ペアワイズ依存関係が決定される順序でのみ異なります。 「順序をどのように選択しますか?」またはそれに相当する「どのぶどうの木を選択する必要がありますか?」と尋ねることができます。実際には、最大の関係を示すペアから始まります。 後者は
ケンドールのタウによって決定されます。 心配しないでください-直接の実際的な例を示すと、すべてが後で明らかになります。
コピュラの定義の順序を決定したら、接続を決定するために使用するコピュラ(ガウス、スチューデント、ガンベルなど)を理解する必要があります。 原則として、正確な科学的方法はありません。 誰かが「アーカイブされた」量の分布のペアのグラフを見て、目でコピュラを決定します。 誰かがChi-graphics
を使用しています (
ここでは、それらの使用方法が書かれています )。 熟達の問題と研究のための広大な分野。
ペア関係で使用するコピュラを決定したら、それらのパラメータを決定する必要があります。 これは、次のアルゴリズムを使用した数値最尤法(数値MLE)によって行われます。
正規のつるパラメーターを評価するための擬似コードLog-likelihood=0; for i = 1:n v(0,i) = x(i) end for for j = 1:n-1 for i = 1:nj Log-likelihood = Log-likelihood + L(v(j-1,1), v(j-1,i+1), param(j,i)); end for if j == n then break end if for i = 1:nj v(j,i) = h(v(j-1,i+1), v(j-1,1), param(j,i)); end for end for
D-vineパラメーターを評価するための擬似コード Log-likelihood=0; for i = 1:n v(0,i) = x(i); end for for j = 1:n-1 Log-likelihood = Log-likelihood + L(v(0,i),v(0,i+1), param(1,i)); end for v(1,1) = h(v(0,1),v(0,2), param(1,1)) for k = 1:n-3 v(1,2k) = h(v(0,k+2), v(0,k+1), param(1,k+1)); v(1,2k+1) = h(v(0,k+1), v(0,k+2), param(1,k+1)); end for v(1,2n-4) = h(v(0,n), v(0,n-1), param(1,n-1)); for j = 2:n-1 for i = 1:nj Log-likelihood = Log-likelihood + L(v(j-1,2i-1),v(j-1,2i), param(j,i)); end for if j == n-1 then break end if v(j,i) = h(v(j-1,1), v(j-1,2), param(j,1)); if n > 4 then for i = 1:nj-2 v(j,2i) = h(v(j-1,2i+2),v(j-1,2i+1),param(j,i+1)); v(j,2i+1) = h(v(j-1,2i+1),v(j-1,2i+2),param(j,i+1)); end for end if v(j,2n-2j-2) = h(v(j-1,2n-2j),v(j-1,2n-2j-1),param(j,nj)) end for
これらは対数尤度関数を計算するためのアルゴリズムであり、ご存じのように最大化する必要があります。 これは、さまざまな最適化パッケージのタスクです。 ここでは、「コード」で使用される変数について少し説明する必要があります。
xは、サイズT x nの「アーカイブされた」データのセットです。xは、間隔(0,1)に制限されています。
vは、サイズT x n-1 x n-1の行列で、中間データがロードされます。
param-対数尤度を最大化する、対になったコピュラのパラメーター。
L(x、v、param)=
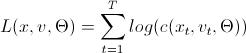
h(x、v、param)=
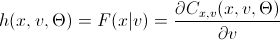
彼らの計算で論文を台無しにするファンは、次のネタバレを開かないかもしれません。そこで、主要なコピュラのh関数を導入しました。
対数尤度関数を最大化するコピュラのパラメーターを見つけたら、初期データと同じ関係構造を持つランダム変数の生成に進むことができます。 このために、アルゴリズムもあります。
モデル推定アルゴリズムを使用して取得したパラメーターを使用して、n個の変数を生成します。 このアルゴリズムをT回実行し、n行の行列Tを取得します。このデータは、元のデータと同じ関係パターンを持っています。 以前のアルゴリズムと比較した唯一の革新は、逆h関数(h_inv)です。これは、最初の変数に対する条件付き分布の逆関数です。
繰り返しますが、長い計算からあなたを救います:
それは基本的にそれです。 そして今、約束された...
実用例
1.たとえば、私はポートフォリオの毎日のVaRを計算するように言われた小さな銀行員を演じることにしました。 2012年1月1日の構内および私のポートフォリオには、3M(MMM)、Exxon Mobil(XOM)、Ford Motors(F)、Toyota Motors(TM)の4社の株式が均等に配分されています。 良いah-tishnikiに悩まされ、過去6年間サーバーから価格履歴をアンロードできるようになったので、彼らには時間がありません(1月1日、庭で働いています。 2005年1月3日から2011年12月31日までの毎日の価格履歴を取得しました。 結果のマトリックスは1763 x 4です。
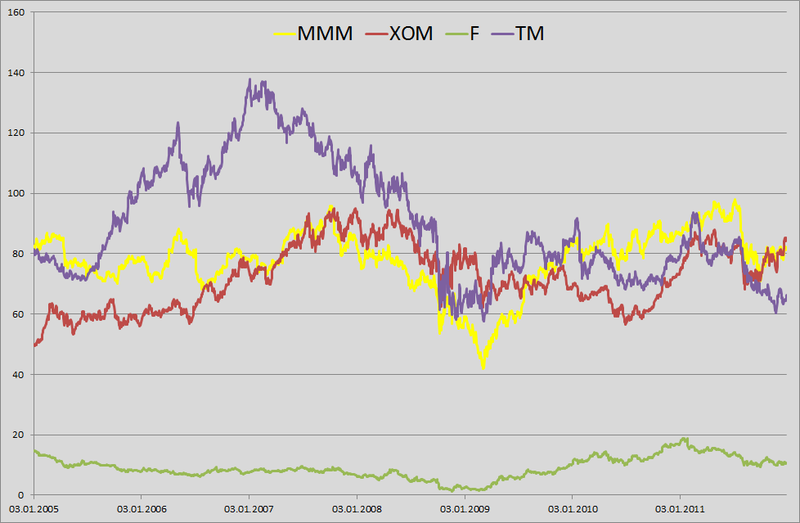
2. log-retarを見つけました:
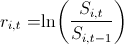
ペアワイズ分布を構築しました。
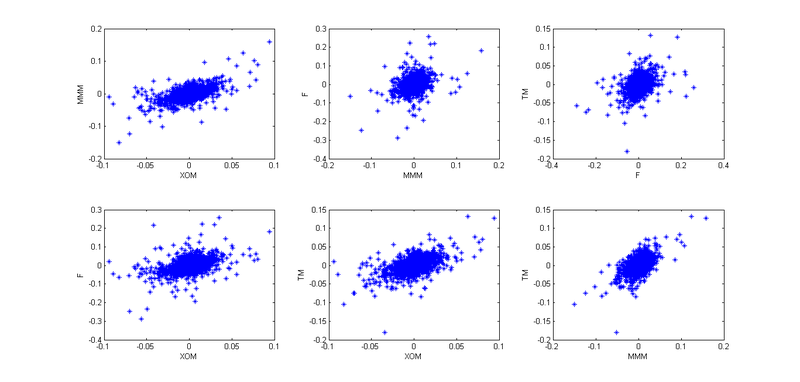
さて、全体像を提示します。
3.それから、私は金融に関する講義と私たちが私たちに打ち込まれた方法を思い出しました-「みんな、リターンが正常に配布されているという事実はゴミです。 実生活ではそうではありません。」 リターンがNIG(Normal Inverse Gaussian)に従って分布しているという仮定を使用すべきかと考えました。 調査によると、この分布は経験的データとよく一致しています。 しかし、VaR計算モデルを考え出し、それを履歴データでテストする必要があります。 2番目の瞬間のクラスタリングを考慮しないモデルは、悪い結果を示します。 その後、アイデアが生まれました-GARCH(1,1)を使用します。 このモデルは、3番目と4番目の分布の瞬間を非常によく把握し、さらに2番目の瞬間のボラティリティを考慮します。 だから私は私のリターが次の法律に従うことを決めました

。 ここで、cは履歴平均、zは標準正規分布確率変数、sigmaはすでに独自の法則に従います。
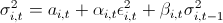
。
4.だから、今、これらの4つの株の相互依存を考慮する必要があります。 最初に、経験的コピュラを使用して、「アーカイブされた」観測値のペアの依存関係をプロットしました。
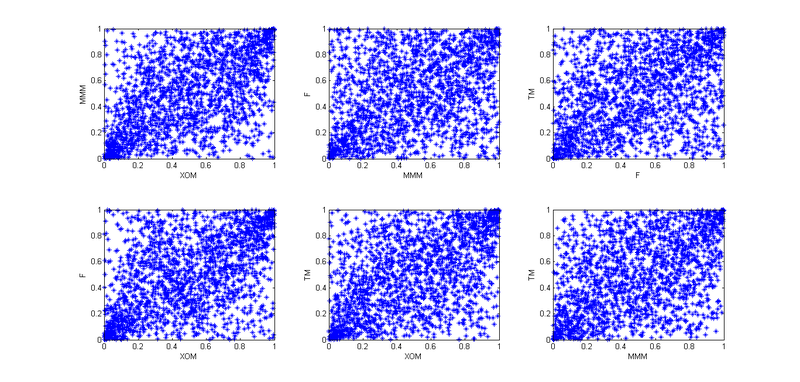
今日は1月1日で、私は怠け者であるため、ここでのパターンはすべて学生のコピュラに似ていると判断しましたが、相互依存性をよりよく伝えるために、4次元のコピュラを使用せずに、6つの2次元のコピュラに分割することにしました。
5.対になったコピュラに分割するには、プレゼンテーションの順序(標準またはD-vine)を選択する必要があります。 このために、相互依存のレベルを決定するためにケンドールのタウを数えました。
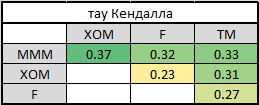
MMMが他のすべての企業と最も強い関係を持っていることは簡単にわかります。 これにより、ブドウの選択が決まります-正規。 なんで? PageUpを数回押して、グラフィック表示を確認します。 最初のツリーでは、すべての矢印は1つのノードから来ています。これは、ある会社が最も強い接続を持っているまさにその状況です。 最後のテーブルのケンドールの高いタウが異なる行と異なる列にある場合、D-vineを選択します。
6.表示の順序と必要なすべてのペアワイズコピュラを決定しました。パラメータの評価を開始できます。 正規のvineのパラメータを評価するために上記のアルゴリズムを適用すると、必要なすべてのパラメータが見つかりました。
7.ここで、バックテストのコンテキストでこれがどのように発生したかを少し説明します。 私のモデルがVaRをどの程度妥当と考えるかを確認するために、過去にどのように処理されたかを確認したかったのです。 これを行うために、私は彼女にわずかな有利なスタートを与えました-500日、そして501日から始めて、私は翌日のリスク指標を考慮しました。 コピュラのパラメーターを手元に持って、10,000の4つの均等に分布した値を生成し、それらから4つの正規分布値(ノイズ)を取得し、この例の3点から逆行を計算する式に代入しました。 そこで、過去のデータ(これはMatlab関数ugarchとugarchpredの組み合わせによって行われた)と履歴平均を使用して、GARCH(1,1)モデルによるシグマ予測を挿入しました。 このようにして10,000株の株式を受け取り、ポートフォリオの10,000株を受け取りました。株式の算術平均を取ります。
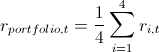
(等しいシェアとログリンクがあるため、そうする権利があります)。 次に、それぞれしきい値レベルの99.5%、99%、および95%の50番目、100番目、および500番目の値のソートおよび選択。 このようにして残りの1263日間のメトリックのリスクを計算すると、レベルの内訳の美しいグラフと統計が得られました。
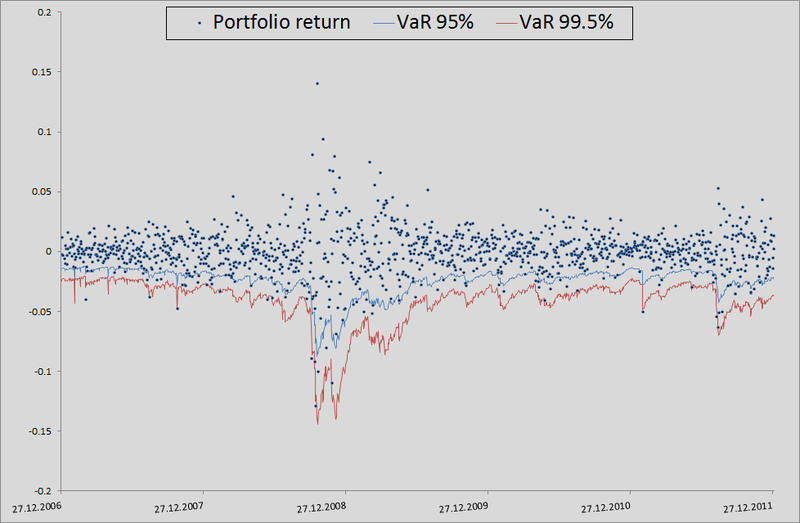
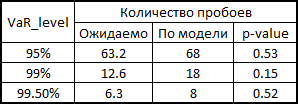
VaR内訳統計のp値の読み方1995年、同志KupichはVaR計算モデルの信頼性を計算するための式を提案しました。

ここで、xはモデルに応じた内訳の数、Tはテストの数(= 1263)、pは内訳の予想シェア(この場合は0.5%、1%、5%)です。
帰無仮説によれば、これらの統計には1つの自由度を持つ
カイ二乗分布があります。 統計を見つけたら、そのp値を簡単に計算できます。
原則として、精度を向上させるにはまだ多くのことがあります。 しかし、一般的に相互依存性を考慮せずにモデルをベンチマークとして使用する場合、一般的に継ぎ目があります。
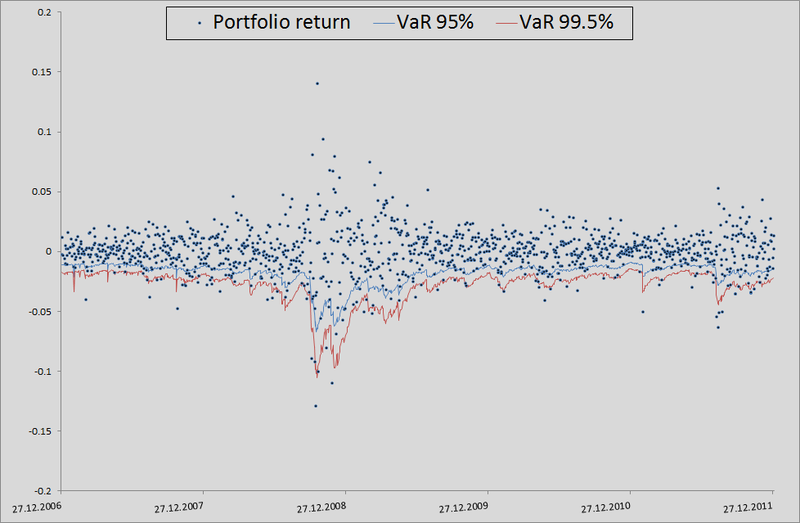
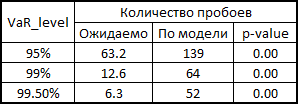
正直に言うと、相関と生成されたノイズを使用して多次元正規分布からリトレンを計算した場合のモデルの動作を示す必要があります。
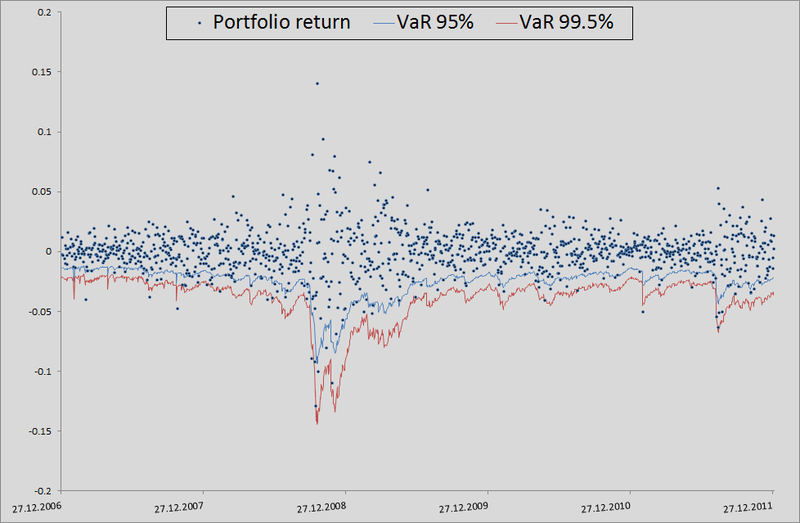
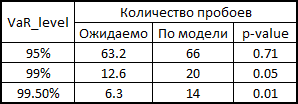
ご覧のとおり、VaR 95%の場合、このモデルは私たちのモデルよりも優れています。 しかし、さらに悪いことに、すでに述べたように、正規分布はテールをキャッチしません。
一般に、コピュラを使用できますが、これは賢明に行う必要があります。 それらは相互依存性を考慮するより多くの機会を提供しますが、正確なモデルと同様に、ここで注意する必要があります-仮定を逃し、標準モデルよりも悪い結果を得る可能性があります。
PS私はしばしば私の後ろに舌で縛られていることに気づいたので、テキストのそのような瞬間を私に指摘していただければ嬉しいです。 私は考えをできるだけ明確に表現しようとしましたが、常に成功するとは限りません。