ガウスぼかしフィルター(Photoshopで広く知られている「ガウスぼかし」)は、単独で、または他の画像処理アルゴリズムの一部として使用されることがよくあります。 次に、
無限インパルス応答を持つフィルターを使用して、ぼかし半径に依存しない速度でぼかしを可能にする方法を説明します。
メソッドの説明は
英語です。 しかし、ロシア語での情報はありません。 さらに、いくつかの変更を加えました。
したがって、元の画像が明るさ
x (
m、n )で与えられるようにします。 半径
rのガウスぼかしは、式によって計算されます
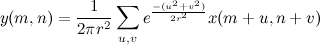 u
uおよび
vの合計制限は、プラスまたはマイナスのいくつかのシグマとして選択できます。 半径
rのピクセルごとのO(
r 2 )演算の次数のアルゴリズムの複雑さを与えます。 大きな
rおよびマルチメガピクセルの画像の場合、クールすぎませんか?
最初の加速は、ガウスぼかしの分離可能性プロパティを提供します。 つまり、各行の
x軸に沿ってフィルター処理し、各列の結果のイメージを
yでフィルター処理して、ピクセルごとのO(
r )操作の複雑さで同じ結果を得ることができます。 すでに良い。 このプロパティも使用するため、さらにすべての引数は、
x (
n )を持つ
y (
n )を取得する必要がある1次元の場合になります。
無限のインパルス応答を持つフィルターはこれに役立ちます。 フィルターの考え方は次のとおりです
。y (
n )の値は、次の式によって再帰的に計算されます。
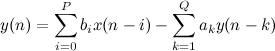
ここで
、a kと
b iはいくつかの計算された係数であり、
n <0の
y (
n )と
x (
n )はゼロであると仮定されます。
b iに依存する式の部分は、
有限カーネルによる単純な畳み込みに縮小され
ます 。 フィルターの高速化を検討するため、
P = 0の場合のフィルターを探します。つまり、単一の係数
b 0を考慮し
ます 。
念のため、線形フィルター(およびIIRフィルターも線形)は、ポイント0で1、その他すべてのポイントで0に等しいデルタ関数への応答によって完全に特徴付けられることを思い出させてください。 そのような関数に応答
するときに係数
aに依存する部分は、発散して無限大になるか(これを避けたい)、または美しい衰退尾部を与えます。 たとえば、次のように:

ガウスのように聞こえますか? まあ、はい、何かがすでに存在しますが、どういうわけかそれは厄介に見えます。 したがって、アルゴリズムの考え方は次のようになります。1つの方向(
0〜n maxのサイクル)でフィルターし、次に同じ係数で反対方向(
n max〜0 )の結果にフィルターします。 数学的には、厳密に対称な曲線を取得する必要があります(したがって、最初に前後にフィルターをかけても、逆にフィルターをかけても問題はありません)。 少し先に実行すると、これを逆の順序でフィルタリングするとどうなりますか。
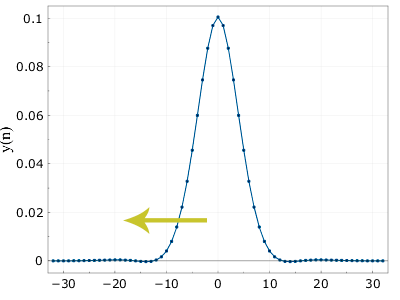
こっち ほぼ必要なもの。 ほぼ、実際、もちろん、まったくそうではないからです。 曲線はわずかに負の領域に入り、一般に正確なガウス曲線とは異なります。 しかし、ほとんどのアプリケーションでは、これはすべて受け入れられます。さらに、絶対に確実に考慮する必要がある場合は、
Qフィルターの次数を増やすことができます。
したがって、フィルタ係数
aを計算することは残ります。 さらに、すべての式は
Q = 3の場合に適用されます。
一般に、フィルターはいわゆる
伝達関数を使用して研究
されます 。 希望する人はそれが何であるかを読むことができます、そして初心者にとってはそれが存在し、特定のプロパティを持っているだけで十分です。 線形フィルターのこの関数の一般的な見方は次のとおりです。
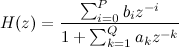
または、
Q = 3、
P = 1の場合:

分子と分母に多項式があるので、それらを因数分解できます。 一般的な場合、分子はゼロを与え(この場合ゼロはありません)、分母は極を与えます:
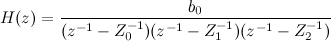
この例では、1 /
Z 0、1 /
Z 1、1 /
Z 2です。 極
は 、フィルターの係数
a kを一意に決定することに注意してください(すべてのIIRフィルターは、通常、極ではなく、極を通して検索されます)。 ところで、極で係数を取得するのは、逆の場合よりも簡単です(このため、多項式を乗算する必要があり、逆の場合は、電力方程式を解きます)。
私たちにとって有用な最も重要な理論的仮定:複素極が単位円の内側にある場合、つまり 1未満のモジュロ(または同じことです。Z0、
Z 1 、
Z 2の逆値は単位円の外側にあります)、フィルターは安定し、結果は無限になりません。
また、任意の複素共役に
Z 0 、
Z 1 、および実
Z 2 (ここでもすべてが1つ以上のモジュロ)の名前を付けることで、それらからフィルターを構築できることに注意してください。 製品では、すべてが厳密に実数の係数
aに変わります。
係数
b 0は、フィルターの「体積係数」として機能します。
したがって、問題は3つの係数
Z 0 、
Z 1 、
Z 2の決定に限定されました。 繰り返しますが、2つは複素共役であり、3つ目は実数なので、最初の実数部と虚数部、および3つ目の実数部を見つける必要があります。 つまり、3つの実数:実数(
Z 0 )、im(
Z 0 )、
Z 2これらの3つの数値は、必要なフィルター半径に関して表現する必要があります。 実際には、2以上の
rを考慮することは理にかなっていることに注意してください。値が小さいほど、乗算によるフィルタリングが高速になります。
さらに、「再帰的ガウス微分フィルター」という作品とは少し違った方法で進みました。 そこで、
r = 2のケースを他のすべてのケースに拡張し、2〜2048のすべての半径に最適な係数を指数ステップで決定しました。 最大差モジュラスを最小化することにより、最も近い曲線を検索する最適化アルゴリズムを作成しました。 追加の条件は、全エネルギーのフィルターによる保存でした。 関数
x (
n )= constが自身に渡され、条件が与えられるように
b 0 = 1-(
a 1 +
a 2 +
a 3 )
さまざまな最適化アルゴリズムを試しましたが、最良のものはわずかに修正された遺伝的アルゴリズムを示しました。 (おそらく、最適化について別のメモを書くことができます)。
興味のある方は、
Googleスプレッドシートで結果を確認できます。
r = 2の場合、結果は作業中のデータとは異なることがわかります。 なぜだかとは言えませんが、私の計算によると、係数の誤差は40%小さくなります。
さらに、私は手紙ではなく記事の精神を使用し、データの検索を始めました。
実数(
Z 0 )= cos(
W (
r )/
r )* e
A( r )/ rim(
Z 0 )= sin(
W (
r )/
r )* e
A( r )/ rZ 2 = e
B ( r )/ rつまり 次に、3つの同様の関数を選択する必要があります。それぞれの関数は定数で制限される傾向があります。 関係としての機能を探していました
(
k 3 r 3 +
k 2 r 2 +
k 1 r +
k 0 )/
r 3そして、
Wolfram Mathematicaを使用して、最も簡単な方法で係数を選択しました。 ところで、テーブルからのデータのグラフを注意深く調べると、関数がやや鋸歯状の構造を持っていることがわかります。 したがって、近似するとき、精度は少し低下しますが、実際には少し-テーブルの値は、多項式で得られる値よりも10%小さい誤差を与えます。
よくここに。 何を考慮すべきか、何を考慮すべきかについてすでに混乱している人のために、係数を計算するためのCの最終関数コードを提供します。
int gaussCoef(double sigma, double a[3], double *b0) { double sigma_inv_4; sigma_inv_4 = sigma*sigma; sigma_inv_4 = 1.0/(sigma_inv_4*sigma_inv_4); double coef_A = sigma_inv_4*(sigma*(sigma*(sigma*1.1442707+0.0130625)-0.7500910)+0.2546730); double coef_W = sigma_inv_4*(sigma*(sigma*(sigma*1.3642870+0.0088755)-0.3255340)+0.3016210); double coef_B = sigma_inv_4*(sigma*(sigma*(sigma*1.2397166-0.0001644)-0.6363580)-0.0536068); double z0_abs = exp(coef_A); double z0_real = z0_abs*cos(coef_W); double z0_im = z0_abs*sin(coef_W); double z2 = exp(coef_B); double z0_abs_2 = z0_abs*z0_abs; a[2] = 1.0/(z2*z0_abs_2); a[0] = (z0_abs_2+2*z0_real*z2)*a[2]; a[1] = -(2*z0_real+z2)*a[2]; *b0 = 1.0 - a[0] - a[1] - a[2]; return 0; };
それだけです! 次に、コード自体を記述する必要があります。 もちろん、計算はフロートで行う必要がありますが、最新のコンピューターは浮動小数点数を(特にsseを使用して)かなり迅速に計算します。 ちなみに、Intelプログラマーは、ベクトルプロセッサ命令用にGauss-IIRフィルターを最適化するように注意し
ており、既に記事全体を書いています 。 確かに、彼らはそこにわずかに異なる方法を検討していますが、主な最適化方法はよく説明されています。
最後に、何が起こったのか例を示すことができます:

絵は実際には「正直な」ものと違いはありません。 ただし、Photoshopで開いて注意深く調べると、違いを見つけることができます。
PSこれは本当にHabréでの私の最初の投稿です。何かを見逃す可能性があります。 ご質問がある場合は、コメントでお答えします。