乱数ジェネレーターの脆弱性に関する記事は、しばしばHabréとネットワークに掲載され始めました。 このトピックは非常に広範囲で、暗号化の主要なものの1つです。 カットの下には、AからZまでの乱数の説明があります。この記事は、1つの西洋のブログからの一連の記事の無料翻訳と著者の個人的な追加の結果です。 主な目標は、フィードバックを得て知識を共有することです。

はじめに
乱数ジェネレーターは、Webセキュリティの重要な部分です。 用途の小さなリスト:
- セッションジェネレーター(PHPSESSID)
- キャプチャテキストの生成
- 暗号化
- パスワードを保存するための不可逆的なソルト生成
- パスワードジェネレーター
- オンラインカジノでカードを配布する手順
数字のランダムなシーケンスを非ランダムなものと区別する方法は?
1、2、3、4、5、6、7、8、9の数字のシーケンスがあるとします。 彼女はランダムですか? ランダム変数には厳密な定義があります。 ランダム変数は、実験の結果として多くの値の1つを取る量であり、測定前のこの量の1つまたは別の値の出現は正確に予測できません。 しかし、答えるのに十分な情報がないため、質問に答えることは役に立ちません。 ここで、これらの数字がキーボードの一番上の行の1つのセットであることが判明したとしましょう。 「間違いなく偶然ではない」-次の番号を叫び、すぐに名前を付けると、あなたは絶対に正しいでしょう。 シーケンスは、キャラクター間に依存関係がない場合にのみランダムになります。 たとえば、これらのシンボルが樽を宝くじに引き込んだ結果として現れた場合、シーケンスはランダムになります。
もう少し複雑な例またはPi

数字Piの数字列はランダムと見なされます。 ジェネレーターは、Piを表すビットの派生に基づいて、未知のポイントから開始します。 PIは明らかにランダムなシーケンスである
ため、このようなジェネレーターはおそらく
「次のビットのテスト」に合格します。 ただし、このアプローチは、批評的に信頼できるものではありません-暗号解読者がPi番号のどのビットが現在使用されているかを判断した場合、彼はすべての前後のビットを計算できます。
この例では、乱数ジェネレーターにもう1つの制限を課しています。 暗号解読者は、乱数ジェネレーターの動作を予測できないはずです。
擬似乱数ジェネレーター(PRNG)と乱数ジェネレーター(RNG)の違い
エントロピーのソースは、エントロピーを蓄積し、そこから乱数を生成するために乱数ジェネレーター(RNG)が必要とする初期値(初期値、シード)を取得するために使用されます。 PRNGは単一の初期値を使用し、その初期値から擬似乱数が生成されます。RNGは常に乱数を生成し、最初はさまざまなエントロピーのソースによって提供される高品質の乱数値を持ちます。
エントロピーは無秩序の尺度です。 情報エントロピーは、情報の不確実性または予測不能性の尺度です。
RNG = PRNG +エントロピーのソースと言えます。
PRSPの脆弱性
- 数字間の予測可能な関係。
- ジェネレーターの予測可能な初期値。
- 乱数の生成されたシーケンスの短い期間の長さ。その後、ジェネレーターはサイクルになります。
線形合同PRNG(LCPRNG)
暗号強度を持たない擬似乱数を生成する一般的な方法。 線形合同法は、次の式で与えられる、自然数mを法とする線形反復シーケンスのメンバーを計算することで構成されます。
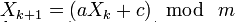
ここで、a(乗数)、c(加数)、m(マスク)はいくつかの整数係数です。 結果のシーケンスはシードX0の選択に依存し、その異なる値に対して、乱数の異なるシーケンスが取得されます。
係数を選択するために、周期の長さを最大化するプロパティがあります(最大長はmです)。つまり、発電機がサイクルを開始する瞬間です[1]。
ジェネレーターにいくつかの乱数X0、X1、X2、X3を与えます。 方程式系が判明

このシステムを解決したら、係数a、c、mを決定できます。 ウィキペディア
[8]によると、このシステムには解決策がありますが、単独で解決したり解決策を見つけることはできませんでした。 この分野で助けていただければ幸いです。
線形合同法の結果の予測
線形合同法の数値を予測するための主なアルゴリズムはPlumsteadのアルゴリズムです。このアルゴリズムの実装は、ここ
[4] (オンラインで起動します)およびここ
[5]で見つけることができます。 アルゴリズムの説明は
[9]にあります。
Javaでの合同メソッドの単純な実装。
public static int a = 45; public static int c = 21; public static int m = 67; public static int seed = 2; public static int getRand() { seed = (a * seed + c) % m; return seed; } public static void main(String[] args) { for(int i=0; i<30; i++) System.out.println(getRand()); }
20の番号をサイトに送信することで
[4] 、次の情報を取得できます。 数字が多いほど、確率が高くなります。
Javaの組み込み乱数ジェネレーターのハッキング
C(rand)、C ++(rand)、Javaなどの多くのプログラミング言語はLCPRNGを使用します。 例として
java.utils.Randomを使用してハッキングする方法を見てみましょう。 このクラスのソースコード(jdk1.7)を見ると、使用されている定数を確認できます。
private static final long multiplier = 0x5DEECE66DL;
java.utils.Randon.nextInt()メソッドは次のようになります(ここではビット== 32)
protected int next(int bits) { long oldseed, nextseed; AtomicLong seed = this.seed; do { oldseed = seed.get(); nextseed = (oldseed * multiplier + addend) & mask; } while (!seed.compareAndSet(oldseed, nextseed)); return (int)(nextseed >>> (48 - bits)); }
結果は、48-32 = 16ビットだけ右にシフトされた次のシードです。 この方法は、切り捨てられたビットと呼ばれ、ブラックボックスでは特に不快です。ブルートフォースに別のループを追加する必要があります。 ブルートフォースを使用してハッキングが発生します。
連続して生成された2つの数値x1およびx2を知っているとします。 次に、2 ^ 16 = 65536のoldseedオプションを反復処理して、式をx1に適用する必要があります。
((x1*multiplier + addend) & mask) << 16
x2に等しくなるまで。 ブルートフォースのコードは次のようになります
import java.lang.reflect.Field; import java.util.Random; import java.util.concurrent.atomic.AtomicLong; public class PasswordCracking { public static final long multiplier = 0x5DEECE66DL; public static final long addend = 0xBL; public static final long mask = (1L << 48) - 1; public static void main(String[] args) { Random random = new Random(); long v1 = random.nextInt(); long v2 = random.nextInt(); long v3 = random.nextInt(); long v4 = random.nextInt(); System.out.println("v1=" + v1 + "\nv2=" + v2 + "\nv3=" + v3 + "\nv4=" + v4);
このプログラムの出力は次のようになります。
v1 = -1184958941 v2 = 274285127 v3 = -1566774765 v4 = 30466408 Seed found: -77657469128792 Set fiend seed and generate random numbers cv1 = 274285127 cv2 = -1566774765 cv3 = 30466408 cv4 = -803980434
最初のシードは見つかりませんでしたが、シードは2番目の数値を生成するために使用されたことを理解するのは簡単です。 元のシードを見つけるには、Javaがシードの変換に使用したいくつかの操作を逆の順序で実行する必要があります。
public static long getPreviousSeed(long prevSeed) { long seed = prevSeed;
そして今、ソースコードで置き換えます
crackingSeed.set(シード);
に
crackingSeed.set(getPreviousSeed(シード));
これで、JavaでPRNGを正常に解読できました。
PHPでPRNG Mersenneツイスターをハッキングする
Mersenne Twister擬似乱数を生成するための別の非暗号化アルゴリズムを検討してください。 アルゴリズムの主な利点は、生成速度と2 ^ 19937-1の巨大な期間です。今回は、phpソースコードバージョン5.4.6の
mt_srand()および
mt_rand()アルゴリズムの実装を分析します。
ファイルの内容/ext/standard/basic_functions.h #define MT_N (624) php_uint32 state[MT_N+1]; php_uint32 *next; int left; unsigned int rand_seed; zend_bool rand_is_seeded; zend_bool mt_rand_is_seeded;
ファイル/ext/standard/rand.cの内容: #define N MT_N #define M (397) #define hiBit(u) ((u) & 0x80000000U) #define loBit(u) ((u) & 0x00000001U) #define loBits(u) ((u) & 0x7FFFFFFFU) #define mixBits(u, v) (hiBit(u)|loBits(v)) #define twist(m,u,v) (m ^ (mixBits(u,v)>>1) ^ ((php_uint32)(-(php_int32)(loBit(u))) & 0x9908b0dfU)) static inline void php_mt_reload(TSRMLS_D) { register php_uint32 *state = BG(state); register php_uint32 *p = state; register int i; for (i = N - M; i--; ++p) *p = twist(p[M], p[0], p[1]); for (i = M; --i; ++p) *p = twist(p[MN], p[0], p[1]); *p = twist(p[MN], p[0], state[0]); BG(left) = N; BG(next) = state; } static inline void php_mt_initialize(php_uint32 seed, php_uint32 *state) { register php_uint32 *s = state; register php_uint32 *r = state; register int i = 1; *s++ = seed & 0xffffffffU; for( ; i < N; ++i ) { *s++ = ( 1812433253U * ( *r ^ (*r >> 30) ) + i ) & 0xffffffffU; r++; } } /* }}} */ /* {{{ php_mt_srand */ PHPAPI void php_mt_srand(php_uint32 seed TSRMLS_DC) { /* Seed the generator with a simple uint32 */ php_mt_initialize(seed, BG(state)); php_mt_reload(TSRMLS_C); /* Seed only once */ BG(mt_rand_is_seeded) = 1; } /* }}} */ /* {{{ php_mt_rand */ PHPAPI php_uint32 php_mt_rand(TSRMLS_D) { /* Pull a 32-bit integer from the generator state Every other access function simply transforms the numbers extracted here */ register php_uint32 s1; if (BG(left) == 0) { php_mt_reload(TSRMLS_C); } --BG(left); s1 = *BG(next)++; s1 ^= (s1 >> 11); s1 ^= (s1 << 7) & 0x9d2c5680U; s1 ^= (s1 << 15) & 0xefc60000U; return ( s1 ^ (s1 >> 18) ); }
php_mt_reloadは、初期化中およびphp_mt_randを624回呼び出した後に呼び出されることに気付くかもしれません。 最後からハッキングを始めましょう。php_mt_rand()関数の最後で変換を逆にします。 (s1 ^(s1 >> 18))を検討してください。 バイナリ表現では、操作は次のようになります。
101101110101111001 11111001110010 s1
00000000000000000010110111010111100111111001110010 s1 >> 18
101101110101111001 01001110100101 s1 ^(s1 >> 18)
最初の18ビット(太字で強調表示)は変更されていないことがわかります。
ビットシフトとxorを反転するための2つの関数を記述します
public static long unBitshiftRightXor(long value, long shift) {
php_mt_rand()関数の最後の行を反転するコードは次のようになります
long value = output; value = unBitshiftRightXor(value, 18); value = unBitshiftLeftXor(value, 15, 0xefc60000); value = unBitshiftLeftXor(value, 7, 0x9d2c5680); value = unBitshiftRightXor(value, 11);
Mersenne Twisterで生成された624個の連続番号があり、これらの連続番号にこのアルゴリズムを適用すると、Mersenne Twisterの完全な状態が得られます。既知の値のセットに対してphp_mt_reloadを実行することで、後続の各値を簡単に決定できます。
ハッキングエリア
壊れるものはないと思うなら、あなたは深く誤解されています。 興味深い分野の1つは、Adobe Flash乱数ジェネレーター(Action Script 3.0)です。 その特徴は、クローズドソースコードとシードタスクの欠如です。 主な関心は、多くのオンラインカジノとオンラインポーカーでの使用です。
ドルの為替レートから毎日のトラフィックに費やされる時間まで、数字のシーケンスは多数あります。 そして、そのようなデータでパターンを見つけることは簡単な作業ではありません。
擬似乱数ジェネレーターの分布の設定
任意のランダム変数に対して、分布を指定できます。 例えばカードを使って移動すると、エースを9よりも頻繁に落とすことができます。 以下は、三角分布と指数分布の例です。
三角分布
C99の言語で三角分布の確率変数を生成する例を示します
[7] 。
double triangular(double a, double b, double c) { double U = rand() / (double) RAND_MAX; double F = (c - a) / (b - a); if (U <= F) return a + sqrt(U * (b - a) * (c - a)); else return b - sqrt((1 - U) * (b - a) * (b - c)); }
この場合、ランダム変数rand()を取り、三角分布関数に基づいて分布を設定します。 パラメーターa = -40、b = 100、c = 50の場合、10,000,000測定のグラフは次のようになります。
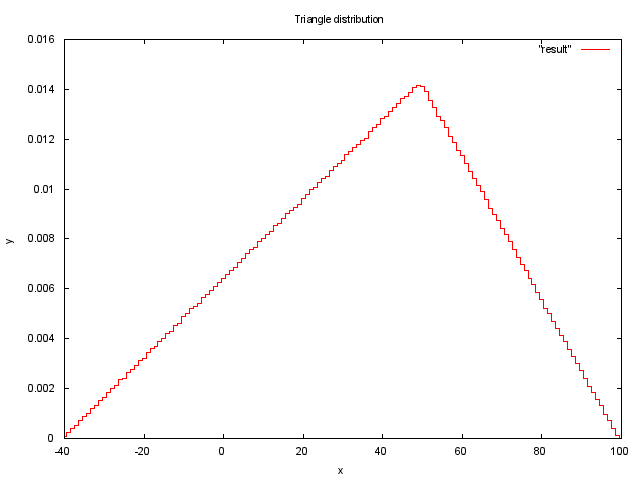
指数分布
指数関数的に分布するランダム変数のセンサーを取得するとします。 この場合、F(x)= 1-exp(-lambda * x)。 次に、方程式y = 1-exp(-lambda * x)の解から、x = -log(1-y)/ lambdaを取得します。
最後の式の対数の下の式は、間隔[0,1)で均一な分布を持っていることに気付くことができます。これにより、次の式に従って別の分散シーケンスも取得できます。x = -log(y)/ lambda (ランド())。
PRNGテスト
一部の開発者は、使用する生成方法を隠したり、独自の方法を考え出した場合、これで保護に十分であると考えています。 これは非常に一般的な誤解です。 数字のシーケンス内の依存関係を見つけるための特別な方法と手法があることに注意してください。
よく知られているテストの1つは、次のビットのテストです。これは、暗号強度について擬似乱数ジェネレーターをチェックするテストです。 このテストでは、ランダムシーケンスの最初のkビットを知っていれば、1/2よりも大きい確率でk + 1ビットを予測できる多項式アルゴリズムを使用しないでください。
暗号理論では、別の問題は、ジェネレーターによって生成された数字またはビットのシーケンスがどれくらいランダムであるかを決定することです。 通常、この目的のために、DIEHARDやNISTなどのさまざまな統計テストが使用されます。 1982年のAndrew Yaoは、「次のビットテスト」に合格したジェネレーターが、多項式時間で完了できる他のランダムランダム統計テストに合格することを証明しました。
インターネット
[10]で 、DIEHARDテストおよび他の多くのテストに合格して、アルゴリズムの重大な耐性を判断できます。
既知の乱数ジェネレーターのハッキング
参照資料
[1] Donald Knuth、プログラミングの技術(第2巻:派生アルゴリズム)
[2] Bruce Schneier、Applied Cryptography(第16章)
[4]
www.staff.uni-mainz.de/pommeren/Kryptologie/Bitstrom/2_Analyse/LCGcrack.html[5]
www.staff.uni-mainz.de/pommeren/Kryptologie99/English.html[6]
en.wikipedia.org/wiki/Mersenne_twister[7]
en.wikipedia.org/wiki/Triangular_distribution[8]
en.wikipedia.org/wiki/Linear_Congruent_Method[9]
zaic101.ru/files/728/using_linear_congruential_generators_for_cryptographic_purposes.pdf[10]
www.cacert.at/random[11]
www.cs.berkeley.edu/~daw/papers/ddj-netscape.html[12]
www.computerworld.com/s/article/9048438/Microsoft_confirms_that_XP_contains_random_number_generator_bug[13] md5
raz0r.name/articles/magiya-sluchajnyx-chisel-chast-2/comment-page-1を介した生成の興味深い例
が説明されていますオリジナル
jazzy.id.au/default/2010/09/20/cracking_random_number_generators_part_1.htmljazzy.id.au/default/2010/09/21/cracking_random_number_generators_part_2.htmljazzy.id.au/default/2010/09/22/cracking_random_number_generators_part_3.htmljazzy.id.au/default/2010/09/25/cracking_random_number_generators_part_4.html