プレフィックス検索ツリーのトピックは、ハブで何度も取り上げられています
ここでは、たとえば、プレフィックスツリーとは何か、なぜ必要なのかを簡単に説明し、そのようなツリーの基本的な操作(検索、挿入、削除)を説明します。 残念ながら、実装については何も言われていません。
この最近の投稿では、
libdatrieライブラリのCythonラッパーであるpython datrieライブラリを取り上げます。 最後のリンクでは、部分的に圧縮されたプレフィックスツリーの実装について、確定的な有限状態マシン(配列を使用)の形式で適切に説明しています。 ポインターを使用したプレフィックスツリーのC ++での実装を考慮して、このトピックに5セントを寄付することにしました。 さらに、バランスの取れたバイナリ検索ツリー(
AVLツリー )と圧縮されたプレフィックスツリーを使用して、文字列の検索を相互に比較するという別の目標がありました。
はじめに
プレフィックスツリーは、文字列などのビット構造を持つオブジェクトを格納するために設計されたデータ構造であることを思い出してください。 次に、ASCIIアルファベットの文字列を正確に格納するためのプレフィックスツリーの実装を検討します。各行は、文字列の他のどこにも見られない終端文字で終わります。 図と例では、終端記号はドル記号で示され、コードではヌル文字で示されます(したがって、実装では、文字列は標準C文字列であり、標準ライブラリstring.hを使用できます)。 他のアルファベットについては、次のすべてを基本的に継承する必要があります。
通常のプレフィックスツリーでは、特定のシンボルが各エッジに割り当てられ、頂点にはさまざまなサービス(またはユーザー)情報が格納されます。 したがって、ツリーのルートからリーフの一部へのパスは、正確に1行を定義します。 この文字列
は 、指定されたツリーに
格納されて
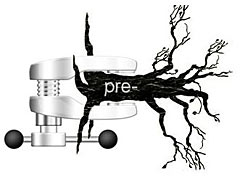
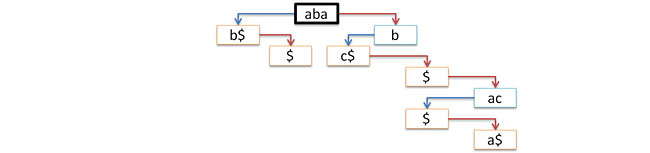
いると見なされます。 たとえば、次の図では、プレフィックスツリーには次の行セットが保存されています{abab $、aba $、bc $、b $、bac $、baca $}。 左側のルート、リーフ(それらの番号は行数と一致)-右側。 baca $行に対応するパスは赤で強調表示されます。
注意深い読者は、この実施形態では、プレフィックスツリーが通常の決定論的
有限状態機械であり 、その受け入れ状態がツリーの葉に対応することに気付くであろう。 実際、
libdatrieライブラリでのプレフィックスツリーの実装は、この考慮事項に
基づいています。 オートマトン自体は配列を使用して表されます。
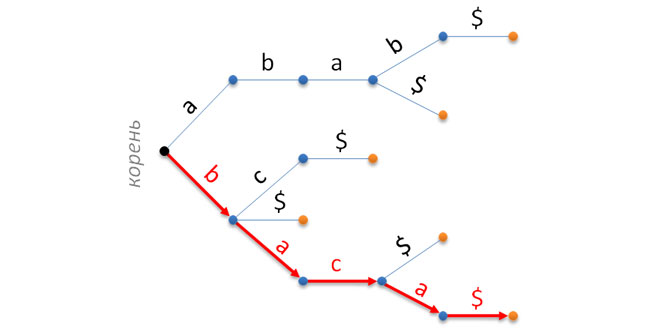
マシンのサイズを小さくするために、ツリーのすべての「テール」(葉を含む枝のないセクション)が行に詰められるとき、ツリーは部分的に圧縮された形式で使用されます(下図
a )。 さらに進んで、同様の方法で分岐せずにすべてのチェーンを圧縮できます(図
b )。 この場合、ツリーは有限状態マシンではなくなり(または、むしろ状態マシンのままですが、文字ではなく文字列のアルファベットより上にあります)、配列を使用した実装が問題になります-状態マシンと同様にツリーでの作業は、アルファベットのサイズが大きいという事実に大きく依存します有限であり、O(1)時間の任意の文字について、このアルファベットのシリアル番号を判別することができます(この手法は文字列では機能しません)。 ただし、ポインタが文字列ストレージの問題を実装している場合、それらは発生しません。

ポインターを使用したツリーの表現
したがって、ポインターによってツリーのエッジを表します。 まず第一に、この場合、情報を穏やかに置くためにツリーの端に情報を保存することはあまり便利ではないことに注意してください。 したがって、文字のチェーンをエッジから頂点に転送します(指向性ツリーの明らかなプロパティを使用して、ルートエッジを除くすべてのノードにエッジが正確に入ります)。 このような構造を取得します。
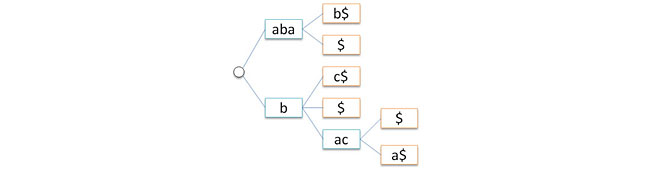
別の問題-ツリーノードの発信度は任意です(使用するアルファベットのサイズまで)。 この問題を解決するために、標準的な手法を適用します。つまり、各ノードに子ノードの
リストを保存します。 リストは単純に接続され、リストの先頭(長女)のみがノードに保存されます。 これにより、空のルートを同時に放棄できます。 これで、ツリーは古いルートの子ノードのリストの先頭へのポインターで表されます(つまり、ツリーをフォレストに置き換えます)。 したがって、各ノードには正確に2つのポインターが含まれるようになります。link-一番上の子ノードへ、次に-妹へ。 次の図は、このような変換のプロセスを示しています。青い矢印はリンクポインターに対応し、赤い矢印は次のポインターに対応します。
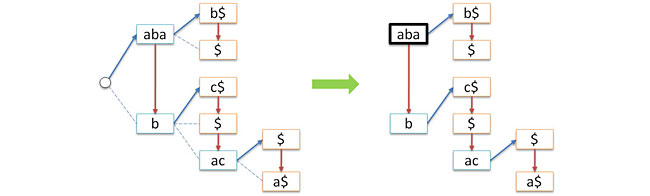
さらに、ツリーを操作するロジックを理解するには、左の図に示されている図を覚えておくと便利です。一方、ツリーの実際の表現は右の図のようになります。
そのため、気付かないうちに、可変の次数を持つツリー(一般ツリー)から、リンクおよび次のポインターが左右のサブツリーへのポインターの役割を果たす
バイナリツリーに切り替えました。 次の図はこれを示しています。
これで、実装に移ることができます。 ツリーノードはキーチェーンであり、その長さはlen(チェーンは終端文字で終わる必要はないため、その長さを明示的に知る必要があります)、および2つのリンクと次のポインター。 さらに、指定されたキーを持つ1つのノード(文字をコピーするために標準のstrncpy関数を使用)と、さらに最小のデストラクタで構成される単純なツリーを作成する最小コンストラクター。
struct node // { char* key; int len; node* link; node* next; node(char* x, int n) : len(n), link(0), next(0) { key = new char[n]; strncpy(key,x,n); } ~node() { delete[] key; } };
キー検索
最初に検討する操作は、プレフィックスツリーに新しい行を挿入する操作です。 検索のアイデアは標準です。 ツリーのルートから移動します。 ルートが空の場合、検索は失敗します。 それ以外の場合は、ノードのキーキーを現在の行xと比較します。 これを行うには、次の関数を使用します。この関数は、指定された長さの2行の最大共通プレフィックスの長さを計算します。
int prefix(char* x, int n, char* key, int m) // x key { for( int k=0; k<n; k++ ) if( k==m || x[k]!=key[k] ) return k; return n; }
検索の場合、次の3つのケースに関心があります。
- 一般的なプレフィックスは空にすることができます。次に、このノードの妹で再帰的に検索を続ける必要があります。 次のリンクをたどってください。
- 一般的なプレフィックスは検索文字列xと等しい-検索は成功し、ノードが見つかります(ここでは、終端記号の存在による文字列の終わりがツリーの葉でのみ見つかるという事実を本質的に使用します)。
- 一般的なプレフィックスはキーと一致しますが、xとは一致しません-シニア子ノードへのリンクリンクを再帰的に通過し、検索用に見つかったプレフィックスなしで文字列xを渡します。
共通の接頭辞はあるが、キーと一致しない場合、検索も失敗します。
node* find(node* t, char* x, int n=0) // x t { if( !n ) n = strlen(x)+1; if( !t ) return 0; int k = prefix(x,n,t->key,t->len); if( k==0 ) return find(t->next,x,n); // if( k==n ) return t; if( k==t->len ) return find(t->link,x+k,nk); // return 0; }
文字列xの長さnはデフォルトでゼロに等しい(そして明示的に計算される)ため、検索するツリーのルートと文字列のみを指定して検索関数を呼び出すことができます。
... node* p = find(t,"baca"); ...
次の図は、上のツリーで3行(1行は成功、2行はそうではない)を見つけるプロセスを示しています。

成功した場合、検索関数は検索が終了したツリーの葉へのポインタを返すことに注意してください。 目的の文字列に関連するすべての情報を見つける必要があるのは、このノードです。
キー挿入
(バイナリ検索ツリーのように)新しいキーを挿入することは、キーを見つけることに非常に似ています。 当然ながら、いくつかの違いがあります。 まず、空のツリーの場合、指定されたキーでノード(簡単なツリー)を作成し、このノードへのポインターを返す必要があります。 次に、現在のキーと現在の行xの共通プレフィックスの長さがゼロより大きく、キーの長さ(不適切な検索の2番目のケース)より小さい場合、現在のノードを2つに分割し、見つかったプレフィックスを親ノードに残し、残りのpを子ノードpに配置する必要がありますキーの一部。 この操作は、split関数によって実装されます。 分離後、見つかったプレフィックスなしでノードpに文字列xを挿入するプロセスを続行する必要があります。

ノード分割コード:
void split(node* t, int k) // t k- { node* p = new node(t->key+k,t->len-k); p->link = t->link; t->link = p; char* a = new char[k]; strncpy(a,t->key,k); delete[] t->key; t->key = a; t->len = k; }
コードを挿入:
node* insert(node* t, char* x, int n=0) // x t { if( !n ) n = strlen(x)+1; if( !t ) return new node(x,n); int k = prefix(x,n,t->key,t->len); if( k==0 ) t->next = insert(t->next,x,n); else if( k<n ) { if( k<t->len ) // ? split(t,k); t->link = insert(t->link,x+k,nk); } return t; }
キーabaca $およびabcd $を上記のツリーに挿入する例を次の図に示します。

指定された文字列xがすでにツリーに含まれている場合、挿入は行われないことに注意してください。 この観点から、プレフィックスツリーは立派なセットとして動作します。
キーの削除
通常、キーの削除は最も難しい操作です。 プレフィックスツリーの場合、すべてがそれほど怖くはありません。 実際には、キーが削除されると、削除されるキーのサフィックスに対応して、1つのリーフノードのみが削除されます。 最初にこのノードを見つけ、検索が成功した場合、それを削除し、このノードの妹へのポインターを返します(娘はありません、リストですが、姉妹は可能です)。

原則として、削除プロセスは完了している可能性がありますが、小さな問題が発生します。ノードを削除すると、2つのノードtとpのチェーンがツリー内に形成されます。 したがって、ツリーを圧縮形式で保持する場合は、これら2つのノードを1つに接続して、マージ操作を実行する必要があります。

マージ関数のコードは非常に簡単です。新しいキーを作成し、ノードpのサブツリーをノードtに再サスペンドし、ノードpを削除します。
void join(node* t) // t t->link { node* p = t->link; char* a = new char[t->len+p->len]; strncpy(a,t->key,t->len); strncpy(a+t->len,p->key,p->len); delete[] t->key; t->key = a; t->len += p->len; t->link = p->link; delete p; }
若いノードには親に関する情報がないため、シニアノードが合併の責任を負います。 合併の基準は、1)次ではなく、リンクによるキーの削除です。 2)削除後、新しいリンクには次のリンクがありません(子ノードが1つしかないため、現在のリンクとマージできます)。
node* remove(node* t, char* x, int n=0) // x t { if( !n ) n = strlen(x)+1; if( !t ) return 0; int k = prefix(x,n,t->key,t->len); if( k==n ) // { znode* p = t->next; delete t; return p; } if( k==0 ) t->next = remove(t->next, x, n); else if( k==t->len ) { t->link = remove(t->link, x+k, nk); if( t->link && !t->link->next ) // t ? join(t); } return t; }
マージせずにキーを削除する例:

そしてマージで:

有効性
動作時間とメモリ消費の観点から、AVLツリーとプレフィックスツリーを比較する小規模な数値研究が実施されました。 結果は、私にとってはやや落胆していることが判明しました(おそらく、誰かの手の湾曲が影響を受けたのでしょう)。 しかし、順番に...テストのために、8行のテストセットが形成されました。 それらの簡単な特性を表にリストします。

まず、指定された行のセットからツリーを構築するのに時間がかかり、同じセットからすべてのキーを検索するのに時間がかかりました(つまり、成功した検索のみ)。 次のグラフは、AVLツリーとプレフィックスツリーの構築時間の比較を示しています。 プレフィックスツリーが少し速く構築されていることがわかります。

次のグラフは、同じ2つのツリーで使用可能なすべてのキーを見つけるのにかかる時間の比較を示しています。 そして、ここではすべてが意図したものではないことが判明しました。 バランスの取れた二分木は、平均して接頭辞木の約半分の時間で検索します。

最後に、キャラクターごとのメモリコストがどのくらいかを見るのは興味深いものでした。 結果を次のグラフに示します。

平均して、両方のタイプのツリーで、文字ごとに約2バイトが取得されますが、これは私の意見ではそれほど悪くはありません。 興味深いことに、フラグの場合、プレフィックスツリーは1バイト未満の1文字(多くの一般的な長いプレフィックス)を消費します。
そのため、明確な勝者は結果として特定されませんでした。 行の数に対するこれら2つのツリーの動作時間を比較する必要がありますが、上記のグラフから判断すると、とにかく革新的なものは期待できません。 そしてもちろん、これら2つのアプローチをハッシュテーブルと比較することは興味深いでしょう...
ご清聴ありがとうございました!
コメントとコメントに感謝します!