透明度と表面の向き

先日、私の手でプラスチックカップを回すと、プラスチックの目に見える透明度は、表面を見る角度に依存することに気付きました-表面に垂直に見ると、背景がはっきりと見え、表面に沿って見ると、材料はほとんどなります不透明。 この現象に興味があり、数学モデルを作成することにしました。

すぐに言ってやった。 カットアウトの下に、数式出力、フラグメントシェーダーコード、および小さなデモがあります。

材料は光学的に均質であると仮定します-その光学特性は方向に依存しません。 次に、透明度の変化は、材料の厚さにおける光線の異なる経路長によって引き起こされます。



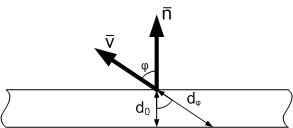
どこで 表面の単位法線ベクトル、 観測者への単位方向ベクトルです。

マテリアルの見かけの透明度は不透明度係数によって決定され、不透明度係数は次のようにマテリアルの色と背景色の混合を決定します。

どのように値を見てみましょう 材料の厚さに依存します。 これを行うには、厚さのある材料の層を破ります と不透明度 に 同じ厚さの層 それぞれに不透明度係数があります 。 させて -背景色 -材料の色、および -各レイヤーの出力の色。



しかしまた 、したがって：


つまり 厚さが増すと、材料の見かけの透明度は指数関数的に減少します。

厚さをしましょう その後：


したがって、目的の式：



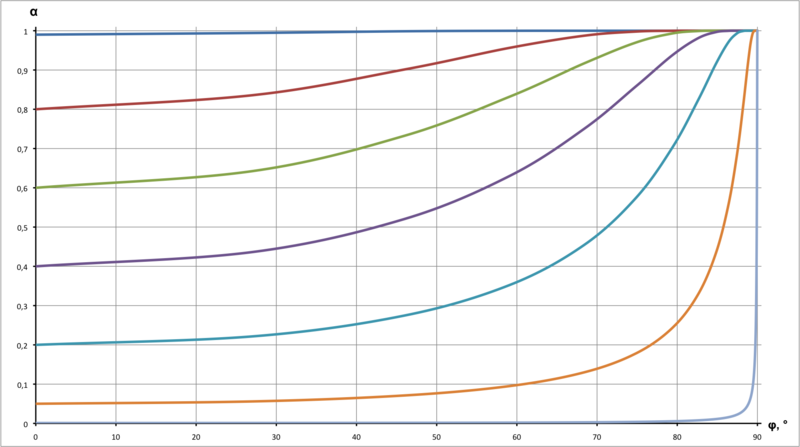
以下は、この数式を実装するフラグメントシェーダーのコードです。

varying vec4 v_color; varying vec3 v_normal; varying vec3 v_eye; void main(void) { //         float cosPhi = dot(v_normal, v_eye) / sqrt( dot(v_normal, v_normal) * dot(v_eye, v_eye) ); //    ,        //     ,      // 0.999 ^ 10000 = 4.5173346E-5 float alpha = 1.0 - pow(1.0 - v_color.a, 1.0 / max(abs(cosPhi), 0.00001)); gl_FragColor = vec4(vec3(v_color), alpha); }; 

結果は次のとおりです。


bitbucket.orgで入手可能なデモソースコード