1.基本
私たちのほとんどは数
独が何かを知っています。 ルールについては説明しませんが、すぐにテクニックに戻ります。
パズルを解決するために、複雑であろうと単純であろうと、塗りつぶしが明らかなセルが最初に検索されます。
1.1「最後のヒーロー」
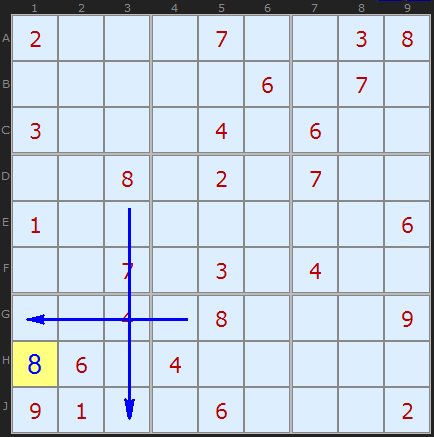
7番目の正方形を考えます。 空きセルは4つだけなので、すぐに何かを入力できます。
D3の 「
8 」は、
H3と
J3の充填をブロックします。 同様に、
G5の 「
8 」は
G1と
G2を閉じます
明確な良心をもって、
H1に 「
8 」を付けます
1.2行の「最後のヒーロー」
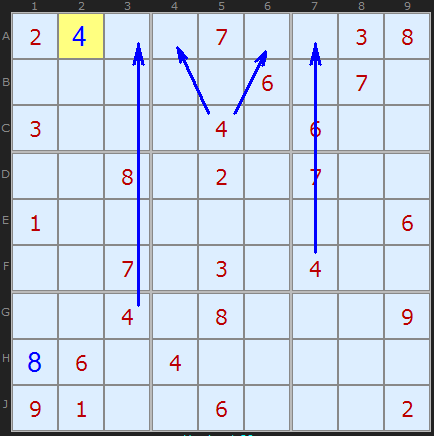
明らかな解決策を見つけるために四角を見た後、列と行に移動します。
フィールドで「
4 」を検討します。 彼女がライン
Aのどこかにいることは明らかです
。A3を開く
G3には「
4 」があり、
F7には
A7を削除する「
4 」があります。 また、2番目の正方形の別の「
4 」は、
A4と
A6での繰り返しを禁止しています。
「
4 」の「最後のヒーロー」は
A21.3「選択の余地はない」
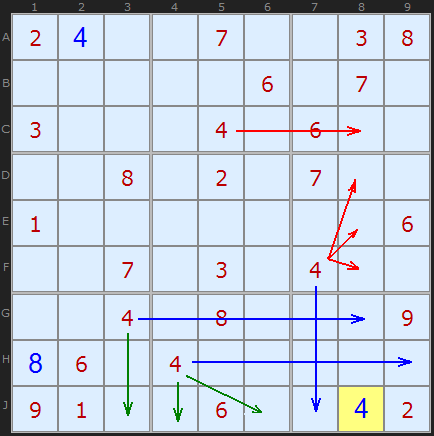
特定の場所にはいくつかの理由があります。
J8の 「
4 」は良い例です。
青い矢印は、これが最後の2乗可能な数であることを示しています。
赤と
青の矢印は、列
8の最後の数字を示しています。
緑の矢印は、行
Jの最後の可能な番号を示します
。ご覧のとおり、この "
4 "を代わりに配置する以外に選択肢はありません。
1.4「そして、もし私でないとしたら誰？」
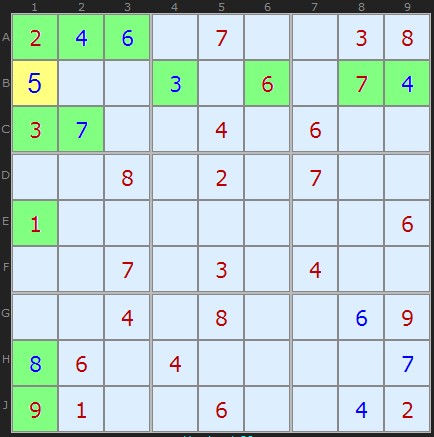
上記の方法を使用すると、数字を入力するのが簡単になります。 ただし、数値を最後の可能な値として確認すると、結果も得られます。 この方法は、すべての数値が存在するように見えても、何かが欠落している場合に使用する必要があります。
B1の 「
5 」は、「
5 」を除く「
1 」から「
9 」までのすべての数字が行、列、および正方形（緑色でマーク）にあるという事実に基づいて設定されます。
専門用語では、これは
Naked Aloneです。 フィールドに入力可能な値（候補）を入力すると、セルではそのような数値のみが使用可能になります。 この手法を開発すると、特定の行、列、または正方形に固有の「
隠しシングル 」を検索できます。
2.ザネイキッドマイル
2.1「裸の」カップル
「
ネイキッド」ペア 」
-1つの共通ブロックに属する2つのセルにある2つの候補のセット：行、列、正方形。
一般的なブロックから他のすべての候補を削除できる一方で、正しいパズルソリューションはこれらのセルとこれらの値のみに存在することは明らかです。
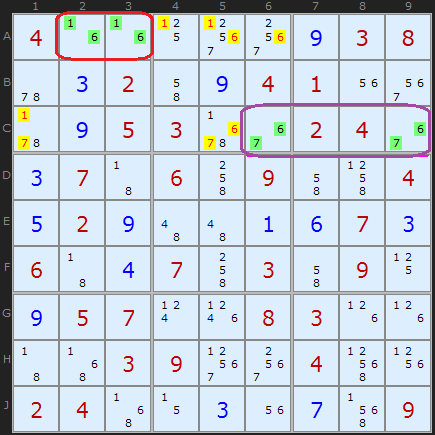
この例では、いくつかの「裸のペア」。
セル
A2と
A3は、行
Aで
赤で強調表示され、両方に「
1 」と「
6 」が含まれています。 ここにどのように配置されているのか正確にはわかりませんが、他のすべての「
1 」と「
6 」を行
A （黄色でマーク）から安全に削除できます。 また、
A2と
A3は共通の正方形に属しているため、
C1から「
1 」を削除します。
2.2「三人組」
The Naked Threeは、Naked Couplesの洗練されたバージョンです。
合計 3つの候補を含む1つのブロック内の3つのセルのグループは、
「裸の3」です。 そのようなグループが見つかった場合、これら3つの候補はブロック内の他のセルから削除できます。
「裸の3人」の候補の組み合わせは次のとおりです。
[abc] [abc] [abc] // 3つのセルに3つの数字。
[abc] [abc] [ab] //任意の組み合わせ。
[abc] [ab] [ab] //任意の組み合わせ。
[ab] [ac] [bc]
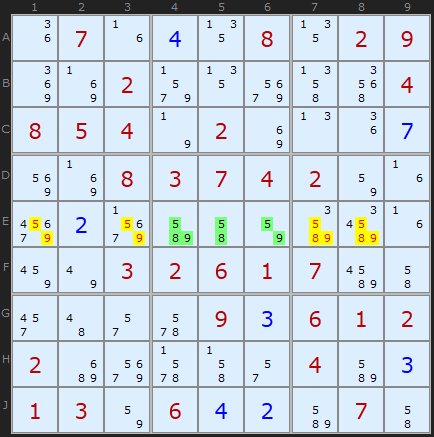
この例では、すべてが非常に明白です。 5番目の正方形では、セル
E4 、
E5 、
E6にはそれぞれ[
5,8,9 ]、[
5,8 ]、[
5,9 ]が含まれています。 一般に、これら3つのセルには[
5,8,9 ]があり、これらのセルのみがそこにあることが
わかります。 これにより、他のブロック候補からそれらを削除できます。 このトリックは、セル
E7の 「
3 」ソリューションを提供します。
2.3「壮大な4」
ネイキッドフォーは 、特に完全な形で非常にまれにしか発生しませんが、検出されると結果を出します。 決定のロジックは、
「ベアトリプル」のロジックと同じです。
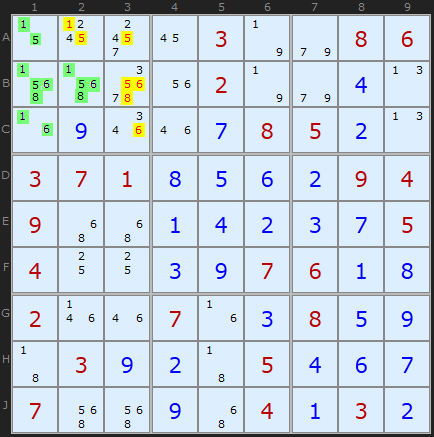
この例では、最初の正方形のセル
A1 、
B1 、
B2、および
C1には通常[
1,5,6,8 ]が含まれているため、これらの数値はこれらのセルのみを占有し、他のセルは占有しません。 黄色で強調表示された候補を削除します。
3.「すべての秘密が明らかになる」
3.1非表示のペア
フィールドを開く素晴らしい方法は、
隠されたペアを検索することです。 この方法を使用すると、セルから不要な候補を削除し、より興味深い戦略を開発できます。
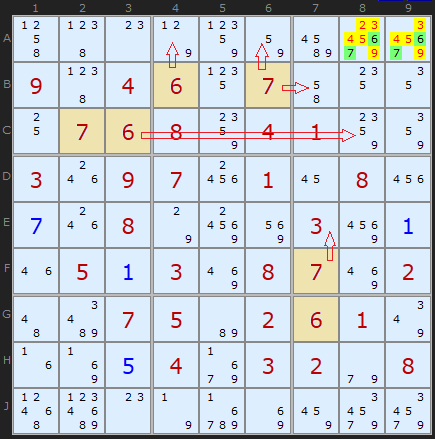
このパズルでは、
6と
7が1番目と2番目の正方形にあることがわかります。 さらに、
6と
7は列
7にあります。 これらの条件を組み合わせることにより、セル
A8と
A9にはこれらの値のみ
が存在し 、他のすべての候補が削除されると主張できます。
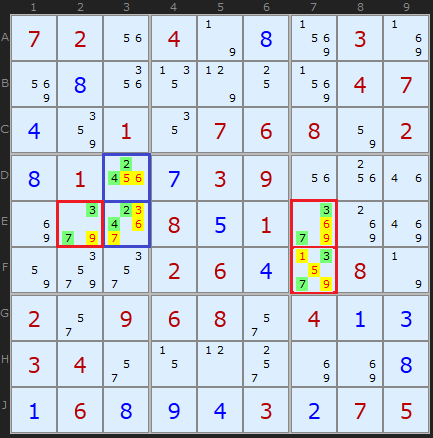隠されたペアのより興味深い、複雑な例。 青は
D3と
E3のペア[
2,4 ]で、これらのセルから
3、5、6、7を削除します。 [
3,7 ]で構成される2
つの隠されたペアは赤で強調表示されます。 一方では、列
7の 2つのセル、他方では行
Eで一意です
。 黄色で強調表示された候補は削除されます。
3.1非表示のトリプル
隠れペアから
隠れトリプル 、さらには
隠れフォーを開発できます。
隠されたトリプルは、1つのブロックにある3つの数字のペアで構成されます。 [a、b、c]、[a、b、c]、[a、b、c]など。 ただし、
「むき出しのトリプル」の場合のように、3つのセルのそれぞれに3つの番号を付ける必要はありません。 3つのセルの3つの数値
のみが機能します。 たとえば、[ab]、[ac]、[bc]。
非表示のトリプルはセル内の他の候補によってマスクされるため、まず
トリプルが特定のブロックに適用可能であることを確認する必要があります。
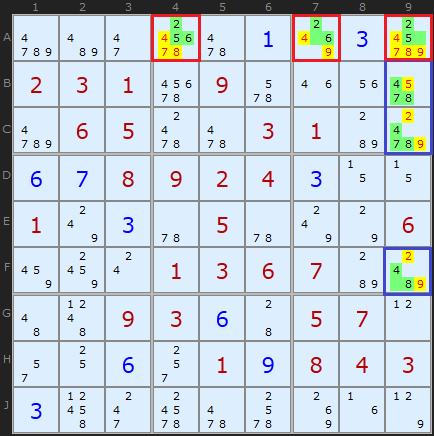
この複雑な例では、2つの
隠されたトリプルがあります。 赤でマークされた最初の列は列
Aにあります
。 セル
A4には、[
2,5,6 ]、
A7- [
2,6 ]、およびセル
A9- [
2,5 ]が含まれます。 これらの3つのセルは、2、5、または6が存在する可能性がある唯一のセルです。したがって、存在するのはそれらだけです。 したがって、不必要な候補を削除します。
2番目の列
9 。 [
4,7,8 ]は、セル
B9 、
C9 、および
F9に固有です。 同じロジックを使用して、候補を削除します。
3.1隠しフォー
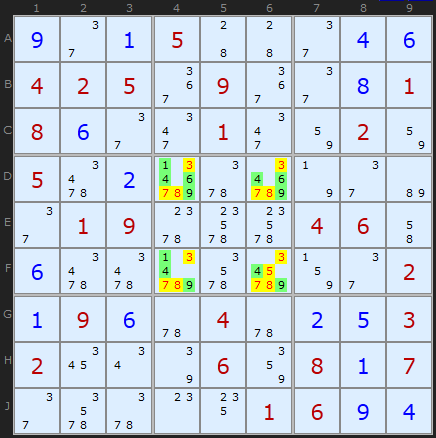隠されたフォースの素晴らしい例。 5番目の正方形の[
1,4,6,9 ]は、4つのセル
D4 、
D6 、
F4 、
F6にのみ存在できます。 ロジックに従って、他のすべての候補（黄色でマークされている）を削除します。
4.「ネレジノバヤ」
1つのブロック（行、列、正方形）に2つまたは3つの数字が表示される場合、共役ブロックからこの数字を削除できます。 ペアリングには4つのタイプがあります。
- ペアまたは3つの正方形-それらが同じ行にある場合、対応する行から他のすべての同じ値を削除できます。
- 正方形のペアまたはスリー-それらが1つの列にある場合、対応する列から他のすべての同じ値を削除できます。
- ペアまたは3行-それらが1つの正方形にある場合、対応する正方形から他のすべての同じ値を削除できます。
- 列のペアまたは3-それらが1つの正方形にある場合、対応する正方形から他のすべての同じ値を削除できます。
4.1ポインティングペア、トリプル
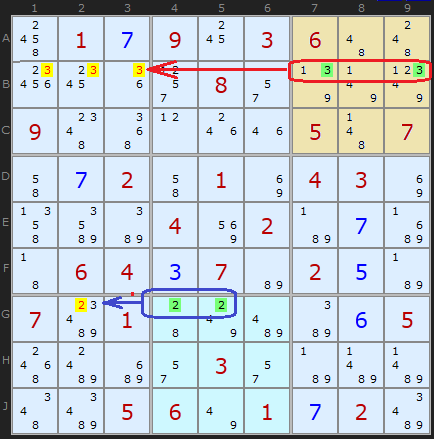
このパズルを例として示します。 3番目の正方形では、「
3 」は
B7と
B9でのみ見つかります。 ステートメント
1に続いて、
B1 、
B2 、
B3から候補を削除します。 同様に、8番目の正方形の「
2 」は
G2から可能な値を削除します。
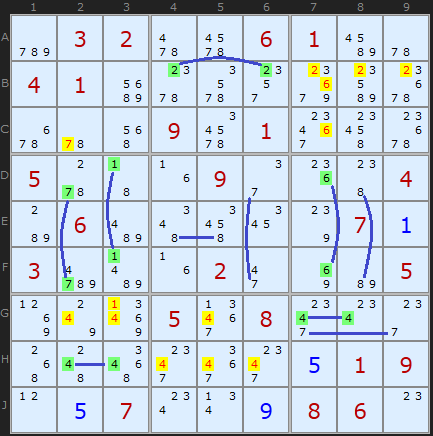
特別なパズル。 解決するのは非常に困難ですが、よく見ると、いくつかの
ポインティングペアに気付くでしょう。 ソリューションを進めるためにそれらをすべて見つける必要は必ずしもないことは明らかですが、そのようなそれぞれを見つけることで作業が容易になります。
4.2既約を減らす
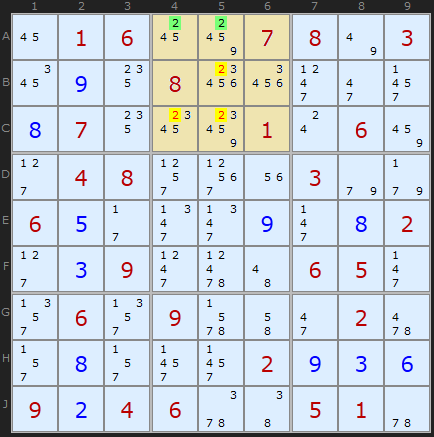
この戦略には、行と列と正方形の内容（ルール
No. 3 、
No。4 ）の正確な分析と比較が含まれます。
行
Aを検討します
。 「
2 」は
A4と
A5でのみ可能です。 ルール
3に従い、
B5 、
C4 、
C5の 「
2 」を削除します。
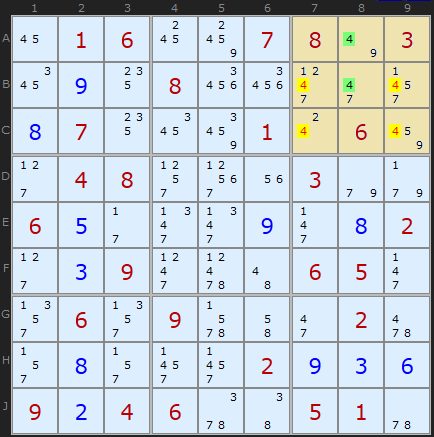
パズルを解決し続けます。
8列
目の 1つの正方形内に「
4 」の単一の配置があります。 ルール
No. 4に従って、不必要な候補を削除し、さらに
C7のソリューション "
2 "を取得します。
あとがき
数独を解くための数百の
アルゴリズムと
プログラムがあります。 時々、結果を得るために、単に
ウェブカメラを目指してください。 ただし、脳を鍛え、頭のアルゴリズムをスクロールするには、数独を解きながらペンと紙で座るのが便利です。
この記事では、基本的な決定アルゴリズムについて言及しました。 はい、はい、それは基本です。 次のステップは、高度で複雑な技術の分析です。 ご清聴ありがとうございました。