コンピューターポーカーの抽象化

まず、コンピューターポーカーは非常に重要なタスクです。なぜなら、ゲームの状態は膨大であり、このゲームに対する直接的な解決策を夢見る必要がないほど素晴らしいからです。 何らかの方法でポーカーのプレイ方法をマシンに教える唯一の方法は、抽象化に切り替えることです。これは、元のゲームの戦略的な状況が組み合わされたポーカーの小さなコピーです。 この記事が取り上げるのは、ポーカーの抽象化の問題です。

この出版物は、ある程度、 最初の部分に言及しており、読者がポーカーのルールに精通していることを前提としています。 私は一般的なスタイルのプレゼンテーションを厳守しようとします。詳細に興味がある人のために、コメントへの文献や議論へのリンクがあります。

なぜ抽象化が必要なのですか？

コンピューターポーカーの問題の規模を突き破るために、制限[および制限なし]の両方のポーカー分野のサイズを示すレポート[1]をよく理解することをお勧めします。 「最も単純な」制限のテキサスホールデムであっても、決定を下す必要があるゲームの状態は319,365,922,522,608だけです。 同時に、この種のポーカーでは6378種類の非ターミナルベットパターンしかなく、ゲームの状態のすべてはカードの組み合わせによって引き起こされます。 無制限のポットリミットの分野では、リミットリミットホールデムでは、10から^61の非ターミナル履歴のオーダーの500ブラインドのスタックで、数十のオーダーがリミットカウンターパートよりも多くベットします。 上記を読んだ後、読者はポーカーを直接表現で解決する現代のコンピューター技術の能力に疑問を抱くはずです。

元のゲームを単純化する方法は、このゲームの戦略的に近い状態を抽象化と呼ばれる新しいゲームの区別できない状態に結合します。 ポーカーには、抽象化に移行することで解決できる2つのクラスの問題があります。

• 無制限のポットリミットゲームでのベットの問題。
• 選手の手を表す問題。

抽象ゲームにおけるベットとその表現

ベットの問題は、特にポットリミットと無制限のポーカーの分野に関連していますが、多くのプレーヤーがいるリミットゲームでは、ベットパターンの数を減らす必要がある場合があります。 ここで最も人気のあるトリックの1つは、賭けの範囲を間隔に分割し、すべての操作が範囲に結び付けられた賭けで実行される場合の、賭けの離散化です 。

無制限のポーカーの離散化オプションについて考えてみましょう。料金は次のように定義されています。h-銀行の半分、 p-銀行への料金、 d-銀行の2倍、 a-オールイン。 他のすべてのベットは、上記の最も近いものに関連します。 一見したところ、このようなベットの抽象化は非常に適切であり、実際、それを使用するボットは同じベット方式を遵守する対戦相手との良好なレベルのプレイを実証します（例えば、[2]を参照）。 しかし、敵が突然個別の賭けとは非常に異なる任意の賭けをした場合、ボットの不適切な動作が保証されます。 最も明らかな潜在的な脆弱性は、ボットが単純にフォールドすることができる最小の許容可能な賭けをする相手です。 さらに、離散範囲間の境界でのレートは、ボットによる「過大評価」または「過小評価」の決定の採用につながります。これは、遠くでお金を失い、人がボットを開くことに満ちています。 個別の範囲を追加しても状況は保存されません。抽象的なゲームの状態の数が増え、カードの抽象的な表現の品質を低下させる必要があるためです。

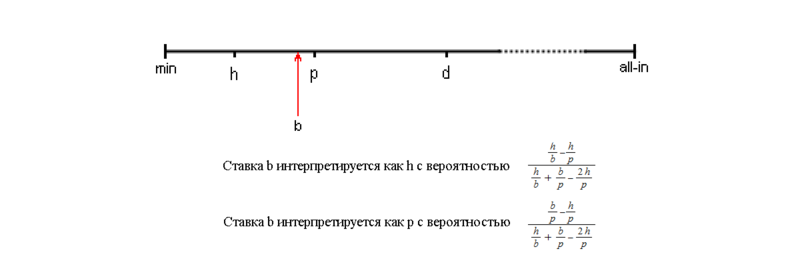「ハード」ブロードキャストの場合は抽象レートp、または「ソフト」放送の抽象レートhおよびpのいずれかへの実レートbの離散化。

実際のゲームの賭けを抽象的なものに変換するための上記のスキームは、「タフ」と呼ばれます。 ベットをブロードキャストする別の「ソフト」方法があります。その本質は、実際のベットと特定のアブストラクトとの相関がランダムに決定され、実際のベットがアブストラクトに近いほど、相関の可能性が高くなります。 プレゼンテーション[3]には、「ソフト」なブロードキャスト方法により、ボットが賭けの大きさによって悪用されることは少なくなりますが、同時に収益性が低下するという情報が含まれています。

人々と遊ぶことに焦点を当てたポーカーエージェントを構築する場合、多くの場合、実際のゲーム分布を分析することでベットの離散化が行われ、その後、各ゲーム状態に独自のベット離散化スキームが割り当てられます。 ただし、抽象化を構築するためのスキームを特定した後、このアプローチは依然として脆弱です。 離散化はポーカーベットを表す唯一の方法ではありません。 アプローチも可能です。これは、ポーカーエージェントが、抽象化に含まれる値に合わせて銀行を厳密に定義された金額で補おうとするという事実から成ります。 明らかに、このようなトリックはすぐにボットを公開し、同時に重大な欠陥がないわけではありません。たとえば、銀行の固定サイズをわずかに超えることで、ボットにカードを強制的に破棄させることができます。

最近、ポーカーの賭けの抽象化を構築する方法が開発されました。この方法では、別のゲームエージェントが導入され、特定のゲーム状況でどの賭けを行うべきかを決定します。 [4-5]では、各ゲーム状態で可能なすべての賭けの代わりに、プレーヤーは最小賭け（L）、最大賭け（H）、またはオールインの3つだけを行うことができます。 この場合、2つの賭けLまたはHのどちらを行う必要があるかの決定は、新しいゲーミングエージェントが行います。 このアプローチの明らかな利点は、ベットサイズでボットを悪用することの難しさですが、同時に、新しく導入されたエージェントのトレーニング、LレートとHレートの特定の値の発見、および全体としての抽象化のプレゼンテーションの編成に関連する質問が発生します。


無制限のポーカーでベットを提示するさまざまな方法。


時には、トレーディングサークルへのベット数が制限されているか、以前のサークルの履歴が完全に存在しないという抽象化があります。 しかし、今日、そのようなアプローチは弱いポーカーエージェントを生成するため、特に人気がありません。

抽象化におけるマップの組み合わせ

ポーカーの抽象化を構築する上で最も困難で最も重要なことは、カードの組み合わせの提示です。 これが、ボットが現在のゲーム状況をどの程度適切に認識し、戦略的に正しい決定を下すかを決定するものです。

以下はレポート[1]の表で、各ラウンドのテキサスホールデムのすべての種類のカードの組み合わせのセットのサイズを示しています。 最初の列は、ボード上の一般的なカードと組み合わせてポケットカードを両方のプレーヤーに配布するためのオプションを示しています。 2番目の列には同じ情報が含まれていますが、1人のプレーヤー、つまり 1組のポケットカードとコミュニティカードの組み合わせ。 最後に、最後の列には、1人のプレーヤーのカードの組み合わせの同等でないクラスの数が含まれています。 同等の組み合わせは、スーツを変更することで同じセットから他の組み合わせを取得できるカードの組み合わせのセットであることを思い出してください。 同等の組み合わせに同じ戦略情報が含まれていることは明らかです。

貿易の輪	ちょうど二人用	1人のプレーヤーの合計	シングルプレイヤーでは非同等
プリフロップ	1,624,350	1,326	169
フロップ	28,094,757,600	25,989,600	1,286,792
回す	1,264,264,092,000	1,221,511,200	55,190,538
川	55,627,620,048,000	56,189,515,200	2,428,287,420

同等のクラスの例は、3回目のベッティングラウンドでのAKx|TxJy82xの組み合わせAKx|TxJy82x AKxはプレーヤーのポケットカード、 TxJy82xはボード上のカードの出現順、 xとy （ x!=y 、もちろん）は4つのうちの1つですスーツ{c,s,h,d} 。 したがって、クラスAKx|TxJy82xは、まったく同じ12個の組み合わせ{AKc|TcJs82c, AKs|TsJc82s, ...}ます。 AKx|TxJy82xの形式で記述された組み合わせをプレーヤーの手と呼ぶことに同意しましょう。ただし、これAKx|TxJy82x 一般に受け入れられている定義と多少AKx|TxJy82x ます 。 それでも、「ハンド」という用語は、1人のプレーヤーだけが完全にアクセスできるプライベートカード情報の定義に完全に適合しています。

同等のクラスに手を加えた後でも、直接検討するにはあまりにも多くの人がいるため、これらの同等のクラスを新しい抽象クラスにグループ化することに頼る必要があります。 もちろん、現在、この手順は、元の同等のクラスに関する情報の一部が失われた状態で発生します。

このようなハンドのグループ化の例については、プリフロップを考えてください。これには、等価でないポケットペアが169個しかないためです。 興味のある多くの読者は、有名な理論家でありポーカープレーヤーであるDavid Sklanskyの名前をよく知っています。その成果の1つは、プリフロップでのプレーに関する詳細な戦略です。 以下の図は、Sklansky [6]によって提案された戦略的価値に応じたスターティングハンドのグループ化を示しています。 この8つのクラスへの分割は真の1つだけではありませんが、ポーカーでカードの抽象化を構築する原則についての良いアイデアを提供します。



残念ながら、フロップから始めて、カードの組み合わせの手動分析は非常に退屈で感謝のない作業であるため、手を分析してクラスに分類する他の方法に頼らなければなりません。 選択したプロパティに従ってカードの組み合わせをグループ化できる、カードの組み合わせの数値特性について説明します。

使用された最初の特性の1つはハンドのランク （Hand Strength、 HS ）でした。これは、プレーヤーの完成したコンビネーションよりも劣る、対戦相手のすべての可能なコンビネーションの割合として定義されます。 たとえば、既製のシニアフラッシュがあるためHS(AKx|TxJy82x)=1.0ですが、 HS(AxKy|TzJx82z)~0.43は驚くことではありません。

HS分析する際に最初に目を引くのは、このインジケーターが後続のラウンドでのプレイヤーのハンドの振る舞いについて何も言っていないことです。もちろん、分布履歴はこのインジケーターの値に影響を与えません。 フロップから始めて、不足している情報を埋めるために、 NPot （Positive Potential）とNPot （Negative Potential）の2つのNPotが導入されます。 これらのPPotインジケーターの最初は、新しいカードがテーブルに表示された後、プレーヤーの現在のハンドが向上する確率です。 改善とは、対戦相手がプレーヤーの完成した組み合わせよりも古い既製の新しい組み合わせを持たないことを意味します。 同様に、 Npotは、テーブルに新しいカードをNpotとプレーヤーの手が悪化する確率です。 これらの指標の詳細な説明とその計算手順は、[7-8]に記載されています。 上記の例では、 PPot(AKx|TxJy82x)=0およびNPot(AKx|TxJy82x)~0これは、対戦相手が2組の準備ができている場合にフルハウスのみに依存するため、驚くことではありません。 2番目のケースでは、 PPot(AxKy|TzJx82z)~0.15およびNPot(AxKy|TzJx82z)~0.22 NPotあり、フラッシュを収集するために相手がスーツxで行方不明のカードを拾うことができるという事実により、 NPot非常に高いことがNPotます。

[9]では、予想されるハンドランクE[HS ² ] ²乗により、より優れた抽象化が得られるという情報が提示されます。このインジケーターは、プレーヤーの強いハンドにより多くの利点を与え、ポテンシャルの高いハンド（ PPot ）で区切るからです。 ランクは同じですが、ポテンシャルが異なるハンドは、異なる方法で戦略的にプレーする必要があるため、論理的です。

3つのインジケータ{HS, PPot, NPot}使用すると、プレーヤーのハンドをより正確に特徴付けることができますが、同時に考慮することは多少不快になる可能性があるため、多くの場合、2つの式[7 -8]： EHS ₁ = HS×(1−NPot)+(1−HS)×PPot 、またはEHS ₂ = HS+(1−HS)×PPot 。 2つの式の違いは、 EHS ₂ EHS 「楽観的な」予測を提供することです。これは、より攻撃的なゲームを作成するために必要です。

多くの人がすでに推測しているもう1つの指標は、ショーダウンでのハンドの勝率または予想されるランクです （予想されるハンドの強さ、 E[HS] ）。 この特性の名前が明確に示すように、これは、ショーダウンの前にプレーを終えた現在のプレーヤーが、相手の可能な組み合わせよりも古い組み合わせを獲得するケースの割合を表します。 この指標の利点は、 NPotやNPotとは対照的に、ショーダウンまでの後続のすべてのトレーディングサークルのハンドのダイナミクスに関する情報がすでに含まれていることです。 上記の例では、相手のランダムハンドに対して、これらのインジケーターの値はE[HS](AKx|TxJy82x)~0.99およびE[HS](AxKy|TzJx82z)~0.42です。

上記のすべての指標には、多くの一般的な欠点があります。 そのうちの1つは、経験豊富なポーカープレーヤーにとって最も注目すべきことです。これらのインジケーターは、対戦相手がハンドを持っているという仮定に基づいて計算されます。 ポイントは、ポーカーでは非常に少ない割合のハンドがショーダウンすることです。つまり、 HS 、 NPot 、 NPotまたはE[HS]を計算するときに、相手が持っていない可能性のあるすべてのポケットカードを置きます。 これにより、このような指標の予測が予想外に高くなります。 この欠点を何らかの形で修正するために、多くの場合、ゲームの状況に応じて対戦相手に可能な手の重み付けを使用します。 特に、そのような重み付けは、相手をモデル化することで実行できます。

2番目の欠点は、これらのインジケーターを使用してもプレーヤーの手に関する情報が失われることですが、これはそれほど明白ではありません。 まず第一に、それは手の「記憶」、すなわち、ボード上でカードが出現した順番に関する情報に関係します。 たとえば、 HS(AKx|QJT5x)=HS(AKx|JT5Qx)であることが明らかです。最初のケースでは、フロップのプレーヤーはすでに既製のストレートフラッシュコンビネーションを持っていました。 さらに、多くの場合、異なる戦略的決定を必要とするハンドは、互いに近い数値インジケーターの値を持っているため、ポーカーのプレイ方法を機械に教える際にエラーにつながる可能性があります。

抽象化を構築するための数値インジケータをさらに操作すると、これらのインジケータの特定の値に応じて、さまざまな手のカテゴリをクラスにグループ化することになります。 たとえば、ベットの各ラウンドで5つのクラスのみを持ちたい場合、以下のE[HS]値に従ってすべてのハンドをグループ化できます。
[0.0–0.2] [0.2–0.4] [0.4–0.6] [0.6–0.8] [0.8–1.0]
現在、抽象的なポーカーゲームは、元のカードの組み合わせではなく、5つの手のクラスによって操作されます。 このような抽象的なゲームを完成させるには、トレーディングサークルの変化におけるクラス間の遷移の確率を計算し、ある抽象的な手のクラスの「収益性」を示すペイアウトマトリックスを指定する必要もあります。

手をクラスにグループ化することによる抽象化は、手動または自動化された手順（データクラスタリング手法など）を使用して実行できます。 抽象化を手動で作成すると、ボットの決定をある程度理解できるようになり、デバッグと戦略の調整が容易になりますが、非常に時間がかかるプロセスです。 多くの場合、自動グループ化方法は、ポーカーのタスクに必ずしも当てはまらない基準に基づいています。 一方、自動アプローチでは、抽象化のパラメータを簡単かつ迅速に操作できるため、適切な構成を迅速かつ最適に選択できます。

E[HS]値の事前に定義された5つの間隔を使用して手をクラスに分割する上記の例には、1つの欠点があります-クラス間で不均等に分布します-いくつかの手のみがE[HS]値のある範囲に入り、残りは過密になります。 この状況を修正するには、クラスの手動編集、変位値の計算、ネストされたクラス、k-meansなどへの分割など、さまざまなトリックを使用します。


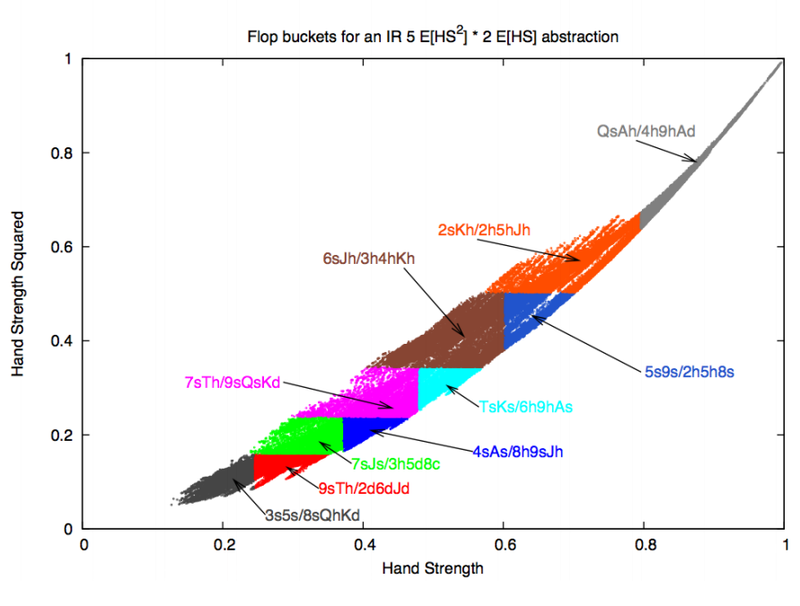入れ子クラスに分割されたフロップでインジケーターE[HS ² ]およびE[HS]を使用してハンドをグループ化する例。

おわりに

私の謙虚な意見では、現代のコンピューターポーカーは抽象化のゲームであり、抽象化がより良く、より正確で、重要なことに、より少ないことが判明したエージェントが勝ちます。 抽象化のサイズは無駄に言及されていません。なぜなら、ゲームのエージェントのトレーニングに費やされる時間が依存するからです。 そして、それが数千年、数年、または数時間になるかどうかは、抽象化の構造を設計する研究者に依存します。 残念ながら、この出版物は抽象化を構築するためのさまざまなアプローチの完全な概要であると決して主張することはできません。 それでも、この分野の主要なポイントは反映されており、コンピューターポーカーの問題について読者に興味を持たせるという目標は達成されたと思います。