Wolfram Mathematicaのさまざまな方法を使用して、道路上のカメラの設置角度を見つける問題を解決します。 パート2

前回、ファイルからデータをダウンロードし、構造に分類し、車両の軌道の方程式を取得して、このデータをグラフィカルに表示しました： パート1

この記事では、方法の1つは、車両の動きのトラックが交差する付近で統計的にポイントを見つけることです。

興味のあるポイントを見つける方法の1つの説明

この方法では、グラフのすべての交点、つまり車両の動きの軌跡を見つけ、このデータの数学的期待値と分散を見つけます。

すべてのトラックの交点を見つける

方程式のリストで方程式の数を定義します。

length = Length[numeq];

トラックの交差点の座標を記録する空のリストを作成します。

rootlist = {};

ここで、ループを作成する必要があります。 ペアになっている線形方程式を解き、それらの交点の座標を見つけて準備リストに書き込みます。

Do[Do[rootlist = Append[rootlist, List[
x /. Solve[numeq[[j]] == numeq[[i]], x][[1]],
numeq[[j]] /. Solve[numeq[[j]] == numeq[[i]], x][[1]]
]
]
, {i, 1 + j, length}],
{j, 1, length}]

サイクルの各パスで、 jおよびi方程式の交点のxおよびy座標で構成されるリストをrootlistリストに追加しますrootlist座標は次のようになります。

x /. Solve[numeq[[j]] == numeq[[i]], x][[1]]

しながら

Solve[numeq[[j]] == numeq[[i]], x]

この方程式の根のリストを返します。

{{x -> 2586.14}}

、そして私たちのレコードは最初のルートを選択します、それはここで唯一のものであり、置換を実行します。 /.演算子の前のxの代わりに/. その値x -> 2586.14ます。

expr /. x > value expr /. x > value -expr式で、変数xの代わりに、
値値。

したがって、2つのトラックの交差点の座標Xが見つかり、同様のアクションが座標Yを見つけるために行われ、ルート値のみが方程式の1つ、この場合はインデックスjに代入され、これはインデックスiの方程式でもあります：

numeq[[j]] /. Solve[numeq[[j]] == numeq[[i]], x][[1]]

次に、ポイントの値を全体に四捨五入します。

rootlist = Round[rootlist];

これで、トラックの交点のリストが作成され、統計処理を開始できます。

リストは次のようになります。

{{2586, -910}, {2716, -1014}, {2718, -1015}, {3566, -1697}, {2697, -999}, {2957, -1207}, ... }

結果の統計処理

交差リストのX座標のマット期待値を定義します。

Xmed = Mean[rootlist[[All, 1]]] // N
2532.7

Mean[data] -データdataの平均値を返します。

N[expr, n] -式exprを小数点以下n桁以内に評価した結果を返します

x // f - f[x]接尾辞形式

交差リストのX座標の分散を定義します。

sX = StandardDeviation[rootlist[[All, 1]]] // N
81038.5

StandardDeviation[data] -ロシア語で言えば、データの標準偏差を返します-関数はシグマ、ウェル、または標準偏差を返します。

交差点のY座標に対して同じ特性を定義します。

Ymed = Mean[rootlist[[All, 2]]] // N
sY = StandardDeviation[rootlist[[All, 2]]] // N
-699.907
106488

得られた数学的期待値のデータから、望ましい値、つまり縁石の縁に対するカメラの回転角度を決定することがすでに可能です。

Xangle = Xang Xmed/Xlen - Xang/2 // N
8.02449

、および車両経路に対するカムコーダーの角度

Yangle = Abs[Yang Ymed/Ylen - Yang/2] // N
9.38796

一般に、標準偏差のこのような大きな値はやや混乱を招きます。 ヒストグラムを作成して数量の分布を確認し、これが発生する理由を見つけます。

Histogram[
{rootlist[[Range[length], 1]],
rootlist[[Range[length], 2]]},
100, AspectRatio -> 1]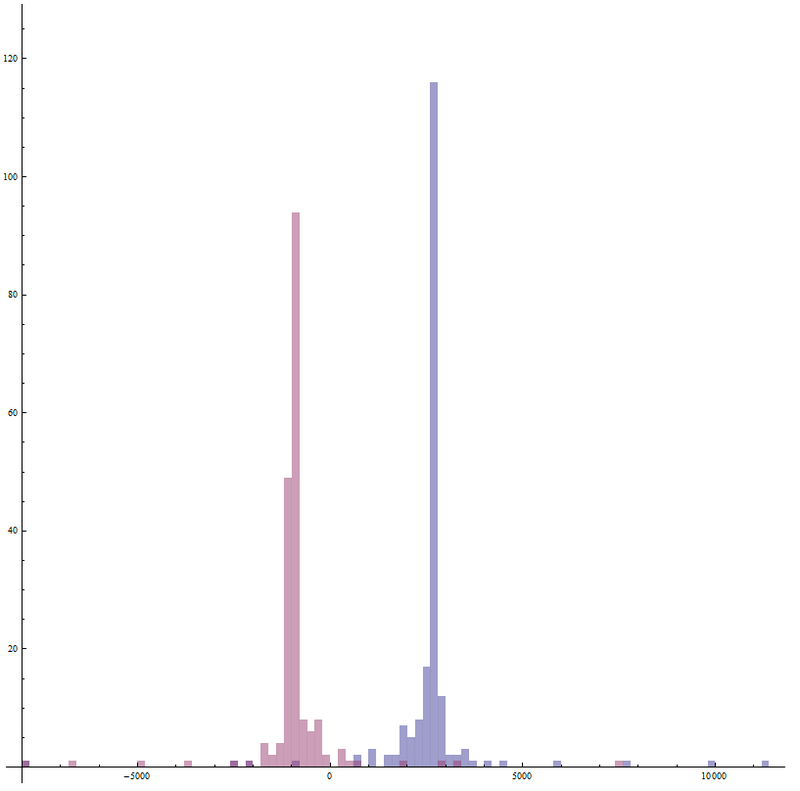


Histogram[list,bspec] bspec列の数でリストlistヒストグラムをbspecます

このヒストグラムから、大きさの数学的期待からはほど遠い交点があることがわかります。

次の条件を満たさないポイントを考慮に入れないようにしましょう。

ポイントのX座標は、[-カメラの水平解像度; 2つの水平カメラ解像度]
ポイントのY座標は、カメラの垂直解像度の[-2以内でなければなりません。 0.5カメラ解像度垂直]

これを行うには、次のように記述します。

length = Length[rootlist];
rlist = {};
Do[If[
-Xlen < rootlist[[i, 1]] < 2 Xlen && -2 Ylen < rootlist[[i, 2]] < 0.5 Ylen,
rlist = Append[rlist, rootlist[[i]]]]
, {i, length}]

If[condition, t, f] - conditionの評価結果がTrue場合t返し、結果がFalse場合f返します

And[p,q,...]またはp && q && ...論理加算-操作 "And";

結果のフィルター処理されたサンプルの期待値と標準偏差を評価します。

Xmed = Mean[rlist[[Range[length], 1]]] // N
Ymed = Mean[rlist[[Range[length], 2]]] // N
sX = StandardDeviation[rlist[[Range[length], 1]]] // N
sY = StandardDeviation[rlist[[Range[length], 2]]] // N
2628.84
-928.819
353.112
457.717

結果のフィルター処理されたサンプルの散布は、完全なサンプルの散布よりも小さくなります。 希望の角度は、サンプル全体の場合と同じ方法で決定できます。

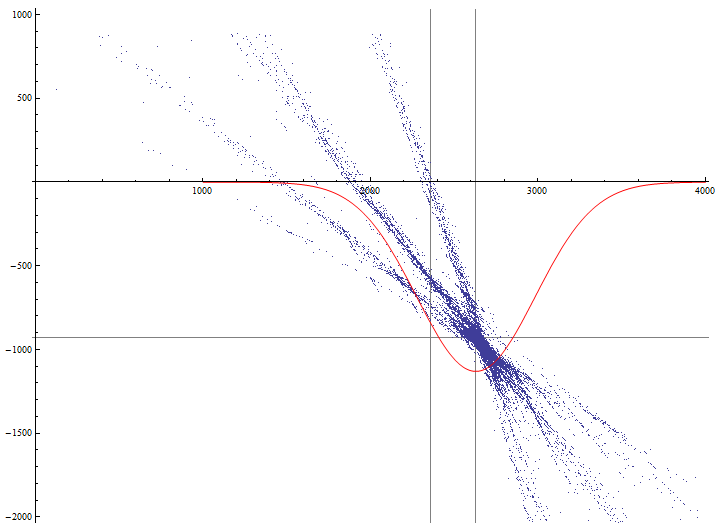
結果のグラフィック表示。

次に、フィルター処理されたサンプルの交点と交点のX座標の分布関数を1つのグラフに表示します。

lp = ListPlot[rlist, PlotStyle -> PointSize[0.0005], GridLines -> {{Xlen, Xmed}, {Ylen, Ymed}}, AspectRatio -> Automatic];
dp = Plot[-1000000 PDF[NormalDistribution[Xmed, sX], x], {x,1000, 4000}, PlotStyle -> {Red}];
Show[lp, dp, PlotRange -> {{0, 4000}, {-2000, 1000}}, AxesOrigin -> {0, 0}]



PDF[dist,x] -引数xと指定された分布則dist持つ分布の確率密度の値を返します

NormalDistribution[mu,sigma] -正規分布

少しだまして、グラフを明確にするために係数-1000000を設定しました。

次は？

次の記事では、フィルタリング式とセット内のサブセットの検索に基づいて、交点を決定する別の方法を示します。