このブログでは、主な推奨アルゴリズムの簡単な説明(
タスク設定 、
ユーザーベースおよびアイテムベース 、SVD:
1、2、3、4 )、コンテンツを操作するためのいくつかのモデル(
naive Bayes 、
LDA 、
テキスト分析方法のレビュー )、コールドスタートに関する一連の記事(
タスク設定 、
テキストマイニング 、
タグ )、多腕バンディットに関するミニシリーズ(
パート1 、
パート2 )がありました。
これらのメソッドや他の多くのメソッドを共通のコンテキストに進めていくには、共通のベースを開発し、現代のデータ処理メソッドが話す言語、つまり
グラフィカルな確率モデルの言語を学ぶ必要があり
ます 。 今日は、この物語の最初の部分であり、最も単純で、写真と説明があります。

ベイジアン推論問題
最初に、
すでに話したことを簡単に思い出し
てください 。 機械学習の主なツールはベイズの定理です。
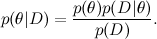
ここで、Dはデータ、私たちが知っていること、θはトレーニングしたいモデルパラメーターです。 たとえば
、SVDモデルでは、データはユーザーが製品に付けた評価であり、モデルパラメーターはユーザーと製品に対してトレーニングする要因です。
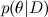
-これは、データを考慮した
後のモデルパラメーターの確率分布である、見つけたいものです。 これは
事後確率と呼ばれます。 原則として、この確率は直接見つけることができず、ここではベイズの定理が必要です。
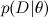
-これは、いわゆる
尤度 (尤度)であり、モデルパラメーターが固定されている場合のデータの確率です。 これは通常、簡単に見つけることができます。実際、モデルの設計は通常、尤度関数を設定することにあります。 A
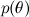
-事前確率、オブジェクトに関する直感の数学的形式化、実験前であっても以前に知っていたことの形式化。
したがって、ベイジアン結論の主なタスクの1つに到達します。仮説/パラメーターの事後分布を見つけるには:
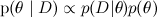
最大事後仮説を見つける
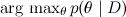
。
複雑な分布とベイジアンネットワークの因数分解
しかし、すべてが非常に単純な場合-2つの関数を乗算し、結果を最大化した-科学全体は何ですか? 問題は、関心のある分布が通常複雑すぎて、分析的に直接最大化できないことです。 それらの変数が多すぎる;変数間の関係が複雑すぎる。 しかし、一方で、多くの場合、使用できる追加の構造、
独立の形式の構造(
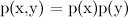
)および
条件付き独立 (
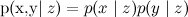
)いくつかの変数。
素朴なベイズに関する会話を思い出して
ください。モデルでは、圧倒的な数のパラメーターがあることが判明しました。また、次のトピックを条件に、属性(単語)の条件付き独立性について追加の仮定を立てました。
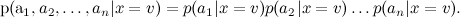
結果は複雑な事後分布です
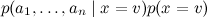
なんとか書き直した
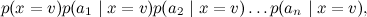
この形式では、対処がはるかに簡単であることが判明しました(各小さな分布のパラメーターを個別に学習し、製品の最大値を与える
vを選択します)。 これは、複雑な分布を単純な分布に分解(分解)する最も単純な例の1つです。 今日および以降のテキストでは、この方法を一般化し、他の追随を許さない高さにすることができます。
したがって、大きく複雑な確率分布を表す最も便利な方法の1つであるベイズの信念ネットワークを見てみましょう。最近ではしばしば単純なグラフィカルモデルと呼ばれています。 ベイジアンネットワークは、有向サイクルのない有向グラフです(これは非常に重要な条件です!)頂点は分布の変数に対応し、エッジは「接続された」変数を接続します。 各ノードでは、ノードの条件付き分布が指定されますが、その親は
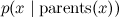
、およびベイジアンネットワークのグラフは、大きな結合分布がこれらの条件付き分布の積に分解されることを意味します。
たとえば、単純なベイズに対応するグラフは次のとおりです。
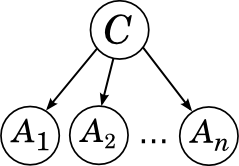
分解に対応
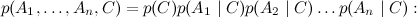 Cには
Cには祖先
がないため、無条件(限界)分布を使用し、各
A iは
Cから直接「成長」し、他の誰とも接続されていません。
この場合、すべての属性
A iがカテゴリ
Cの条件の下で条件付きで独立していることがすでにわかっています。
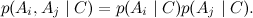
ここで、最も単純なすべてのベイジアンネットワークバリアントを検討し、それらが対応する変数間の独立条件を確認してみましょう。
2つおよび3つの変数を持つベイジアンネットワーク:些細なケース
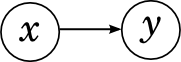
2つの変数
xと
yのネットワークから始めます。 オプションは2つしかありません
。xと
yの間にエッジがないか、またはあります。 エッジがない場合、それは単に
xと
yが独立していることを意味します。そのようなグラフは展開に対応するからです
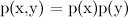
。

そして、エッジがある場合(
xから
yに進み、それは重要ではありません)、分解を取得します
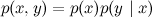
、どの分布に対しても、条件付き確率の定義により、文字通り常にばかげている
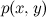
。 したがって、エッジを持つ2つの頂点のグラフでは、新しい情報は得られません。
次に、3つの変数
x 、
y 、および
zのネットワークに移動します。 最も単純なケースは、エッジがまったくない場合です。
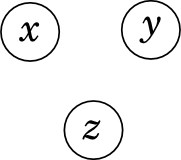
2つの変数と同様に、これは
x 、
y 、および
zが単純に独立して
いることを意味します。
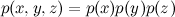
。
別の単純なケースは、変数間に
すべてのエッジが描画される場合です。
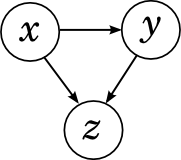
このケースも上記と同様です。 たとえば、エッジを
xから
yおよび
zに、また
yから
zに移動させます。 分解されます
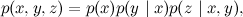
繰り返しますが、これはすべての共同分布に常に当てはまります
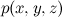
。 この式では、変数を任意の順序で選択できますが、何も変わりません。 ベイジアンネットワークでの方向ループは禁止されていることに注意してください。すべてのエッジを描画する方法のオプションの結果、8つではなく6つしかありません。
もちろん、これらの観察は、任意の数の変数の場合に一般化されます:変数が互いにまったく接続されていない場合、それらは独立しており、すべてのエッジが描画されるグラフ(任意の方向に矢印がありますが、有向サイクルは取得されません) 、分解に対応します。これは常に真実であり、情報を提供しません。
3つの変数を持つベイジアンネットワーク:興味深いケース
このセクションでは、さらに3つの興味深いケースを検討します。これらは、ベイジアンネットワークを構成できる「ブリック」です。 幸いなことに、これには3つの変数のグラフを考慮するだけで十分です。他のすべてはそれらから一般化されます。 以下の例では、「
xが
yに影響する」として、2つの変数間の矢印であるエッジを直観的に解釈します。 本質的に因果関係として。 実際、これはもちろん完全に真実ではありません-たとえば、多くの場合、意味を失うことなくエッジを展開できます(2つの変数のグラフでは、エッジをどのように描画するかは重要ではありません)。 そして一般的に、これは難しい哲学的質問です。「原因と効果の関係」とは何か、なぜ必要なのか。 しかし、指の推論のために行います。
シリアル通信
変数間のシリアル接続で開始します:
x “ affects”
y 、および
y 、次に“ affects”
zです。
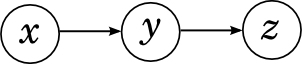
そのようなグラフは分解を示します

直観的には、これは一貫した因果関係に対応しています。冬に帽子なしで走ると風邪をひき、風邪をひくと体温が上がります。 明らかに、
xと
y 、および
yと
zは互いに接続されており、それらの間には矢印も直接描画されます。 このようなネットワークで
xと
zは接続されていますか、これらの変数は依存していますか? もちろん! 冬に帽子なしで走ると、高温になる可能性が高くなります。 ただし、このようなネットワークでは、
xと
zは
yを介してのみ接続され、
yの値が既にわかっている場合、
xと
zは独立します:風邪があることがすでにわかっている場合、それが何を引き起こしたかは関係なく、温度は上昇します(または上昇しません) )風邪から。
正式には、これは、条件
yの下での
xと
zの条件付き独立性に対応します。 これを確認しましょう:
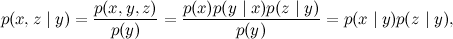
ここで、最初の等式は条件付き確率の定義、2番目は拡張、3番目はベイズの定理の適用です。
したがって、3つの変数間の一貫した関係は、極値変数が平均の条件の下で条件付きで独立していることを示しています。 すべてが非常に論理的で、かなり簡単です。
分岐接続
次の可能なオプションは分岐接続です:
xは
yと
zの両方に「影響」します。

そのようなグラフは分解を示します
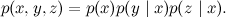
直観的には、これは同じ理由で2つの結果に対応します。風邪を引いた場合、体温が上昇し、鼻が切れることがあります。 前のケースと同様に、
xと
y 、および
xと
zが依存していることは明らかであり、問題は
yと
zの間にあります。 繰り返しますが、これらの変数が依存していることは明らかです。鼻水がある場合、風邪をひく可能性が高くなります。つまり、高温になる可能性も高くなります。
ただし、このようなネットワークでは、前のケースのように、
yと
zは
xを介してのみ接続されており、一般的な理由の意味がすでにわかっている場合、
x 、
yおよび
zは独立します。風邪があることがすでにわかっている場合、鼻水と温度は独立します。 免責事項:私の医療の例は非常にarbitrary意的であり、実際、風邪の場合に一般的な風邪と温度が独立しているかどうかはわかりません。 他の多くの病気も、これらの症状の両方を一緒に引き起こす可能性があります。 しかし、宇宙の条件付きモデルには、風邪以外の病気はありません。
正式には、これは条件
xの下での
yと
zの条件付き独立性に対応します。 これを確認することは、シリアル通信の場合よりもさらに簡単です。
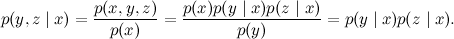
したがって、3つの変数間の分岐関係は、「結果」が条件付きで独立していることを示しています。ただし、「共通の原因」があります。 原因がわかっている場合、結果は独立します。 原因は不明ですが、それを介した結果はつながっています。 繰り返しますが、これまでのところ驚くべきことではないようです。
収束接続
3つの変数間の接続の可能なバリアントは1つだけです
。xと
yが一緒に
zに 「影響」する場合の収束接続。
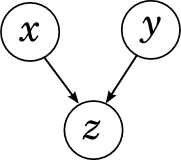
ここでの分解は次のとおりです。
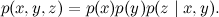
これは、同じ効果が2つの異なる原因を持つ可能性がある状況です。たとえば、温度は風邪の結果である場合があります。 寒さと中毒は依存していますか? いや! この状況では、一般的な効果は不明ですが、2つの理由は互いに関連しておらず、正式に検証するのは非常に簡単です。
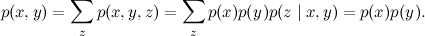
ただし、「一般的な効果」
zが
判明すると、状況は変わります。 現在、既知の結果の一般的な原因が互いに影響を及ぼし始めています。 この現象は、英語で説明することと呼ばれています。熱があることを知っているとします。 これにより、風邪と中毒の両方の可能性が大幅に高まります。 ただし、中毒になったことが判明した場合、風邪の可能性は低下します。症状は考えられる原因の1つに対して「すでに説明されている」ため、2番目の症状は起こりにくくなります。
したがって、収束する接続では、2つの「原因」は独立していますが、「共通の効果」の意味が不明な場合に限ります。 一般的な効果が示される場合、原因は依存します。
しかし、Vasily Ivanovichが述べたように、1つのニュアンスがあります。パス上で収束する接続が発生した場合、独立性を判断するために「一般的な効果」だけを調べるだけでは十分ではありません。 実際、
zに意味がなくても、その子孫の1つ(おそらくかなり遠い)に意味がある場合でも、2つの理由が依存します。 直感的には、これも理解しやすいです。たとえば、温度自体を観察するのではなく、その子孫である温度計の測定値を観察しましょう。 おそらく、世界には温度計に欠陥があるため、これは特定の確率的接続でもあります。 ただし、温度計の測定値を同じ方法で観察すると、風邪や中毒に依存します。
すべてをまとめる
非循環有向グラフを構成する3つのブリックは、シーケンシャル、収束、および発散ボンドです。 そして、このようなグラフすべてに対する条件依存性と独立性の結果を一般化するには、私たちの推論で十分です。 もちろん、これは一般的な定理を正式に証明する時間でも場所でもありませんが、結果は十分に予測可能です-2つの頂点(または2つの頂点のセット)が独立しているかどうかを大きなグラフで確認する必要があるとします。 これを行うには、これら2つの頂点セットを接続するグラフ内のすべてのパス(矢印を除く)を確認します。 これらの各パスは、上記のいずれかの構造によって「破損」する可能性があります。たとえば、中間に符号がある場合(変数の値がわかっている場合)、シリアル接続は切断され、符号がない場合は収束接続が切断されます(逆に、彼女の子孫ではなく、邪魔にならないように)。 その結果、すべてのパスが壊れている場合、変数のセットは本当に独立しています。 そうでない場合、いいえ。
そのため、今日は複雑な分布の因数分解の単純で便利で重要な表現であるベイジアンネットワークに注目しました。 次回は、別の(ただし、同様の)グラフィック表現を検討し、出力アルゴリズムの開発を開始します。 複雑な確率モデルのベイズ推論問題を解く。