Haskellのいくつかの変数の多項式とBuchbergerアルゴリズム

この記事では、Haskell言語でGrobnerベースに関連するアルゴリズムをどのように実装したかについてお話したいと思います。 誰かが私のアイデアや説明が役立つと思うことを願っています。 理論については説明しませんので、読者は多項式環の概念、環の理想、そして理想の基礎に精通している必要があります。 この ICMMOの本を読むことをお勧めします。それには、必要な理論がすべて詳細に説明されています。

この記事の主な主題は、いくつかの変数の多項式環の理想のグレブナー基底です。 この概念は、多項方程式のシステムを研究するときに生じます。 記事の最後で、これらのアイデアをどのように適用できるかを例で示します。

この理論が与える最も重要な結果は、いくつかの変数で方程式の多項式システムを解くための良い方法です。 高等代数やHaskellに精通していない場合でも、これらの同じ解法は学生がアクセス可能なレベルで説明されており、理論全体は正当化するためにのみ必要なので、この記事を読むことをお勧めします。 高等代数に関連するすべてを安全にスキップし、方程式系を解く方法を学ぶことができます。

興味があるなら、猫の下でお願いします。

申し訳ありませんが、これはラテックスでレンダリングされていますが、habrにstyle="width:...;height=...;"理解させる方法 知りません より良い方法を教えていただければ、間違いなくやり直します。

1代数から最も必要な概念

特定のルール（軸）に対応する「加算」と「乗算」の2つの操作を指定できる要素のセットは、代数のリングと呼ばれます。 係数が実数であるいくつかの変数の多項式は、 、多項式の加算および乗算の通常の学校操作に関連して。 リングの理想は、そのようなサブセットであり、その2つの要素の差はその中にあり、その要素のいずれかとリングの任意の要素の積はこのサブセットにあります。 理想の最も単純な例は、整数の環の理想としての複数の5つの数字のセットです。 これが理想的であることを確認してください。 うまくいけば、それ以上問題はありません。

さらに、多項式環の理想のみを考慮します。 多項式のいくつかの有限集合 理想の多項式が次のように表現できる場合、理想の基底と呼ばれます どこで -いくつかの多項式。 この事実は次のように書かれています。 。 ヒルベルトの基底定理は驚くべき結果をもたらします-（多項式環内の）理想には有限の基底があります。 これにより、あらゆる状況で作業することができ、理想の有限ベースで作業することができます。

次に、次の形式の連立方程式を考えます。



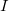
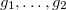
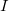
このシステムの理想を理想と呼びます 。 代数から理想的に横たわっている多項式は 元のシステムの任意のソリューションで消えます。 そしてさらに、 -理想のもう一つの基盤 その後、システム



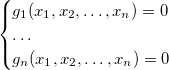
元のソリューションと同じ数のソリューションがあります。 このすべてから、システムの理想の中で元のものよりも単純な基礎を見つけることができれば、システム自体を解くタスクは単純化されることになります。

魔法のように、そのような基盤が存在します-それは理想のグレブナー基盤と呼ばれます。 定義上、これは、理想からの多項式の剰余（後で）を使用した除算手順がゼロ剰余を生成するような基礎です。 それを構築すると、その多項式の1つは、少なくともほとんどの場合、1つの変数のみに依存し、逐次置換によってシステム全体を解くことができます。

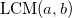
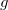
最後に必要なのは 多項式と基準 ブッフバーガーのカップル。 単項式を注文する「良い」方法を選択し（詳細については本を参照してください）、 多項式の上位項（この順序付けに関連） 、そして -単項式の最小公倍数 そして 。 それから -からの多項式 そして 次の構造が呼び出されます。



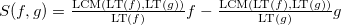
実証済み（基準 -pair）理想の基礎は、その場合にのみ、グレブナーの基礎である -そのメンバーの任意のペアからの多項式は、基底で除算したときに0の剰余を与えます（これについては以下で説明します）。 これにより、そのような基礎を構築するためのアルゴリズムが直ちに求められます。

1. 基底多項式の各ペアについて、それらを構成します -多項式で、それを基に剰余で除算します。
2. すべての剰余がゼロに等しい場合、グレブナー基底が取得されます。 そうでない場合は、ゼロ以外のすべての残差を基底に追加し、手順1に戻ります。

これがBuchbergerアルゴリズムです-この記事の主要な主題です。 それはすべて数学で、先に進むことができます。 何かを理解していない場合は、ウィキペディアまたは本をご覧ください。ただし、さらにナレーションを行うには高等代数の知識は必要ありません。

2 Haskellのいくつかの変数からの多項式の表現

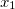
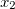
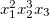
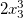
単項式から多項式の表現を構築し始めます。 単項式の特徴は、係数と変数の次数の2つだけです。 変数があると仮定します 、 などなど。 その後、単項式 係数は1および度[2,3,1]で、単項式 -係数2および次数[0,0,3] 。 ゼロ度に注意してください！ これらは、他のすべてのメソッドの実装に不可欠です。 一般に、（1つの問題の枠組み内で）すべての単項式の次数のリストは同じ長さである必要があります。 これにより、作業が大幅に簡素化されます。

「単項」型を、係数（型「 c 」）と度数のリスト（各型「 a 」）で構成される代数データ型として説明しましょう。

 data Monom ca = M c [a] deriving (Eq) 

単項式を互いに比較する必要があるため、 Ordクラスの具体例を作成します。 これは非常に単純であると同時に、単項式の「適切な」順序付けの規則に準拠しているため、通常の辞書式順序付けを使用します。 また、システムでの作業の便宜上、 Showクラスの具体例を作成します。

 instance (Eq c, Ord a) => Ord (Monom ca) where compare (M _ asl) (M _ asr) = compare asl asr instance (Show a, Show c, Num a, Num c, Eq a, Eq c) => Show (Monom ca) where show (M c as) = (if c == 1 then "" else show c) ++ (intercalate "*" $ map showOne $ (filter (\(p,_) -> p /= 0) $ zip as [1..])) where showOne (p,i) = "x" ++ (show i) ++ (if p == 1 then "" else "^" ++ (show p)) 

show関数はスマートにしようとします。1の場合は係数を表示せず、ゼロ次の変数も表示せず、変数の最初の次数も表示しません。 このように：

 *Main> M 2 [0,1] 2x2 *Main> M 1 [2,2] x1^2*x2^2 

show似た関数を作成するので、それがどのように機能するかを正確に説明する価値があります。 zip as [1..]使用して、各次数をその変数の数で、次にfilter (
(p _) -> p /= 0) filter (
(p _) -> p /= 0) filter (
(p _) -> p /= 0) 0度をshowOneをshowOneして各変数の説明を文字列にshowOne最後にData.List intercalateを使用して、乗算アイコンを散在させてすべてを接着します

これで、実際のタイプの多項式を説明する準備ができました。 これには、通常のリストに対するnewtypeラッパーが適しています。

 newtype Polynom ca = P [Monom ca] deriving (Eq) instance (Show a, Show c, Num a, Num c, Eq a, Eq c) => Show (Polynom ca) where show (P ms) = intercalate " + " $ map show ms 

今回は、すべての汚い作業がすでに単項式のタイプに隠されているため、 show関数は単純です。 次のように機能します。

 *Main> P [M 1 [3,1], M 1 [2,2], M 1 [1,1]] x1^3*x2 + x1^2*x2^2 + x1*x2 

将来的には、このリストの単項式は常に降順で格納されることに同意します（ Ordの実施形態の定義の意味で）。 これにより、いくつかの実装が簡単になります。

3多項式の操作

最も単純な操作はLT、ゼロと等しいかどうかのテスト、および数値の乗算です。 単項式の順序に関する合意から、最も古い単項式は常にリストの最初に来て、 headを使用して取得できることがわかります。 単項式は、係数がゼロの場合はゼロと見なされ、単項式を含まない場合は多項式と見なされます。 まあ、定数を掛けると係数が変わるだけです：

 lt :: Polynom ca -> Monom ca lt (P as) = head as zero :: (Num c, Eq c) => Monom ca -> Bool zero (M c _) = c == 0 zeroP :: Polynom ca -> Bool zeroP (P as) = null as scale :: (Num c) => c -> Monom ca -> Monom ca scale c' (M c as) = M (c*c') as 

2つの単項式は、係数のみが異なる場合に類似と呼ばれます。 それらについては、量が決定されます-係数を追加するだけで、次数は変更されません。

 similar :: (Eq a) => Monom ca -> Monom ca -> Bool similar (M _ asl) (M _ asr) = asl == asr addSimilar :: (Num c) => Monom ca -> Monom ca -> Monom ca addSimilar (M cl as) (M cr _) = M (cl+cr) as 

2つの単項式を乗算するには、各変数の次数を加算するだけです。 この操作は、優れたzipWith関数を使用して非常に簡単に実装zipWithます。 コードはそれ自体を物語っていると思います：

 mulMono :: (Num a, Num c) => Monom ca -> Monom ca -> Monom ca mulMono (M cl asl) (M cr asr) = M (cl*cr) (zipWith (+) asl asr) 

さらに興味深いのは、多項式の追加です。 この問題を再帰的に解決します。 自明なケース-2つのゼロ多項式（空のリスト）の合計は、ゼロ多項式に等しい。 多項式とゼロの合計はそれに等しくなります。 これで、両方の多項式を非ゼロと見なすことができます。つまり、各多項式を上位の項と残りの「テール」に分けることができます。 次の2つの場合があります。

1. シニアメンバーも同様です。 この場合、それらを追加し、結果（ゼロ以外の場合）をテールの合計に追加します。
2. シニアメンバーは似ていません。 次に、大きい方を選択します。 順序付け条件は、両方の多項式の裾に同様の単項式がないことを保証します。 したがって、選択した多項式のテールを別の多項式で折り畳み、この最大の単項式を最初に追加できます。

この再帰的な手順の結果として、再び順序付き多項式を取得し、コード自体を記述することに注意してください。

 addPoly :: (Eq a, Eq c, Num c, Ord a) => Polynom ca -> Polynom ca -> Polynom ca addPoly (P l) (P r) = P $ go lr where go [] [] = [] go as [] = as go [] bs = bs go (a:as) (b:bs) = if similar ab then if (zero $ addSimilar ab) then go as bs else (addSimilar ab):(go as bs) else if a > b then a:(go as (b:bs)) else b:(go (a:as) bs) 

多項式の乗算は、完全に自然な方法で取得されます。 単項式に多項式を掛けるのは非常に簡単ですmulMonoとmulMonoを使用して単項式のそれぞれに掛けます。 次に、2つの多項式の積に分布（「分布則」、括弧の開示）を適用し、最初の多項式のすべての単項式に2番目の多項式を乗算して結果を加算するだけでよいことがわかります。 同じmapを使用して乗算を行い、 addPoly foldl'およびaddPolyを使用しfoldl'結果をfoldl'ます。 これら2つの操作のコードは驚くほど短く、型の説明よりも短いです！

 mulPM :: (Ord a, Eq c, Num a, Num c) => Polynom ca -> Monom ca -> Polynom ca mulPM (P as) m = P $ map (mulMono m) as mulM :: (Eq c, Num c, Num a, Ord a) => Polynom ca -> Polynom ca -> Polynom ca mulM l@(P ml) r@(P mr) = foldl' addPoly (P []) $ map (mulPM r) ml 

それですべて、多項式に基本的なアクションを実装したので、先に進むことができます！

4剰余に基づく除算（削減）

単項式と言う 単項式で除算 そのような単項式が存在する場合 あれ 。 明らかに、これは各変数が 劣らず 。 したがって、すでにおなじみのzipWith関数と、素晴らしいand関数を使用して、分割可能性チェックを実装できます。 検証に加えて、実際の分割手順を簡単に取得できます。

 dividable :: (Ord a) => Monom ca -> Monom ca -> Bool dividable (M _ al) (M _ ar) = and $ zipWith (>=) al ar divideM :: (Fractional c, Num a) => Monom ca -> Monom ca -> Monom ca divideM (M cl al) (M cr ar) = M (cl/cr) (zipWith (-) al ar) 

係数タイプは除算を許可する必要があることに注意してくださいFractionalクラス。 憂鬱ですが、何もできません。
多項式を剰余のある基底に分割するアルゴリズムは、基本的に列による単純な学校の分割です。 基底の多項式の中で、最初の多項式は、配当の上位項が上位メンバーで除算されるように選択され、この多項式に上位メンバーの商を掛けたものが配当から差し引かれます。 減算の結果は新しい配当として取得され、プロセスが繰り返されます。 シニアメンバーがベーシスのシニアメンバーのいずれでも割り切れない場合、部門は完了し、最後の配当は剰余と呼ばれます。

主な除算手順、 reduceManyと呼びましょうreducableとreduce 2つの補助的なものが必要です。 最初の関数は、多項式が別の整数で割り切れるかどうかをチェックし、2番目の関数は除算を実行します。

 reducable :: (Ord a) => Polynom ca -> Polynom ca -> Bool reducable lr = dividable (lt l) (lt r) reduce :: (Eq c, Fractional c, Num a, Ord a) => Polynom ca -> Polynom ca -> Polynom ca reduce lr = addPoly lr' where r' = mulPM r (scale (-1) q) q = divideM (lt l) (lt r) 

減算する関数がないため、2番目の多項式に-1を掛けて加算するだけです-簡単です！ そして、これが除算アルゴリズム全体です。

 reduceMany :: (Eq c, Fractional c, Num a, Ord a) => Polynom ca -> [Polynom ca] -> Polynom ca reduceMany h fs = if reduced then reduceMany h' fs else h' where (h', reduced) = reduceStep h fs False reduceStep h (f:fs) r | zeroP h = (h, r) | otherwise = if reducable hf then (reduce hf, True) else reduceStep h fs r reduceStep h [] r = (h, r) 

reduceMany関数は、多項式を基底に分割しようとします。 分割が発生した場合、プロセスは続行し、それ以外の場合は終了します。 内部関数reduceStepは、除算できる最初の多項式を探して除算し、剰余と除算が行われたかどうかを示すフラグを返します。

5 Buchbergerアルゴリズム

そこで、この記事の主要部分であるブッフベルガーアルゴリズムの実装について説明します。 まだ持っていない唯一のものは、取得するための関数です -多項式。 その実装は非常にシンプルで、単項式の最小公倍数を見つけるための補助関数です。

 lcmM :: (Num c, Ord a) => Monom ca -> Monom ca -> Monom ca lcmM (M cl al) (M cr ar) = M (cl*cr) (zipWith max al ar) makeSPoly :: (Eq c, Fractional c, Num a, Ord a) => Polynom ca -> Polynom ca -> Polynom ca makeSPoly lr = addPoly l' r' where l' = mulPM l ra r' = mulPM r la lcm = lcmM (lt l) (lt r) ra = divideM lcm (lt l) la = scale (-1) $ divideM lcm (lt r) 

ここでは、両方の多項式に対応する単項式が乗算され、残りの除算の場合のように、2番目の多項式にも1がマイナスされます。
このアルゴリズムを実装する方法はたくさんあると確信しています。 また、実装が最適であるとか、十分に単純であるというふりもしません。 しかし、私はそれが好きで、それが機能し、それがすべてです。

私が使用したアプローチは、動的と呼ぶことができます。 基礎を2つの部分に分割します-すでにチェック（および追加）している部分 -すべてのペアの多項式-「 checked 」-これを行う必要があるのは「 add 」 アルゴリズムの1つのステップは次のようになります。

1. 2番目の部分から最初の多項式を取る
2. 一貫して構築する -それと最初の部分のすべての多項式との間の多項式、およびすべての非ゼロの剰余を2番目の部分の最後に追加
3. この多項式を最初の部分に移動します

2番目の部分が空になるとすぐに、最初の部分にグレブナー基底が含まれます。 このようなソリューションの利点は、それらが考慮されないことです -既にカウントおよびチェックされているペアからの多項式。 このプロセスの重要な機能はcheckOneです。 多項式（2番目の部分から）と両方の部分を取り、基底に追加する必要がある多項式のリストを返します。 最初の部分で単純な再帰を使用します。当然、ゼロの残基を追加しません。

 checkOne :: (Eq c, Fractional c, Num a, Ord a) => Polynom ca -> [Polynom ca] -> [Polynom ca] -> [Polynom ca] checkOne f checked@(c:cs) add = if zeroP s then checkOne f cs add else s:(checkOne f cs (add ++ [s])) where s = reduceMany (makeSPoly fc) (checked++add) checkOne _ [] _ = [] 

確かにこれはトリッキーなfoldl置き換えることができますが、これは演習として残しておきます。 これに基づいてグレブナー基底を構築することだけが残っています。 アルゴリズムステップの実装は、その説明を逐語的に繰り返します。ご自身で確認してください。

 build checked add@(a:as) = build (checked ++ [a]) (as ++ (checkOne a checked add)) build checked [] = checked 

多項式aは最初の部分に進み、そのゼロ以外のすべての残基が2番目になります。 確認するだけで十分です。 -2番目の部分の各多項式の多項式。最初の部分のみで、部分間の多項式の動きによる。 これからグレブナー基底を取得するには、多項式の1つを最初の部分に、残りを2番目に入れ、 makeGroebner関数で行われるbuild手順を適用するだけで十分であることに注意してください。

 makeGroebner :: (Eq c, Fractional c, Num a, Ord a) => [Polynom ca] -> [Polynom ca] makeGroebner (b:bs) = build [b] bs where build checked add@(a:as) = build (checked ++ [a]) (as ++ (checkOne a checked add)) build checked [] = checked 

6使用例

これらのすべての理論的構造は、これらの方法の実用的な応用を実証することなく、完全に役に立たないようです。 例として、3つの円の交点を見つける問題を考えてみましょう。これは、地図上での最も簡単な位置決めです。 円の方程式を方程式系として記述します。

。

角かっこを開くと、次の結果が得られます。



グレブナー基底を構築しましょう（より正確にするためにRationalタイプを使用しました）：

 *Main> let f1 = P [M 1 [2,0], M (-2) [1,0], M 1 [0,2], M (-26) [0,1], M 70 [0,0]] :: Polynom Rational Int *Main> let f2 = P [M 1 [2,0], M (-22) [1,0], M 1 [0,2], M (-16) [0,1], M 160 [0,0]] :: Polynom Rational Int *Main> let f3 = P [M 1 [2,0], M (-20) [1,0], M 1 [0,2], M (-2) [0,1], M 76 [0,0]] :: Polynom Rational Int *Main> putStr $ unlines $ map show $ makeGroebner [f1,f2,f3] x1^2 + (-2) % 1x1 + x2^2 + (-26) % 1x2 + 70 % 1 x1^2 + (-22) % 1x1 + x2^2 + (-16) % 1x2 + 160 % 1 x1^2 + (-20) % 1x1 + x2^2 + (-2) % 1x2 + 76 % 1 (-20) % 1x1 + 10 % 1x2 + 90 % 1 15 % 1x2 + (-75) % 1 

奇跡的に、すぐに答えを出す2つの線形方程式、ポイント（7.5）が得られました。 3つの円すべてにあることを確認できます。 そのため、3つの複雑な2次方程式のシステムの解を2つの単純な線形方程式に減らしました。 Gröbnerベースは、このようなタスクに非常に便利なツールです。

7考察と結論に関する質問

実際、この結果はさらに改善できます。 -多項式は、上級メンバーが互いに素でない多項式のペアに対してのみ考慮される必要があります。つまり、最小公倍数は単なる積ではありません。 一部の情報源は、このケースについて「多項式にはリンクがある」と言っています。 この最適化をmakeGroebner関数に追加します。

上位項が基底の他の多項式の上位項で除算された多項式が最終基底に該当する場合、除外できます。 このようなすべての多項式を除外した後に得られた基底は、 最小グレブナー基底と呼ばれます。 また、 任意の項が他の多項式の上位項で除算された多項式を考慮することもできます。 この場合、この多項式を別の除算の剰余で置き換えます。 このタイプのすべての可能な操作が実行される基盤は、 reduceと呼ばれます。 演習として、ベースの最小化と削減を実施します。

結論として、この記事を最後まで読んでくれたすべての人に感謝したいと思います。 私の話は多少面倒であり、コードは不完全であった（そして理解できないかもしれない）ことは知っていますが、Grobnerのベースに誰かが興味を持っていることを望みます。 少なくともいくつかの実際のタスクで私の成果のアプリケーションを見つけることができれば、私は非常に喜んでいます。

この記事のコードはすべてgistとして入手できます。