先日、空気流量を測定するためのデバイスをプログラムするタスクがありました。 測定要素として-センサーはどのメーカーであるかが明確ではなく、特性も適切なパラメーターもありません。 選択の余地はありませんでした。キャリブレーション特性を削除し、伝達関数「ADC-stream readings」を表示する必要がありました。
センサーは、ほとんどすべての測定機器と同様に、温度に非常に敏感であるため、さまざまな温度に対して一連の特性(最小3)を削除する必要がありました。
データはさまざまな方法でMathCadに入力できますが、転置された行ベクトルの形式でこれを行うことをお勧めします。

この後、「強い意志」の決定によって近似関数のタイプを設定し、各キャリブレーション特性を近似する必要があります。 したがって、私の関数は、任意の関数の線形結合の形で解を探しているlinfit関数を使用して、3次多項式で正常に近似され、3つの多項式の係数を取得しました。

結果の多項式によって「成功した」実験データがどのようにモデル化されるかを確認するには、グラフを作成できます。

さて、温度補正を導入するために、各多項式係数の温度依存性、すなわち オッズのためだけに上記を行います。 実験データは、係数と温度値そのものになります。 温度依存性が線形であることを本当に望んでいましたが、線形近似に不必要にlinfit関数を使用することは可能ですが、それでもなお:

最後に、次の形式で目的の依存関係が表示されます。
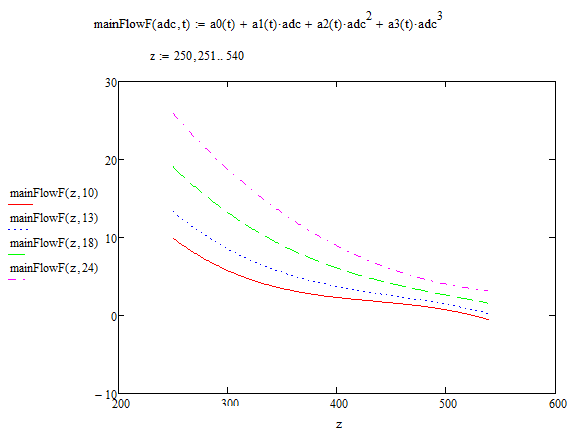
結果についてコメントすると、あまりうまく機能せず、率直に言ってうんざりしていました。 特性は当初、不十分な射撃で、通常のスタンドの欠如が影響を受けました。 一般に、キャリブレーションタスクはアマチュア的とはほど遠いものであり、膝の上で行うことはありません。 しかし、私はアプローチについて話したかった。