💆 👍🏿 👩🏾‍⚕️ 確率モデル：例と図 🎱 🤵🏿 📙

今日は前回始まったサイクルの2番目のシリーズです; 次に、有向グラフィカル確率モデルについて話し、この科学の主要な絵を描き、それらが対応する依存関係と独立性について議論しました。今日-前回の資料への一連のイラスト。いくつかの重要で興味深いモデルについて議論し、それらに対応する絵を描き、それらが対応するすべての変数の結合分布の因数分解を確認します。

単純ベイズ分類器

まず、前のテキストを簡単に繰り返します。このブログでは、単純なベイズ分類器についてすでに説明しました。単純ベイズでは、次のトピックを条件に、属性（単語）の条件付き独立性について追加の仮定が行われます。

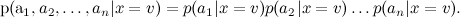
結果は複雑な事後分布です

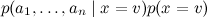
なんとか書き直した

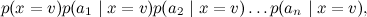
そして、このモデルの写真は次のように対応します。

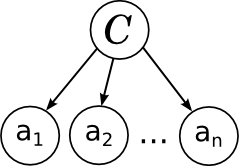
すべては前回述べたとおりです。ドキュメント内の個々の単語は、分岐リンクによって変数カテゴリに関連付けられています。これは、これらがこのカテゴリの条件の下で条件付きで独立していることを示しています。単純ベイズの学習は、個々の因子のパラメーターをトレーニングすることです：カテゴリーp （ C ）のアプリオリ分布と個々のパラメーターの条件付き分布

。

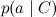
次に進む前に、写真についてもう1つ注意してください。モデルには非常に多くの場合、同じタイプの変数が多数あり、それらは同じ分布を持つ他の変数に関連付けられます（おそらく異なるパラメーターを持つ）。絵を読みやすく理解しやすくするために、無数の点や「点、これで完全な2部グラフ、わかりました」のようなものがないようにするには、同じタイプの変数をいわゆる「プレート」に結合すると便利です。これを行うには、伝播される変数の典型的な代表を配置する長方形を描画します。長方形の隅のどこかに、コピーの数を指定する方が便利です。

そして、すべてのドキュメントの一般的なモデル（サイコロなしでは描画しませんでした）は、このグラフの複数のコピーで構成され、したがって、次のようになります。

ここでは、カテゴリーαとパラメーター（各カテゴリーβの単語確率）の分布パラメーターを明示的に描画しました。これらのパラメーターは分解に個別の要因を持たないため、ネットワークノードはそれらに対応しませんが、明確にするためにそれらを描写することもしばしば便利です。この場合、図は、変数Cの異なるコピーが同じ分布p （ C ）から生成され、単語の異なるコピーが同じ分布から生成され、カテゴリの値によってパラメーター化されていることを意味します（つまり、βは行列異なるカテゴリの異なる単語の確率）。

線形回帰

統計のコースから漠然と思い出すことができる別のモデル、線形回帰を続けましょう。モデルの本質は単純です：予測したい変数yは、重みwを持つ線形関数として特徴ベクトルxから取得されると仮定します（太字のフォントはベクトルを示します-これは一般に受け入れられており、htmlでは、毎回よりも便利です矢印を描く）と正規分布ノイズ：

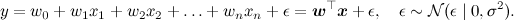
モデルは、データセットDのデータセットにアクセスできることを前提としています。この回帰自体の個別の実装で構成されており、（重要！）これらの実装は独立して生成されたと想定されています。さらに、線形回帰では、パラメーターのアプリオリ分布がしばしば導入されます-たとえば、正規分布

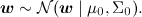
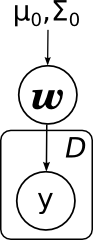
それからこの写真に行きます：

ここでは、アプリオリ分布μ0とΣ0のパラメーターを明示的に描画しました。注意してください-線形回帰は、構造が単純なベイに非常に似ています。

サイコロを使用すると、同じことがさらに簡単になります。

線形回帰で解決される主なタスクは何ですか？最初のタスクは、 wの事後分布を見つけることです。 Dからの利用可能なデータ（ x 、 y ）でwの分布を再計算することを学ぶ。数学的には、分布パラメータを計算する必要があります

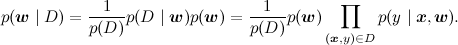
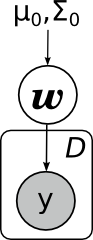
グラフィカルモデルでは、値がわかっている変数は通常影付きです。したがって、タスクは、証拠のあるこのようなグラフに従ってwの分布を再計算することです。

2番目の主なタスク（やや基本的な）は、予測分布を計算して、新しいポイントでyの新しい値を評価することです。数学的には、このタスクは前のタスクよりもはるかに複雑に見えます-事後分布を統合する必要があります

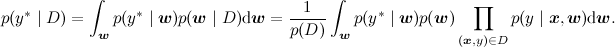
グラフィカルな変更はそれほど多くありません-予測したい新しい変数を描画しますが、タスクは同じです：（データセットからの）いくつかの証拠を使用して、モデル内の他の変数の分布を再計算します。：

隠れマルコフモデル

別の広く知られている人気のある確率モデルのクラスは、隠れマルコフモデル（HMM）です。これらは、音声認識、部分文字列のファジー検索、および他の同様のアプリケーションで使用されます。隠れマルコフモデルはマルコフチェーン（各変数x _{t + 1}が前のx _tのみに依存し、条件x _tが前のx _tkから条件付きで独立しているランダム変数のシーケンス）です。現在の状態に依存するいくつかの観測量y _t 。たとえば、音声認識では、隠された状態は言いたい音素であり（これはいくつかの簡略化であり、実際には各音素はモデル全体ですが、説明のために降りてきます）、オブザーバブルは実際には認識デバイスに到達する音波です。写真は次のとおりです。

この図は、既に準備された隠れマルコフモデルを適用する問題を解決するのに十分です：既存のモデル（隠れ状態A間の遷移確率、チェーンπの初期分布、オブザーバブルBの分布パラメーターで構成される）とこのオブザーバブルのシーケンスを使用して、最も可能性の高い隠れ状態のシーケンスを見つけます; すなわち、例えば、新しい音声ファイルを認識する既製の音声認識システムで。モデルのパラメーターをトレーニングする必要がある場合、すべての遷移に同じパラメーターが関係していることが明確になるように、それらを絵に明確に描く方が良いです：

LDA

すでに説明した別のモデルは、LDA（潜在ディリクレ割り当て、潜在ディリクレ割り当て）です。これは、テーマ別モデリングのモデルであり、各ドキュメントは、単純なベイのように1つのトピックではなく、可能なトピックの離散分布によって表されます。同じテキストで、生成LDAモデル-完成したLDAモデルでドキュメントを生成する方法については既に説明しました。

ドキュメントの長さNを選択します（これはグラフに描画されません-モデルのその部分ではありません）。
ベクトルを選ぶ -このドキュメントの各トピックの「表現度」のベクトル。
N個の単語wごとに：
- トピックを選択してください配布による ;
- 言葉を選ぶ βで与えられた確率で。

これで、対応する画像がどのように見えるかがわかります（そのブログ投稿にもありました。Wikipediaからもう一度コピーしますが、この画像の本質は上記のものとまったく同じです）。

SVDおよびPMF

一連の投稿（ 1、2、3、4 ）で、共同フィルタリングの主なツールの1つである特異行列分解、SVDについて説明しました。

勾配降下法を使用してSVD分解を検索しました。エラー関数を作成し、それから勾配を計算し、それに沿って下降しました。ただし、通常はPMF（確率的行列因子分解）と呼ばれる、問題の一般的な確率論的ステートメントを定式化できます。これを行うには、ユーザーと製品の特性のベクトルにアプリオリ分布を導入する必要があります。

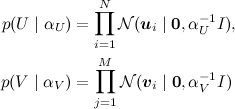
（ここで、 Iは単位行列です）、その後、通常のSVDの場合と同様に、ユーザー属性と製品属性のノイズの多い線形結合として評価を提示します。

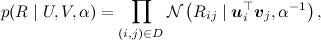
製品は、トレーニングサンプルにある評価に従って取得されます。この写真がわかります（写真は記事[Salakhutdinov、Mnih、2009]から取られました）：

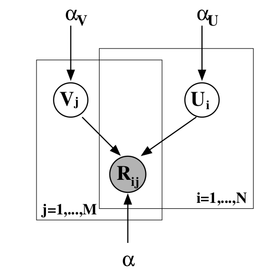
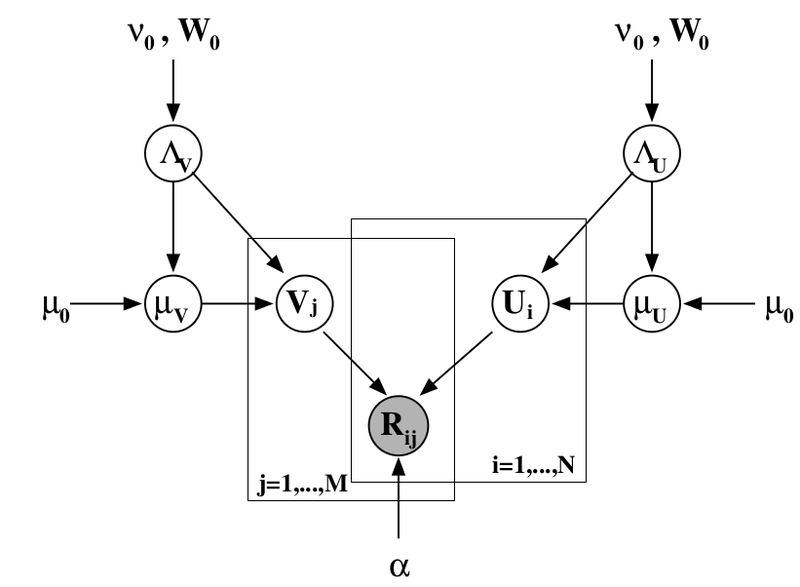
別のレベルのベイジアン推論を追加し、同時にユーザーと製品の属性分布のハイパーパラメーターをトレーニングできます。ここでは説明しませんが、対応する写真（同じ記事から）を提供するだけです。おそらく、これについてさらに話す機会があるでしょう。

ベイジアン評価システム

個人的に私に近いもう1つの例は、Alexander Sirotkinと私がBayesian評価システムの1つを改善したことです。おそらくブログの後半で、レーティングシステムについて詳しく説明します。しかし、ここでは最も単純な例を挙げます-チェスプレーヤーのEloレーティングはどのように機能しますか？近似値や魔法の定数に入らない場合、その本質は非常に簡単です。一般的に評価とは何ですか？評価はゲームの強さの尺度にしたいと思います。ただし、外部および内部のランダムな要因の影響下で、パーティーごとのゲームの強さが非常に大きく変化する可能性があることは明らかです。したがって、実際には、特定のゲームの1人または別の参加者のゲームの強さ（これらの力の比較がゲームの結果を決定します）はランダム変数であり、チェスプレーヤーのゲームの「真の強さ」は数学的な期待であり、評価はこの数学的な期待の不正確な評価です。とりあえず、特定のゲームにおける参加者のゲームの強さが、一定の一定の分散を備えた真の強さの周りに通常分布する最も単純なケースを考えます（エロの評価はそれだけです-したがって、彼の魔法の定数「200レーティングポイントのチェスプレイヤーは、ゲームごとに平均0.75ポイント」）。各ゲームの前に、各チェスプレーヤーのゲームの強さの先験的な推定値があります。また、アプリオリ分布も正規であり、それぞれパラメーターμ1、σ1およびμ2、σ2 _であるとします。私たちのタスク-ゲームの結果を把握し、これらのパラメーターを再カウントします。写真は次のとおりです。

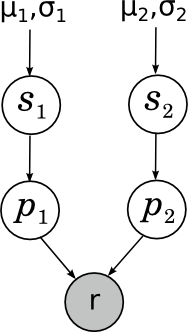
ここで、 s _i （スキル）はチェスプレーヤーの「ゲームの真の力」、 p _i （パフォーマンス）はこの特定のゲームに示されたゲームの力、 rはp ₁との比較から得られるゲームの結果を示すかなり興味深いランダム変数です。 p ₂ 。これについての詳細は、今日はしません。

インターネットユーザーの行動

そして、私に近い別の例-検索エンジンでのインターネットユーザーの行動パターンで終わります。繰り返しますが、詳細には触れません-多分これに戻りますが、たとえば、今のところ、レビュー記事をAlexander Fishkovで読むことができます。そのようなモデルの1つを例として考えます。ユーザーが検索結果を受け取ったときに何をするかをシミュレートしようとしています。ビューリンクとクリックはランダムイベントとして扱われます。特定の要求セッションの場合、変数E _iは、位置iに表示されるドキュメントへのリンクの説明を表示することを意味します。Ci-この位置をクリックします。簡単な仮定を導入します。説明を表示するプロセスは常に最初の位置から始まり、厳密に線形であると仮定します。ポジションは、以前のポジションがすべて表示された場合にのみ表示されます。その結果、仮想ユーザーはリンクを上から下へ読み、好きなら（リンクの関連性に依存します）、クリックし、ドキュメントが本当に関連していることが判明した場合、ユーザーは離れて戻りません。好奇心が強いが真実：検索エンジンにとって、良いイベントとは、ユーザーができるだけ早く立ち去って戻ってこなかったときであり、SERPに戻ったら、探しているものが見つからなかったことを意味します。

結果は、いわゆるカスケードクリックモデル（CCM）です。その中で、ユーザーは次のブロック図に従います。

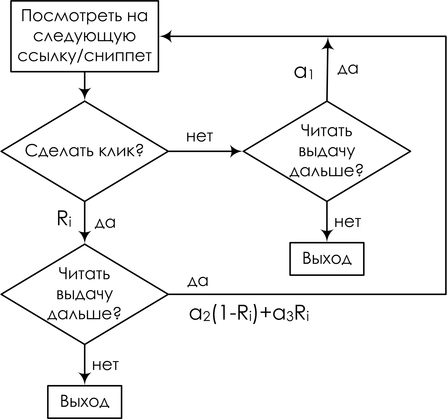
そして、ベイジアンネットワークの形で、次のように描くことができます。

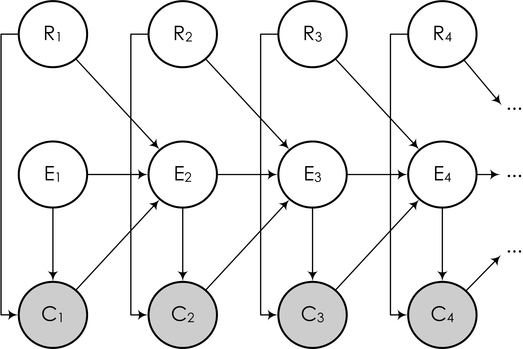
ここで、後続のイベントE _i （このイベントは「ユーザーが調べる」という単語からの「次のスニペットを読む」）は、前のリンクがクリックされたかどうかに依存します。タスクは再び上記と同じ方法で説明されます：変数の一部（ユーザークリック）を観察し、クリックに基づいてモデルをトレーニングし、各リンクの関連性に関する結論を引き出す必要があります（実際の関連性に従ってリンクをさらに並べ替えるには）。。モデル内の他のいくつかの変数の値について。

結論と結論

この記事では、指示されたグラフィカルモデルからロジックを簡単に「読み取る」確率モデルの例をいくつか調べました。さらに、確率モデルに通常必要なものは、かなり明確に定義された1つのタスクの形で表すことができると確信しました-有向グラフィックモデルでは、いくつかの変数の分布を他の変数の既知の値で再計算します。しかし、ロジックはロジックですが、実際にはどのように教えるのでしょうか？この問題を解決するには？それについて-次のシリーズ。

確率モデル：例と図