この記事に触発されて、簡単な二乗法を皆さんと共有することにしました。 平方は、数を乗算するよりもまれな操作ですが、非常に興味深いルールがあります。
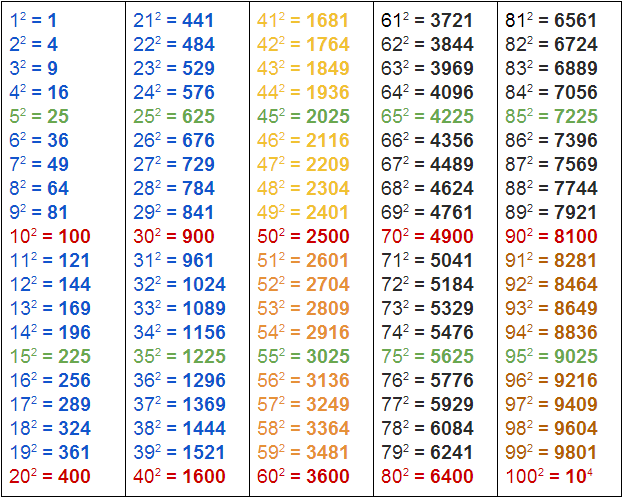*平方から数百数式に従ってすべての数値を無意識に二乗しないようにするには、次のルールを使用してタスクをできるだけ単純化する必要があります。
ルール1（10個の数字を切り捨てます）
0で終わる番号の場合。数字が0で終わる場合、それを掛けるのは1桁の数字と同じくらい簡単です。 ゼロをいくつか追加するだけです。
70 * 70 = 4900.
テーブルは赤でマークされています。
ルール2（10個の数字を切り捨てる）
5で終わる数字の場合5で終わる2桁の数値を2乗するには、最初の桁（x）に（x + 1）を掛けて、結果に「25」を追加する必要があります。
75 * 75 = 7 * 8 = 56 … 25 = 5625.
テーブルは緑色でマークされています。
ルール3（8つの数字を切り捨てます）
40から50までの数字の場合。 XX * XX = 1500 + 100 * + (10 - )^2
十分に難しいですよね？ 例を見てみましょう：
43 * 43 = 1500 + 100 * 3 + (10 - 3)^2 = 1500 + 300 + 49 = 1849.
テーブルは明るいオレンジ色でマークされています。
ルール4（8つの数字を切り捨てます）
50から60までの数字の場合。 XX * XX = 2500 + 100 * + ( )^2
また、知覚するのに十分困難です。 例を見てみましょう：
53 * 53 = 2500 + 100 * 3 + 3^2 = 2500 + 300 + 9 = 2809.
テーブルは濃いオレンジでマークされています。
ルール5（8つの数字を切り捨てます）
90から100までの数字の場合。 XX * XX = 8000+ 200 * + (10 - )^2
ルール3のように見えますが、異なる要因があります。 例を見てみましょう：
93 * 93 = 8000 + 200 * 3 + (10 - 3)^2 = 8000 + 600 + 49 = 8649.
テーブルには濃い濃いオレンジ色のマークが付いています。
ルール番号6（32個の数字を切り捨てます）
40個までの数字の2乗を覚えておく必要があります。ワイルドで難しいように聞こえますが、実際には、20個まではほとんどの人が2乗を知っています。 25、30、35、および40は、数式に適しています。 そして、16組の数字のみが残ります。 それらは、ニーモニック（後で説明します）を使用して、または他の方法で既に記憶されています。 乗算表のように:)
テーブルは青色でマークされています。
すべてのルールを記憶できますが、いずれの場合も、1〜100のすべての数値を選択して2つの式に従うことができます。 ルールは、これらの式を使用せずに、オプションの70％以上をすばやく計算するのに役立ちます。 これらの2つの式は次のとおりです。
数式（残り24個）
25〜50の数字
XX * XX = 100(XX - 25) + (50 - XX)^2
例：
37 * 37 = 100(37 - 25) + (50 - 37)^2 = 1200 + 169 = 1369
50から100までの数字の場合
XX * XX = 200(XX - 50) + (100 - XX)^2
例：
67 * 67 = 200(67 - 50) + (100 - 67)^2 = 3400 + 1089 = 4489
もちろん、合計の平方を拡張するための通常の式（
ニュートンの二項式の特殊なケース）を忘れないでください：
(a+b)^2 = a^2 + 2ab + b^2. 56^2 = 50^2 + 2*50*6 + 6*2 = 2500 + 600 + 36 = 3136.
更新100に近い数の積、特にその2乗も、「最大100の欠損」の原則に従って計算できます。
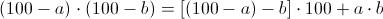
つまり、最初の数値から2番目の数値の「欠陥」を100に引き、「欠陥」の2桁の積を割り当てます。
正方形の場合、それぞれさらに簡単です。
92*92 = (92-8)*100+8*8 = 8464
（
sieloverから）
二乗は、家庭で最も有用なものではないかもしれません。 あなたが平方数を必要とするかもしれないとき、すぐにケースを思い出さないでください。 しかし、数字ですばやく動作し、各数字に適切なルールを適用する能力は、脳の記憶と「計算能力」を完全に発達させます。
ところで、habrのすべての読者は、64 ^ 2 = 4096、および32 ^ 2 = 1024であることを知っています。
数値の多くの正方形が連想レベルで記憶されます。 たとえば、88 ^ 2 = 7744を簡単に覚えましたが、これは同じ数字によるものです。 誰もが確かに自分の特性を持っています。
私は最初に「数学への13のステップ」という本で2つのユニークな公式を見つけました。それは数学とはほとんど関係がありません。 実際、以前（おそらく今）、ユニークなコンピューティング能力は風光明媚な魔法の数字の1つでした。魔術師はバイクに彼がどのように超大国を獲得したかを伝え、これの証拠として、数を数百から数百に即座に入れます。 この本は、立方体に直立する方法、根と立方根を差し引く方法も示しています。
クイックカウントのトピックが興味深い場合は、さらに書きます。
エラーと修正に関するメモは、事前にHPにご記入ください。