💘 🍳 ⚖️ 階乗より複雑なもの 🤰🏿 ⚙️ 👦🏾

むかしむかし、草が緑になり木が高くなると、ゼノセファルという名前のトロルが生きました。彼は原則として多くの場所に住んでいましたが、幸運なことに、あるフォーラムで彼に会うことができました。会話が行われたトピックも覚えていませんが、その本質は、XenocephalがLisp（マクロを含む）がすべての頭であり、テンプレートを備えたC ++が左手の悲惨な見た目であると周囲の人を説得しようとしたことです。また、ハードプレスされた階乗よりも複雑なものをプログラムすることは不可能であると主張されました。

私は原則として、Lispマクロがひどくクールであることに異議はありませんでした、そして、その時、私は答えることがありませんでしたが、C ++テンプレートと階乗についてのフレーズは私の壊れやすい脳に深く浸透し、内側から私を苦しめ続けました。そして、あるひどい日、私は思った：「一体何？プログラムしましょう！」

ドラゴンブックはもう一つのインスピレーションの源でした。タスクはすぐに見つかりました。非決定性ステートマシン（ NFA ）を決定性ステートマシン（ DFA ）に変換するアルゴリズムは、C ++テンプレートを使用して実装しようとするのに十分自明ではないことがわかりました。アレクサンドレスクの不朽の仕事により、彼はクリティカルマスを獲得することができました...

もちろん、私はプリミティブから始めました。私は何らかの形でグラフを表す必要がありました：

template <class T, int Src, int Dst, char Chr = 0> struct Edge { enum { Source = Src, Dest = Dst, Char = Chr }; typedef T Next; static void Dump(void) {printf("%3d -%c-> %3d\n",Src,Chr,Dst);T::Dump();} };

グラフの弧は、初期（Src）頂点と最終（Dst）頂点のインデックスで指定され、シンボル（Chr）で命名できます。（変換アルゴリズムで使用される）名前のないアークは、デフォルトでヌル文字でマークされます。このテンプレートで定義されたNextタイプは、タイプのリストに変換しました。このリストへのアークの追加は、次の再帰的な方法で実装されました。

 struct NullType {static void Dump(void) {printf("\n");}}; template <int S, int D, int C, class T, class R> struct AddEdge; template <int S, int D, int C, class R> struct AddEdge<S,D,C,NullType,R> { typedef typename Edge<R,S,D,C> Result; }; template <int S, int D, int C, class T, class R> struct AddEdge<S,D,C,Edge<T,S,D,C>,R> { typedef typename AddEdge<S,D,C,T,R>::Result Result; }; template <int S, int D, int C, int s, int d, int c, class T, class R> struct AddEdge<S,D,C,Edge<T,s,d,c>,R> { typedef typename AddEdge<S,D,C,T,Edge<R,s,d,c> >::Result Result; };

同様に、リストのマージが整理されました（グラフを表すものだけでなく、任意のカモタイピングのおかげです）。

追記

 template <class A, class B> struct Append; template <class T> struct Append<NullType,T> { typedef T Result; }; template <int S, int D, int C, class T, class B> struct Append<Edge<T,S,D,C>,B> { typedef typename Append<T,Edge<B,S,D,C> >::Result Result; };

参加する

 template <class A, class B> struct Join; template <class B> struct Join<NullType,B> { typedef B Result; }; template <int N, class T, class B> struct Join<Set<N,T>,B> { typedef typename Join<T,typename AddSet<N,B,NullType>::Result>::Result Result; }; template <int S, int D, int C, class T, class B> struct Join<Edge<T,S,D,C>,B> { typedef typename Join<T,typename AddEdge<S,D,C,B,NullType>::Result>::Result Result; }; template <int N, class S, class T, class B> struct Join<StateList<N,S,T>,B> { typedef typename Join<T,typename AddState<N,S,B,NullType>::Result>::Result Result; }; template <int Src, int Dst, int a, class S, class T, class B> struct Join<StateListEx<Src,Dst,a,S,T>,B> { typedef typename Join<T,typename AddState<Dst,S,B,NullType>::Result>::Result Result; };

...そして、リストの各要素に任意のファンクターを適用します：

地図

 template <class T, int V, class R, template <int,int> class F> struct Map; template <int V, class R, template <int,int> class F> struct Map<NullType,V,R,F> { typedef R Result; }; template <int N, class T, int V, class R, template <int,int> class F> struct Map<Set<N,T>,V,R,F> { typedef typename Map<T,V,Set<F<N,V>::Result,R>,F>::Result Result; }; template <class T, int S, int D, int C, int V, class R, template <int,int> class F> struct Map<Edge<T,S,D,C>,V,R,F> { typedef typename Map<T,V,Edge<R,F<S,V>::Result,F<D,V>::Result,C>,F>::Result Result; };

ここで、正規表現に基づいてNCAの構築を実装する必要がありました。この構造の手法自体は、上記の本で詳しく説明されており、詳細は、正規表現の要素が、名前のないアークで接続されたいくつかの基本構造に置き換えられているという事実に要約されています。

名前付きアークは基本的な方法で作成されます：

 template <char Chr> struct C { typedef typename Edge<NullType,0,1,Chr> Result; enum {Count = 2}; };

開始頂点と終了頂点は、それぞれインデックス0と1を受け取ります。

次のように2つのグラフを代替構造/ A | B /で接続できます。

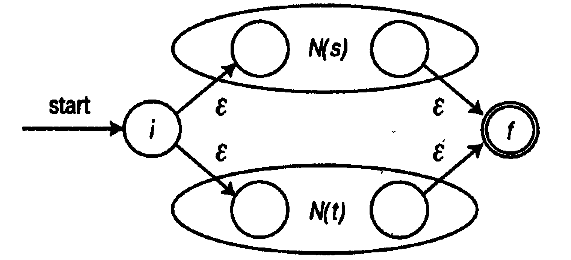
 template <int X, int N> struct Add { enum { Result = X+N }; }; template <class A, class B> struct DImpl { private: typedef typename Append< typename Map<typename A::Result, 2, NullType, Add>::Result, typename Map<typename B::Result, A::Count+2, NullType, Add>::Result >::Result N0; typedef typename Edge<N0,0,2> N1; typedef typename Edge<N1,0,A::Count+2> N2; typedef typename Edge<N2,3,1> N3; public: typedef typename Edge<N3,A::Count+3,1> Result; enum {Count = A::Count+B::Count+2}; }; template <class T1, class T2, class T3 = NullType, class T4 = NullType, class T5 = NullType> struct D: public DImpl<T1, D<T2,T3,T4,T5> > {}; template <class T1, class T2> struct D<T1,T2,NullType,NullType,NullType>: public DImpl<T1,T2> {};

ここでは、2つの入力グラフ（AとB）を「マージ」し（同時に頂点の番号を付け直します）、その後、上記の図に従って名前のないアークでそれらを接続します。開始頂点と終了頂点のインデックスはそれぞれ0と1です。

次の/ AB /の実装は、やや理解しにくいことが判明しました。

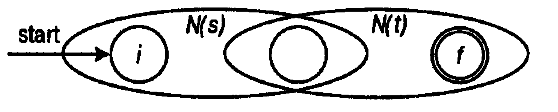
 template <int X, int N> struct ConvA { enum { Result = (X==1) ? (X+N-1) : X }; }; template <int X, int N> struct ConvB { enum { Result = (X==1) ? 1 : (X+N) }; }; template <class A, class B> struct EImpl { private: typedef typename Map<typename A::Result, A::Count, NullType, ConvA>::Result A1; typedef typename Map<typename B::Result, A::Count, NullType, ConvB>::Result B1; public: typedef typename Append<A1,B1>::Result Result; enum {Count = A::Count+B::Count}; }; template <class T1, class T2, class T3 = NullType, class T4 = NullType, class T5 = NullType> struct E: public EImpl<T1, E<T2,T3,T4,T5> > {}; template <class T1, class T2> struct E<T1,T2,NullType,NullType,NullType>: public EImpl<T1,T2> {};

ここでは、追加のアークは構築されず、グラフは共通の頂点で接続されます（Bの初期とAの最終）。

量指定子/ T * /の実装が最も難しいことが判明しました。

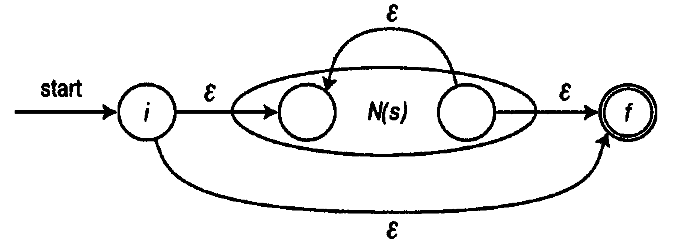
 template <class T, int Min = 0, int Max = 0> struct Q { Q() {STATIC_ASSERT(Min<=Max, Q_Spec);} private: typedef typename Map<typename T::Result, T::Count, NullType, ConvA>::Result A1; typedef typename Map<typename Q<T,Min,Max-1>::Result,T::Count,NullType,ConvB>::Result B1; public: typedef typename Edge<typename Append<A1,B1>::Result,0,T::Count> Result; enum {Count = T::Count+Q<T,Min,Max-1>::Count}; }; template <class T, int N> struct Q<T,N,N> { private: typedef typename Map<typename T::Result, T::Count, NullType, ConvA>::Result A1; typedef typename Map<typename Q<T,N-1,N-1>::Result, T::Count, NullType, ConvB>::Result B1; public: typedef typename Append<A1,B1>::Result Result; enum {Count = T::Count+Q<T,N-1,N-1>::Count}; };

量指定子/ T * /および/ T + /は非常に一般的であるため、最適化された実装はオーバーロードされました。

 template <class T> struct Q<T,1,1>: public T {}; template <class T> struct Q<T,0,0> { private: typedef typename Edge<typename Map<typename T::Result,2,NullType,Add>::Result,0,2> N0; typedef typename Edge<N0,3,1> N1; typedef typename Edge<N1,3,2> N2; public: typedef typename Edge<N2,0,1> Result; enum {Count = T::Count+2}; }; template <class T> struct Q<T,1,0> { public: typedef typename Edge<typename T::Result,1,0> Result; enum {Count = T::Count}; }; template <class T> struct Q<T,0,1> { public: typedef typename Edge<typename T::Result,0,1> Result; enum {Count = T::Count}; };

これで、本で説明されている正規表現/（a | b）* abb /を表すNFAを組み立てることができました。

 typedef E< Q< D< C<'a'>, C<'b'> > >, C<'a'>, C<'b'>, C<'b'> >::Result G;

DKAに変換するために残ります：

DFA

 enum CONSTS { MAX_FIN_STATE = 9 }; template <class Graph> class DFAImpl; template <class T, int Src, int Dst, char Chr> class DFAImpl<Edge<T,Src,Dst,Chr> >: public DFAImpl<typename T> { public: typedef typename DFAImpl<typename T>::ResultType ResultType; ResultType Parse(char C) { if ((State==Src)&&(C==Chr)) { State = Dst; if (State<MAX_FIN_STATE) { State = 0; return rtSucceed; } return rtNotCompleted; } return DFAImpl<typename T>::Parse(C); } void Dump(void) {T::Dump();} }; template <> class DFAImpl<NullType> { public: DFAImpl(): State(0) {} enum ResultType { rtNotCompleted = 0, rtSucceed = 1, rtFailed = 2 }; ResultType Parse(char C) { State = 0; return rtFailed; } protected: int State; }; //   ( )   ( a==0 - e-) // N -  // T -  // R -   // a -   template <int N, class T, class R, int a = 0> struct Move; template <int N, class R, int a> struct Move<N,NullType,R,a> {typedef R Result;}; template <int N, class T, int D, class R, int a> struct Move<N,Edge<T,N,D,a>,R,a> { typedef typename Move<N,T,typename AddSet<D,R,NullType>::Result,a>::Result Result; }; template <int N, int M, class T, int D, class R, int a, int b> struct Move<N,Edge<T,M,D,b>,R,a> { typedef typename Move<N,T,R,a>::Result Result; }; //     F // T -   (Set, StateListEx) //  -    F // R -   (Set, StateListEx) // F -  (Exist, NotExist, Important) template <class T, class C, class R, template <int,class> class F> struct Filter; template <class C, class R, template <int,class> class F> struct Filter<NullType,C,R,F> {typedef R Result;}; template <int N, class T, class C, class R, template <int,class> class F> struct Filter<Set<N,T>,C,R,F> { typedef typename If<F<N,C>::Result, typename Filter<T,C,typename Set<N,R>,F>::Result, typename Filter<T,C,R,F>::Result >::Result Result; }; template <int Src, int Dst, int a, class S, class T, class C, class R, template <int,class> class F> struct Filter<StateListEx<Src,Dst,a,S,T>,C,R,F> { typedef typename If<F<Dst,C>::Result, typename Filter<T,C,typename StateListEx<Src,Dst,a,S,R>,F>::Result, typename Filter<T,C,R,F>::Result >::Result Result; }; //  e- // T -    // G -  // R -    template <class T, class G, class R> struct EClos; template <class G, class R> struct EClos<NullType,G,R> {typedef R Result;}; template <int N, class T, class G, class R> struct EClos<Set<N,T>,G,R> { private: typedef typename Move<N,G,NullType>::Result L; typedef typename Filter<L,typename Append<T,R>::Result,NullType,NotExist>::Result F; public: typedef typename EClos<typename Append<T,F>::Result,G, typename Set<N,R> >::Result Result; }; //      // T -  // G -  // R -   // a -   template <class T, class G, class R, int a> struct MoveSet; template <class G, class R, int a> struct MoveSet<NullType,G,R,a> {typedef R Result;}; template <int N, class T, class G, class R, int a> struct MoveSet<Set<N,T>,G,R,a> { typedef typename MoveSet<T,G,typename Join<R,typename Move<N,G,NullType,a>::Result>::Result,a>::Result Result; }; //   ,      // N -    // K -     // T -  // n -   // S -   (Set) // G -  // R -     template <int N, int K, class T, int n, class S, class G, class R> struct MoveList; template <int N, int K, int n, class S, class G, class R> struct MoveList<N,K,NullType,n,S,G,R> {typedef R Result;}; template <int N, int K, int a, class T, int n, class S, class G, class R> struct MoveList<N,K,Set<a,T>,n,S,G,R> { private: typedef typename MoveSet<S,G,NullType,a>::Result S0; typedef typename EClos<S0,G,NullType>::Result S1; enum { N1 = (NotExist<1,S1>::Result)?K:N }; public: typedef typename MoveList<(N==N1)?(N+1):N, (K==N1)?(K+1):K, T,n,S,G, StateListEx<n,N1,a,S1,R> >::Result Result; }; //      NFA (    ) // T -  // R -   template <class T, class R> struct Alf; template <class R> struct Alf<NullType,R> {typedef R Result;}; template <class T, int S, int D, class R> struct Alf<Edge<T,S,D,0>,R> { typedef typename Alf<T,R>::Result Result; }; template <class T, int S, int D, int a, class R> struct Alf<Edge<T,S,D,a>,R>{ typedef typename Alf<T, typename AddSet<a,R,NullType>::Result>::Result Result; }; //    // T -   (StateListEx) // R -    // F -  (Exist, NotExist) template <class T, int R, template <int,class> class F> struct Incr; template <int R, template <int,class> class F> struct Incr<NullType,R,F> {enum {Result = R};}; template <int Src, int N, int a, class S, class T, int R, template <int,class> class F> struct Incr<StateListEx<Src,N,a,S,T>,R,F> { enum { Result = Incr<T, (F<1,S>::Result)?((N>=R)?(N+1):R):R, F>::Result}; }; //    // N -  // G -  template <int N, class G> struct Important; template <int N> struct Important<N,NullType> {enum {Result = (N==1)};}; template <int N, class T, int D> struct Important<N,Edge<T,N,D,0> > { enum { Result = Important<N,T>::Result }; }; template <int N, class T, int D, int C> struct Important<N,Edge<T,N,D,C> > { enum {Result = true}; }; template <int N, class T, int S, int D, int C> struct Important<N,Edge<T,S,D,C> > { enum { Result = Important<N,T>::Result }; }; //      // T -  // R -   template <class T, class R> struct ImportantOpt; template <class R> struct ImportantOpt<NullType,R> { typedef typename AddSet<1,R,NullType>::Result Result; }; template <class T, int S, int D, class R> struct ImportantOpt<Edge<T,S,D,0>,R>{ typedef typename ImportantOpt<T,R>::Result Result; }; template <class T, int S, int D, int C, class R> struct ImportantOpt<Edge<T,S,D,C>,R> { typedef typename ImportantOpt<T,typename AddSet<S,R,NullType>::Result>::Result Result; }; //       // A -   (Set) // B -   (Set) // G -  // I -    (    ) template <class A, class B, class G> struct EquEx { private: typedef typename Filter<A,G,NullType,Important>::Result A1; typedef typename Filter<B,G,NullType,Important>::Result B1; public: enum { Result = Equ<A1,B1>::Result }; }; template <class A, class B, class I> struct EquExOpt { private: typedef typename Filter<A,I,NullType,Exist>::Result A1; typedef typename Filter<B,I,NullType,Exist>::Result B1; public: enum { Result = Equ<A1,B1>::Result }; }; //    // G -  // R -   template <class T, class R> struct EdgeList; template <class R> struct EdgeList<NullType,R> {typedef R Result;}; template <class T, int S, int D, int C, class R> struct EdgeList<Edge<T,S,D,C>,R> { private: typedef typename AddSet<S,R, NullType>::Result R0; typedef typename AddSet<D,R0,NullType>::Result R1; public: typedef typename EdgeList<T,R1>::Result Result; }; //   (  ) // T -   (StateList) // S -   (Set) // I -    template <class T, class S, class I> struct ExistS; template <class S, class I> struct ExistS<NullType,S,I> {enum {Result = false};}; template <int N, class s, class T, class S, class I> struct ExistS<StateList<N,s,T>,S,I> { enum { Result = (Equ<s,S>::Result) ? // EquExOpt<s,S,I>::Result true : ExistS<T,S,I>::Result }; }; //     // T -   (StateListEx) //  -   (StateList) // I -    (Set) // R -   (StateListEx) template <class T, class C, class I, class R> struct FilterT; template <class C, class I, class R> struct FilterT<NullType,C,I,R> {typedef R Result;}; template <int Src, int Dst, int a, class S, class T, class C, class I, class R> struct FilterT<StateListEx<Src,Dst,a,S,T>,C,I,R> { typedef typename If<ExistS<C,S,I>::Result, typename FilterT<T,C,I,R>::Result, typename FilterT<T,C,I,StateListEx<Src,Dst,a,S,R> >::Result >::Result Result; }; //    // T -     (StateList) // a -      // S -   (Set) // I -    // R -   template <class T, int Src, int Dst, int a, class S, class I, class R> struct GenImpl; template <int Src, int Dst, int a, class S, class I, class R> struct GenImpl<NullType,Src,Dst,a,S,I,R> {typedef R Result;}; template <int n, class s, class T, int Src, int Dst, int a, class S, class I, class R> struct GenImpl<StateList<n,s,T>,Src,Dst,a,S,I,R> { typedef typename If<Equ<s,S>::Result, // EquExOpt<s,S,I> Edge<R,Src,n,a>, typename GenImpl<T,Src,Dst,a,S,I,R>::Result >::Result Result; }; //    // T -    //  -    // I -    // R -   template <class T, class C, class I, class R> struct Gen; template <class C, class I, class R> struct Gen<NullType,C,I,R> {typedef R Result;}; template <int Src, int Dst, int a,class S, class T, class C, class I, class R> struct Gen<StateListEx<Src,Dst,a,S,T>,C,I,R> { typedef typename Gen<T,C,I,typename GenImpl<C,Src,Dst,a,S,I,R>::Result>::Result Result; }; //   // N -     // K -     // G -  (NFA) // A -  (Set) // I -    (Set) // R -   (DFA) // M -    (StateList) // D -    (StateListEx) template <int N, int K, class G, class A, class I, class R, class M, class D> struct ConvertImpl; template <int N, int K, class G, class A, class I, class R, class M> struct ConvertImpl<N,K,G,A,I,R,M,NullType> {typedef R Result;}; template <int N, int K, class G, class A, class I, class R, class M, int Src, int Dst, int a, class S, class D> struct ConvertImpl<N,K,G,A,I,R,M,StateListEx<Src,Dst,a,S,D> > { private: typedef typename MoveList<N,K,A,Dst,S,G,NullType>::Result T; typedef typename StateList<Dst,S,M> M1; typedef typename Append<D,M1>::Result MD; typedef typename FilterT<T,MD,I,NullType>::Result T1; typedef typename AppendSafe<T1,D>::Result D1; typedef typename Gen<T,typename Append<T1,MD>::Result,I,R>::Result R1; enum { N1 = Incr<T1,N,Exist>::Result, K1 = Incr<T1,K,NotExist>::Result }; public: typedef typename ConvertImpl<N1,K1,G,A,I,R1,M1,D1>::Result Result; }; //  NFA -> DFA // G -  // R -   template <class G, class R> struct Convert { private: typedef typename Alf<G,NullType>::Result A; typedef typename ImportantOpt<G,NullType>::Result I; public: typedef typename ConvertImpl<1,MAX_FIN_STATE+1,G,A,I,NullType,NullType, StateListEx<0,0,0,typename EClos<Set<0,NullType>,G,NullType>::Result,NullType> >::Result Result; }; template <class T> class DFA: public DFAImpl<typename Convert<typename T::Result,NullType>::Result> {};

このコードのデバッグに関連するすべての試練（コンパイルエラーメッセージが含まれるキロメートル単位のリストのみが必要）の詳細については説明しません。アルゴリズムのフロントエンド実装がコンパイラーを完全にハングさせたため、最適化されたImportantOptテンプレートを実装する必要がありました。

これで、次のコードを実行できます。

  typedef E< Q< D< C<'a'>, C<'b'> > >, C<'a'>, C<'b'>, C<'b'> >::Result G; typedef Convert<G,NullType>::Result R; R::Dump();

...そして、生成される結果が以下であることを確認します。

  1 -a-> 10 1 -b-> 11 13 -a-> 10 13 -b-> 1 10 -a-> 10 10 -b-> 13 11 -a-> 10 11 -b-> 11 0 -a-> 10 0 -b-> 11

目的の列DKAに対応：

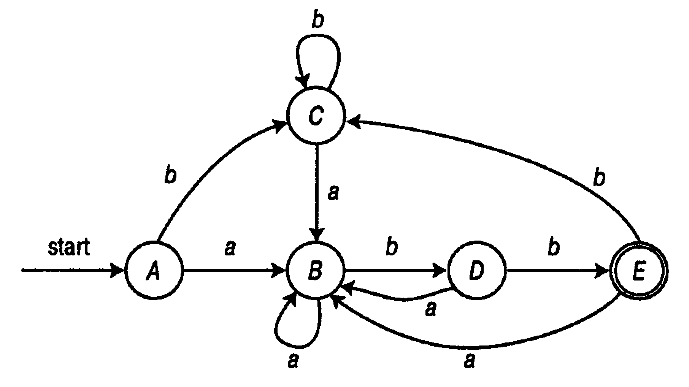
通常どおり、ソースはGitHubにアップロードされます。

階乗より複雑なもの

More articles: