4次元空間とは何かの説明から始めましょう。
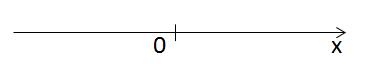
これは1次元の空間、つまりOX軸です。 その上の任意のポイントは、1つの座標によって特徴付けられます。
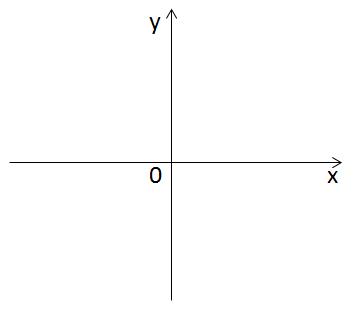
次に、OY軸をOX軸に垂直に描画します。 したがって、2次元空間、つまりXOY平面が得られました。 その上の任意の点は、横座標と縦座標の2つの座標によって特徴付けられます。
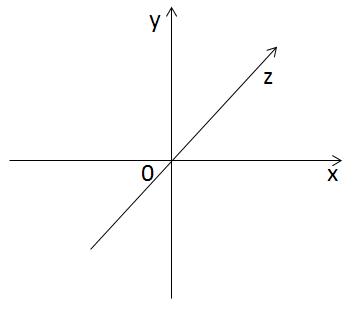
OZ軸をOXおよびOY軸に垂直に描画します。 結果は、任意のポイントに横座標、縦座標、およびプリプリケートがある3次元空間です。
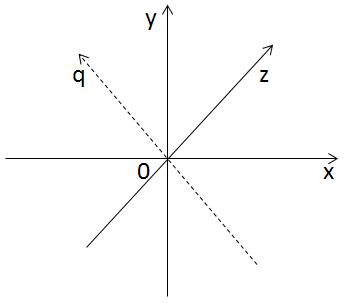
論理的に、4番目の軸であるOQは、OX、OY、およびOZ軸に同時に垂直である必要があります。 しかし、そのような軸を正確に構築することはできません。したがって、それを想像しようとするだけです。 4次元空間の各ポイントには、x、y、z、qの4つの座標があります。
次に、4次元の立方体がどのように表示されるかを見てみましょう。
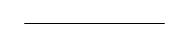
写真は一次元空間の図、つまり線を示しています。
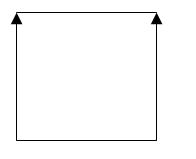
この線をOY軸に沿って平行移動し、結果の2本の線の対応する端を接続すると、正方形になります。
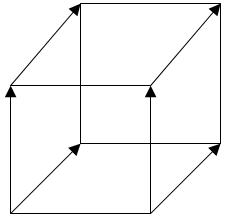
同様に、OZ軸に沿って正方形の平行移動を行い、対応する頂点を接続すると、立方体が得られます。
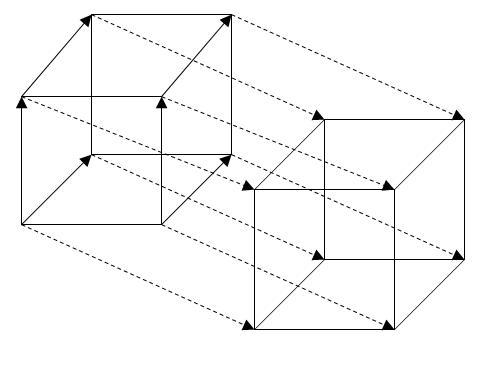
そして、OQ軸に沿って立方体の平行移動を行い、これら2つの立方体の頂点を接続すると、4次元の立方体が得られます。 ところで、それは
tesseractと呼ばれます。
平面に立方体を描くには、
それを
投影する必要があります。 これは視覚的に次のようになります。
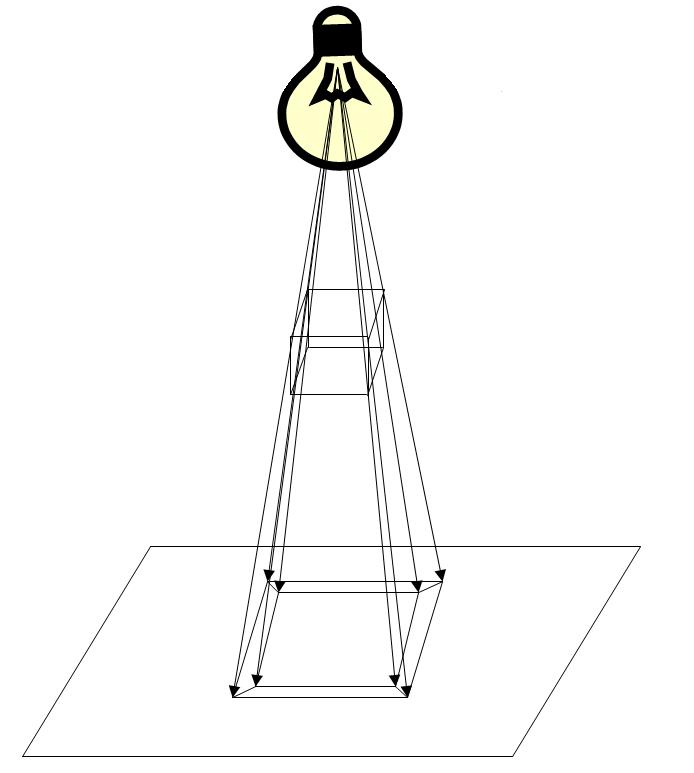
表面上の空中に立方体の
フレームモデルがぶら下がっていると想像してください。つまり、まるで「ワイヤーでできている」かのように、その上は電球です。 電球をオンにし、立方体の影の周りに鉛筆を描画し、電球をオフにすると、立方体の投影が表面に表示されます。
もう少し複雑な話に移りましょう。 もう一度、電球で図面を見てください。ご覧のように、すべての光線が一点に収束しました。 これは
消失点と呼ばれ
、 透視投影を作成するために使用されます(すべての光線が互いに平行の場合、平行になることもあります。結果はボリュームの感覚ではありませんが、より明るく、消失点が投影されたオブジェクトから十分に離れている場合、これらの2つの予測はほとんど目立ちません)。 消失点を使用して特定の点を特定の平面に投影するには、消失点と特定の点を通る線を引き、結果の線と平面の交点を見つける必要があります。 そして、より複雑な図形、たとえば立方体を投影するには、各頂点を投影してから、対応するポイントを接続する必要があります。
空間を部分空間に投影する
アルゴリズムは 、3D-> 2Dだけでなく、4D-> 3Dの場合に一般化できることに注意してください。
先ほど言ったように、OQ軸がどのように見えるか、tesseractも正確には想像できません。 しかし、ボリュームに投影して、コンピューター画面に描画すると、限定的なアイデアを得ることができます!
次に、tesseractの投影について説明します。
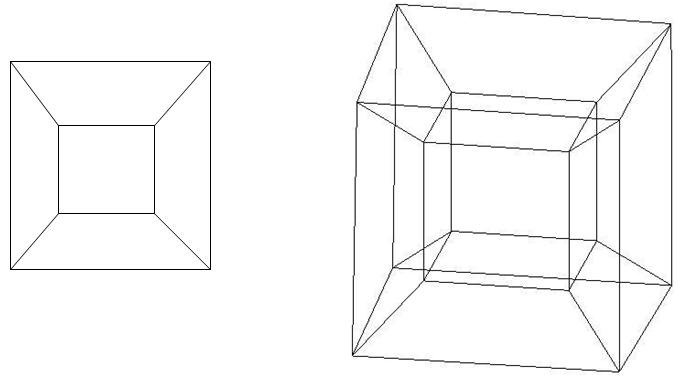
左側は立方体の平面への投影であり、右側はボリューム上のテッセラクトです。 これらは非常によく似ています。立方体の投影は、大小2つの正方形のように見え、一方が他方の内側にあり、対応する頂点が線で接続されています。 そして、テッセラクトの投影は、大小2つの立方体のように見え、一方が他方の中にあり、対応する頂点が接続されています。 しかし、私たちはすべて立方体を見ました。小さな正方形と大きな正方形の両方、および小さな正方形の上、下、右および左の4つの台形は実際には正方形であり、さらにそれらは等しいと確信できます。 そして、テセラクトは同じです。 そして、大きな立方体と小さな立方体、小さな立方体の側面にある6つの角錐台-これらはすべて立方体であり、同時にです。
私のプログラムは、体積にテセラクトの投影を描くだけでなく、回転させることもできます。 これがどのように行われるかを検討してください。
まず、どの
回転が平面に平行であるかを説明します。
立方体が軸OZの周りを回転することを想像してください。 次に、その頂点のそれぞれは、軸OZの周りの円を記述します。
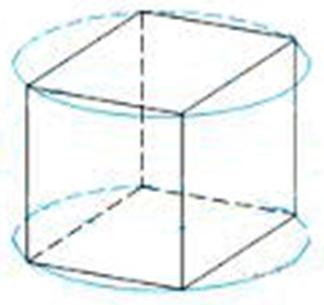
そして、円は平らな図です。 そして、これらの各円の平面は互いに平行であり、この場合、XOY平面に平行です。 つまり、OZ軸の周りの回転だけでなく、XOY平面に平行な回転についても話すことができますXOY軸に平行に回転する点については、横座標と縦座標のみが変化します。 3次元空間を扱っている場合にのみ、直線の周りの回転について話すことができます。 2次元ではすべてが点を中心に、4次元では-平面を中心に、5次元空間ではすべてボリュームの周りを回転します。 そして、ポイントの周りの回転を想像できるなら、平面とボリュームの周りの回転は考えられないものです。 そして、平面に平行な回転について話す場合、n次元空間では、点は平面に平行に回転できます。
あなたの多くは、おそらく回転行列について聞いたことがあるでしょう。 ポイントにそれを掛けると、角度phiだけ平面に平行に回転したポイントが得られます。 2次元空間の場合、次のようになります。
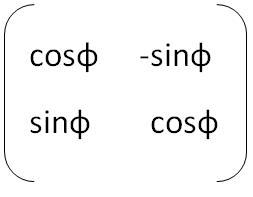
乗算方法:角度phiで回転したポイントのx =角度phiのコサイン*初期ポイントのxマイナス角度phiのサイン*初期ポイントのゲーム。
角度phiで回転したポイントのプレーヤー=角度phiのサイン*初期ポイントのx +角度phiのコサイン*初期ポイントのゲーム
Xa` = cosph * Xa-sinph * Ya
Ya` = sinph * Xa + cosph * Ya
ここで、XaとYaは回転するポイントの横座標と縦座標であり、Xa`とYa`は既に回転したポイントの横座標と縦座標です
3次元空間の場合、この行列は次のように一般化されます。

XOY平面に平行な回転。 ご覧のとおり、Z座標は変化せず、XとYのみが変化します
Xa` = cosph * Xa-sinph * Ya + Za * 0
Ya` = sinph * Xa + cosph * Ya + Za * 0
Za` = Xa * 0 + Ya * 0 + Za * 1(本質的にZa` = Za)

XOZ平面に平行な回転。 新しいものは何もない
Xa` = cosph * Xa + Ya * 0-sinph * Za
Ya` = Xa * 0 + Ya * 1 + Za * 0(実際にはYa` = Ya)
Za` = sinph * Xa + Ya * 0 + cosph * Za

そして3番目のマトリックス。
Xa` = Xa * 1 + Ya * 0 + Za * 0(本質的にXa` = Xa)
Ya` = Xa * 0 + cosph * Ya-sinph * Za
Za` = Xa * 0 + sinph * Ya + cosph * Za
4番目の次元については、次のようになります。

あなたはすでに何を掛けるべきかを理解していると思うので、私はそれを二度と描きません。 しかし、3次元空間の平面に平行な回転のマトリックスと同じことをしていることに注意してください! それとこれは両方とも縦座標とアプリケーションのみを変更し、残りの座標は変更されません。したがって、4番目の座標に注意を払わずに、3次元の場合に使用できます。
しかし、投影式はそれほど単純ではありません。 フォーラムをどれだけ読んだとしても、どの投影法も私にふさわしくない。 投影は立体的に見えないので、Parallelは私には不向きでした。 一部の射影式では、ポイントを見つけるために、方程式系を解く必要があります(しかし、コンピューターにそれらを解く方法を教える方法がわかりません)、私は他の人を理解しません...一般的に、私は自分の方法を考え出すことにしました このための投影2D-> 1Dを考えてください。
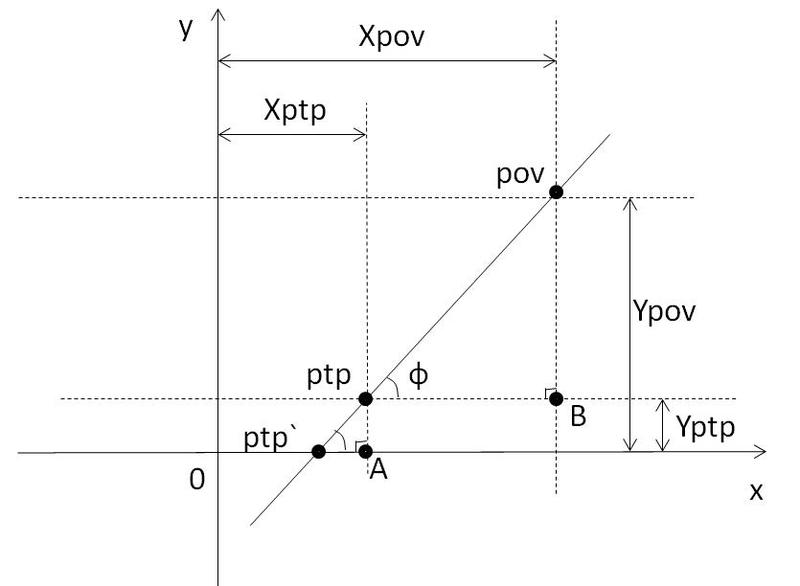
povは「視点」を意味し、ptpは「投影する点」(投影する点)を意味し、ptp`はOX軸上の目的の点です。
角度povptpBとptpptp`Aは対応するものと等しくなります(破線はOX軸に平行で、直線povptpは割線です)。
ポイントptp`のxは、ポイントptpのxからセグメントptp`Aの長さを引いたものに等しい。 このセグメントは、三角形ptpptp`Aから見つけることができます:ptp`A = ptpA /角度ptpptp`Aのタンジェント。 この接線はpovptpB三角形から見つけることができます:角度の接線ptpptp`A =(Ypov-Yptp)(Xpov-Xptp)。
回答:Xptp` = Xptp-Yptp /角度ptpptp`Aのタンジェント。
ここでは、このアルゴリズムの詳細については説明しませんでした。式が多少変更される特殊なケースが多いためです。 誰にそれが面白い-プログラムのソースコードを見て、すべてがコメントに記載されています。
3次元空間のポイントを平面に投影するには、2つの平面(XOZとYOZ)を考慮するだけで、それぞれについてこの問題を解決します。 4次元空間の場合、XOQ、YOQ、およびZOQの3つの平面をすでに考慮する必要があります。
そして最後に、プログラムについて。 これは次のように機能します:tesseractの16の頂点を初期化->ユーザーが入力したコマンドに応じて、回転->ボリュームに投影->ユーザーが入力したコマンドに応じて、投影を回転->平面に投影->描画
プロジェクションとターンを自分で書きました。 これらは、先ほど説明した式に従って機能します。 OpenGLライブラリは線を描画し、色を混ぜます。 そして、tesseractの頂点の座標は次のように計算されます。
原点と長い2-(1)および(-1)を中心とする線の頂点の座標。
-"-"-正方形-"-"-および長さ2のエッジ:
(1; 1)、(-1; 1)、(1; -1)および(-1; -1);
-「-」-キューブ-「-」-:
(1; 1; 1)、(-1; 1; 1)、(1; -1; 1)、(-1; -1; 1)、(1; 1; -1)、(-1; 1 ; -1)、(1; -1; -1)、(-1; -1; -1);
ご覧のとおり、正方形はOY軸の1つ上の線とOY軸の1つ下の線です。 立方体は、XOYプレーンの前に1つの正方形があり、その後ろに1つあります。 tesseractは、XOYZボリュームの反対側にある1つのキューブと、これにある1つのキューブです。 しかし、この単位とマイナス単位が列に書かれていれば、この交互の単位を知覚する方がはるかに簡単です
1; 1; 1
-1; 1; 1
1; -1; 1
-1; -1; 1
1; 1; -1
-1; 1; -1
1; -1; -1
-1; -1; -1
最初の列では、1と1の代替があります。 2番目の列には、最初に2つのプラスがあり、次に2つのマイナスがあります。 3番目では、4プラス1、そして4マイナス1です。 これらはキューブの上部です。 tesseractにはそれらの2倍の数があるため、それらを宣言するためのサイクルを記述する必要がありました。そうしないと、混乱しやすくなります。
私のプログラムはアナグリフの描き方も知っています。 3Dメガネの幸せな所有者は、立体画像を観察できます。 絵を描くのにトリッキーなことは何もありません。右目と左目のために、平面に投影されるのは2つだけです。 しかし、プログラムははるかに視覚的で興味深いものになり、最も重要なのは、4次元の世界についてのより良いアイデアを提供することです。
あまり重要ではない機能-顔の1つを赤で強調表示して、曲がり具合とマイナーなアメニティをよりよく見えるようにします-「アイ」ポイントの座標を調整し、回転速度を増減します。
プログラム、ソース、および使用説明書をアーカイブ:
www.dropbox.com/s/xilxouqmgnsf6zs/%D0%A2%D0%B5%D1%81%D1%81%D0%B5%D1%80%D0%B0%D0% BA%D1%82.rar (Dropboxプログラムをダウンロードしてインストールする必要があります:
www.dropbox.com )
ソース:
docs.google.com/document/d/1sGjBTb-od84Qp_la0LS9tWFZL4aYk-1exUs0Za5_Uq0/edit