著者からこの記事では、配列をソートするためのアルゴリズムの1つを検討します。 初心者または何らかの理由でこのアルゴリズムに慣れていない人を対象としています。 修正と修正は大歓迎です:)
理論挿入ソートは、単純なソートアルゴリズムです。 その本質は、アルゴリズムの各ステップで、配列の要素の1つを取得し、挿入および挿入する位置を見つけるという事実にあります。 1番目の要素の配列はソート済みと見なされることに注意してください。
アルゴリズムの口頭での説明はかなり複雑に聞こえますが、実際には実装するのが最も簡単なソートです。 私たちはそれぞれ、アクティビティのタイプに関係なく、ソーティングアルゴリズムを使用しましたが、それを認識しませんでした:)たとえば、ウォレットで紙幣をソーティングするとき-私たちは100ルーブルを取り、見ます-10、50、500ルーブル紙幣があります。 これはちょうど50から500の間で、私たちは100を挿入します:)または、すべての本から例を示します-カード "Fool"をプレイします。 デッキからカードを引くとき、昇順に並べられたカードを見て、描かれたカードの価値に応じて、適切な場所にカードを置きます。 明確にするために、ウィキペディアからアニメーションを提供します。
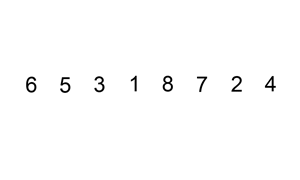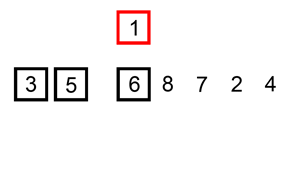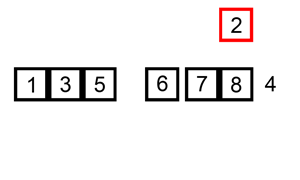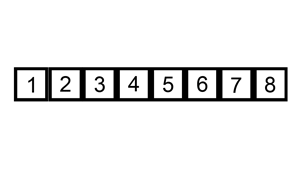 実装
実装実装を進める前に、入力データの形式を決定します。たとえば、これは整数(int)値の配列になります。 配列の要素の番号付けは0から始まり、n-1で終わります。 アルゴリズム自体はC ++で実装されています。 それでは始めましょう...
アルゴリズムのメインループは0番目の要素からではなく、1番目から開始します。これは、1番目の要素までの要素が並べ替えられたシーケンスになり(1つの要素の配列が並べ替えられることを思い出してください)他のみんな。 実際のコード:
for(int i=1;i<n;i++) for(int j=i;j>0 && x[j-1]>x[j];j--)
ソートの実装は非常に単純で、3行のみです。 スワップ関数は、要素x [j-1]とx [j]を交換します。 ネストされたループは、挿入する場所を探しています。 このアルゴリズムを覚えておくことをお勧めします。そうすれば、必要に応じて、バブルによる並べ替えを損なわないように並べ替えを記述できます:)
パフォーマンス分析挿入ソートの複雑さはn
2で、比較の数は式n *(n-1)/ 2を使用して計算されます。 証明のために、次のコードが作成されました。
void Sort(int* arr,int n){ int counter=0; for(int i=1;i<n;i++){ for(int j=i; j>0 && arr[j-1]>arr[j];j--){ counter++; int tmp=arr[j-1]; arr[j-1]=arr[j]; arr[j]=tmp; } } cout<<counter<<endl; }
100要素の順列の数:
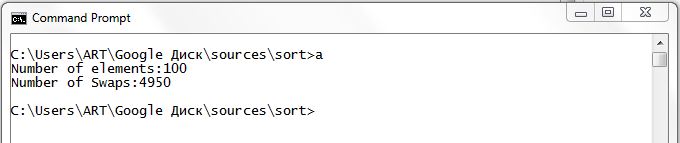
したがって、n = 100の場合、順列の数は4950であり、式n
2を使用して計算した場合、10000ではありません。 ソートアルゴリズムを選択するときは、このことに留意してください。
有効性挿入ソートは、配列がすでに部分的にソートされており、配列要素が多くない場合に最も効果的です。 要素が10個未満の場合、このアルゴリズムが最適です。 高速ソート(ボブセジウィック最適化)が補助として挿入ソートアルゴリズムを使用することは無駄ではありませんが、このアルゴリズムについては後で説明します...