前のパートでは、新しい型を設定し、それらの値に対して関数を作成する方法を学びました。 この短い記事では、研究のためのさらなるトピックを明確にして概要を説明するために、帰納的定義についてさらに詳しく説明します。
Coqにはバッテリーがないと先ほど言った。 実際、私はcでした-Coqには、多くの有用な定義を含む標準ライブラリがあります。 標準ライブラリに加えて、今のところ説明しない特定の事柄があります。
CoqIDEの開始時に、一部のライブラリはバックグラウンドでフレンドになります。そのリストは、[
Print Librariesコマンドを使用して表示できます。
ロードおよびインポートされたライブラリファイル:
Coq.Init.Notations
Coq.Init.Logic
Coq.Init.Datatypes
Coq.Init.Specif
Coq.Init.Peano
Coq.Init.Wf
Coq.Init.Tactics
Coq.Init.Prelude
Coq.Init.Logic_Type
学術目的のために、これらのライブラリの定義は使用しません。
ご存じのように、関数型プログラミングの入門記事では、階乗を計算しないと何もできません。 この伝統から逸脱することはなく、帰納的なタイプの独自の階乗を書きます。
自然数
帰納的定義は数学のいたるところにあります。 たとえば、集合論の観点からの自然数は次のように導入されます。
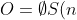&space;=&space;n&space;\cup&space;\left&space;\{&space;n&space;\right&space;\})
同様に、Coqで自然数を定義できます。 名前空間を詰まらせないために、モジュールシステムを使用します。
モジュールテスト1。
誘導ナット:タイプ:=
| O:nat
| S:nat-> nat。
この発表は次のようになります。
- Oは自然数、
- Sは正の整数を取り、別の正の整数を返すコンストラクターです。n∈Nの場合、S n∈Nです。
この定義を使用して、任意の自然数を作成できます。
Eval simpl in(SO)。
(* ==> 1:nat *)
Eval simpl in(S(SO))。
(* ==> 2:nat *)
(S(S(SO)))の簡易評価。
(* ==> 3:nat *)
自然数が得られたので、次はこれらの数の上に一連の関数を定義します。
Fixpoint plus(n:nat)(m:nat):nat:=
nに一致
| O => m
| S n '=> S(プラスn' m)
終わり。
ここで、入力として
nat型の2つの引数を取り、
nat型の結果を返す再帰(
Fixpointキーワード)
plus関数を定義しました。
Checkコマンドでこれを確認できます:
チェックプラス。
(* ==> plus:nat-> nat-> nat *)
特定の例での彼女の仕事を考えてみましょう。 式3 + 2の値を計算します。
Eval simpl in(プラス(S(S(SO)))(S(SO)))。
(* ==> 5:nat *)
いいね! すべてが機能します。 しかし、これはどのようになりますか?
(*プラス(S(S(SO)))(S(SO))
==> S(プラス(S(SO))(S(SO)))定義の2番目の節
==> S(S(プラス(SO)(S(SO))))定義の2番目の句
==> S(S(S(プラスO(S(SO)))))定義の2番目の節
==> S(S(S(S(S(SO))))は定義の最初の句です
*)
同様の方法で、乗算関数を記述し、階乗計算を実装できます。これがなければ、関数型プログラミングに関する単一の教科書ではできません。
固定小数点マルチ(nm:nat):nat:=
nに一致
| O => O
| S n '=> plus m(マルチn' m)
終わり。
固定小数点階乗(n:nat):nat:=
nに一致
| O => SO
| S n '=> mult n(階乗n')
終わり。
Eval simpl in(階乗(S(S(S(S(S(SO))))))。
(* ==> 120:nat *)
おわりに
素材を統合するには、読者がCoqIDEのすべての例を実行することを強くお勧めします。 次のパートでは、基本的なCoq戦術の使用を検討します。
継続する 。