目次
1.ダイナミクスの方程式はじめに

むかしむかし、私は次のコメントを書きました:
それだけです。
そのようなニュースの後、私は座って私のクアドロコプターを作ります。 そして、彼らは皆それをしますが、私はしません。 いいえ、しかし何。
いつも何かを飛んで欲しいと思っていました。 2機のラジコンヘリコプターがありました。 しかし、それはひどく終わった。
私はquadrocopterを作ることにしました。 それがどのように終了するか-表示されます。 既製のフライトコントローラーは使用せず、すべてを自分でプログラムします。 そして、このプロセスを一連の記事で説明しようとします。 今、私はあなたの注意に最初の部分を示します。 それは、ダイナミクスの方程式がクアドロコプター内に隠されていることを簡単に示します。
行きましょう。
1.運動方程式の導出
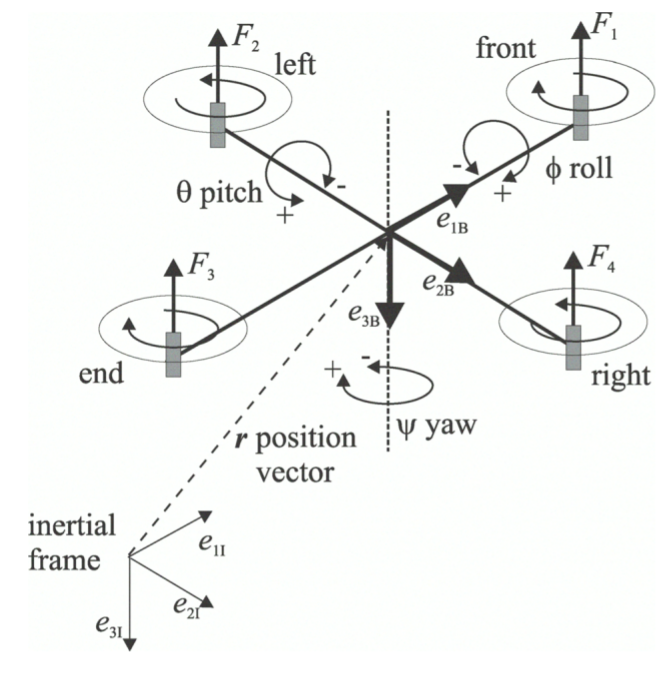
空間内のクアドロコプターの向きは、ヨー-ψ、ピッチ
-θ 、ロール
-φの 3つの角度によって決まります。
一緒にベクターを構成します。
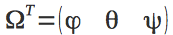
。
慣性基準システム内のデバイスの位置は、半径ベクトルによって設定されます
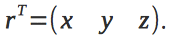
。
クアドロコプターの座標系から慣性座標系への遷移行列の形式は次のとおりです。
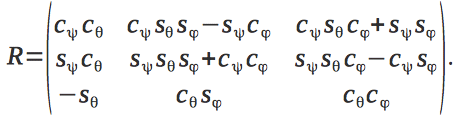
4つのエンジンのそれぞれによって生成される牽引力は、
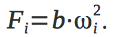
ここで、
ωiはエンジンの角速度、
bは比例係数です。
これで、垂直軸に沿ったクアドロコプターの加速度を記述する微分方程式を書くことができます。
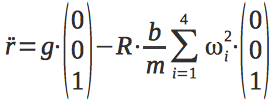
すぐに2番目の微分方程式を書きます
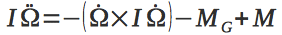
ここで、
Iは慣性行列、
Mはクアドロコプターに加えられるトルク、
M Gはジャイロモーメントです。
ベクトル
Mは次のように定義されます。
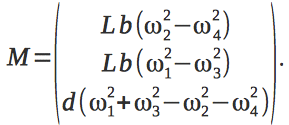
ここで、
dは抗力係数、
Lは肩の長さです。
エンジンの回転ローターを使用した物体の回転によって生じるジャイロモーメントは、次のように記述されます。
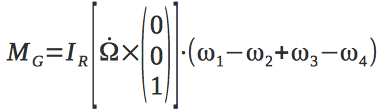
クアドロコプターを制御する4つの制御信号を紹介します。
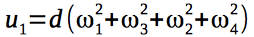
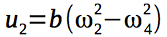
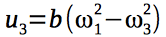
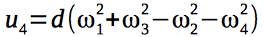
クアドロコプターに作用するジャイロモーメントは、エンジンのローターの角速度に依存するため、制御ベクトルに依存します
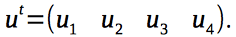
システムを記述する方程式系を作成します。
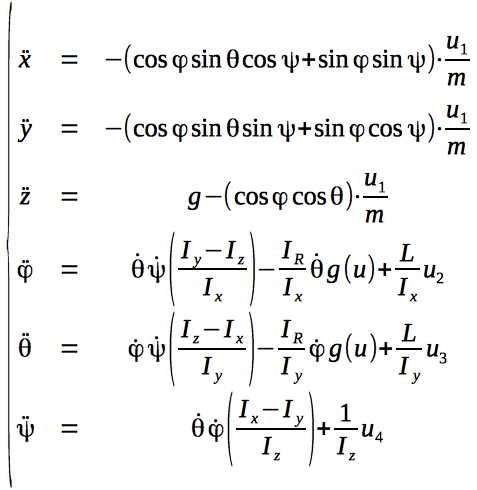
そして今、二次導関数がないようにシステムを変換しています。
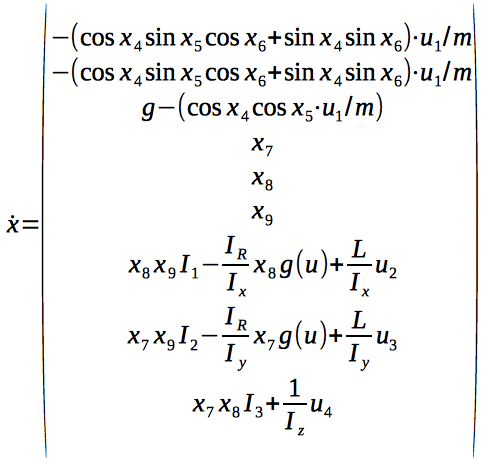
この9つの方程式からなるシステムは、システムのダイナミクスを説明しています。
おわりに
投稿はややいことが判明しました。
オンラインの数式エディタを教えてください。 そして、これらは非常に嫌に見えます。
質問の提案は大歓迎です!