大部分は口コミで伝えられる問題のクラスがあり、それらは数学的民間伝承の一部であると言うかもしれません。 非常に美しい解決策に問題がある場合があります。 あなたは決定を見て、推論のすべてのステップを理解しているように見えますが、だまされたように感じます。 あなたはすべてを理解すると同時に、何も理解しません。 たとえば、次のような錯視で類推を描くことができます。
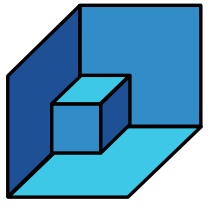
ここでは、切り取った部分のある大きな立方体と、隅にある小さな立方体が見えます。
この投稿では、お気に入りのタスクのいくつかを収集しましたが、その解決策は、感情のこのとらえどころのない二元論を引き起こすようです。
サークルと定規
ルーラーを1つだけ使用すると、平面に描かれた円の中心を見つけることができないことを証明します（ルーラーの長さは無限であると考えられています。平面上の任意のポイントを接続できます。ルーラーにはスケールがなく、その上にマークを付けることはできません）。
解決策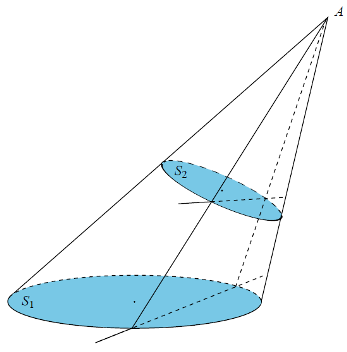
底面が特定の円である傾斜円錐を考えます
。 円錐は傾斜しているため、底面と平行ではなく、円錐から2番目の円を切り取る平面が存在します。
。
コーンの上に電球を置きます。 この光は、「上の」円の平面にある各線に影を落とします。
「下」の円の平面へ
。 さらに、直線の影も直線になります。 この影は「上」の円を表示するという事実にもかかわらず非常に注意が必要であることに注意してください
「下」へ
、「上」の円の中心の影は「下」の中心に落ちません。
ここで、1つのルーラーを使用して円の中心を見つける方法を説明するような素晴らしいアルゴリズムがあることを少し想像してみましょう。 このアルゴリズムは、コンピュータープログラムを読み取り、次のようなアクションのシーケンスで構成する必要があります：任意の直線を描画し、2番目の任意の直線を描画し、そのような交差点をそのような点に接続し、この直線と円のこの交差点を他の点に接続しますなどなど...「上部」平面でこの奇跡のアルゴリズムを使用して円の中心を見つけると、
、このアルゴリズムの「シャドウ」は「下部」平面でまったく同じコマンドを実行します。 そして、アルゴリズム（コマンドのセット）が円の中心を見つけると仮定したため、まったく同じコマンドを実行するアルゴリズムの「影」は下の円の中心を見つけなければなりません。 前に述べたように、見つかった「上」の円の中心の影は「下」の円の中心には入らないため、すぐに矛盾が生じます。
モスクワ地下鉄のタスク
モスクワの地下鉄には、高さ、幅、奥行きの合計が大きいアイテムの持ち込みを禁止するルールがあります
長方形の箱について話していることに同意しましょう。 システムをだましてボックスを完全に押すことができないことを証明します。
cm、測定値の合計が少ないボックス内
好きなように斜めに斜めに箱を積み重ねることができますが、しわにすることはできません。
解決策この決定は、
Hovhannes Khudaverdyanから私に伝えられました。
私たちの証明には、コンセプトが必要です
体に
腫れ 。 空間で任意の物体を取ります
-バフ研磨は、ボディ上または以下の距離にあるポイントのセットです
彼から。 言いましょう
-空間内のバルーニングポイントは半径のボールになります
、そして
-膨張は、ソーセージのように見える体になります。
今、私たちの箱（箱とその内側）を寸法で取ります
、
そして
、およびボリューム、それぞれ、
。 ボリュームを計算してみましょう
彼女
膨満感。 これで
-バンピングが含まれます：
- 箱自体 ;
- 箱の端で成長します。 箱の総表面積を
、これらの成長の量は 
。
- 箱の端で成長します。 このような成長はそれぞれ、ベースの半径を持つ円柱の1/4です。 。 長さのあるボックスには4つのリブがあるので 、 そして 、その後、同じrib骨の4つからの成長を1つの固体シリンダーに結合できます。 結果の3つのシリンダーの合計体積は
;
- ボックスの上部での成長。 このような成長はそれぞれ、半径のボールの8分の1です 。 したがって、ボックスの8つの頂点すべての上の成長から、半径の1つのボール全体を収集できます。 、つまりボリューム
。
そのボリュームを取得します
-ボックスの光沢は等しくなります
今、側面の寸法でボックスにしましょう
、
そして
2つ目の箱があります
、
そして
。 どんな数であってもそれを明確にする
取らなかった
-内箱のインフレーションは内にあります
-外部ボックスのインフレーション。そのため、その体積は少なくなります。
ボリュームの表現を不等式に置き換え、同じ用語を減らし、すべてを
：
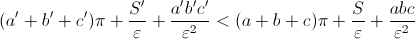
最後の不等式は、
小規模および大規模の両方。 したがって、いつでも限界に行くことができます
私達は得る：
したがって、1つのボックスが2番目のボックスにある場合、その寸法の合計はそれ以上にならないことを証明しました。
レンガの壁
非常に多くの異なる長方形（2次元ブリック）があり、各ブリックが整数の長さを持つ少なくとも1つの辺を持っていると想像してください。 そのようなレンガから、平らな長方形の壁が構築され、オーバーレイや穴がなく、レンガは傾斜していません。 結果の壁の少なくとも片側の長さが整数であることを証明します。
解決策問題を解決する前に、関数の1つの大きな特性を思い出しましょう
：長さが数の倍数であるセグメント上の積分
ゼロに等しい。 本当に
さらに、関数の積分
ゼロからある数まで
ゼロに等しい場合、安全に数を仮定することができます
複数
。
同様に、「水平圧縮」関数の場合
、長さが1の倍数（整数）であるセグメントの積分はゼロに等しくなります。
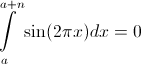
次に、関数を考えます
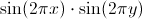
（原点を壁の左下隅に配置します）。 この関数には、壁のレンガに対する積分がゼロになるような素晴らしい特性があります。
実際、結局のところ、右側の積分の1つは、長さが整数であるためゼロに等しいセグメントに渡されます。
素晴らしい機能の不可欠な要素が
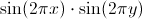
壁のレンガのいずれかがゼロに等しいため、これらのレンガで構築された壁全体では、各レンガの積分の合計であるため、この積分はゼロに等しくなります。 取得するもの：
そうか
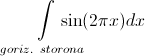
、または
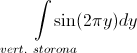
ゼロでなければなりません。 そこからすぐに、壁の水平または垂直の側面のいずれかが全長になります。
（
更新：読者が示唆するように、問題には少なくとも
14の解決策があります ）
井戸の仕事
丸い井戸が畑に掘られました。 さまざまな無限に長いボードがあります。 各ボードには独自の幅があります。 そして、隙間が残らないように、これらのボードでウェルを完全に閉じました（ボードは必ずしもすべて互いに平行ではありません）。 ボードの幅の合計が常にウェルの直径以上になることを証明します。
解決策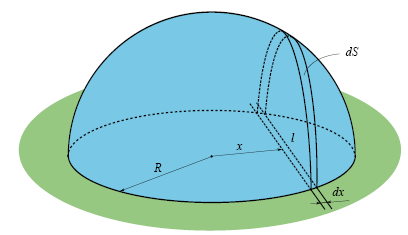
私の判断が間違っていなければ、その決定は
Alexander Karabegovに属します。
図に示すように、ウェルを半球で覆い、ウェルに巨大なスポットライトを設置します。これは平行な垂直光線で照らされます。 そして、非常に薄い、幅の広いボードを検討してください
それは井戸の上にあります。
ウェルの中心からボードの距離が遠いほど、長さが短くなることに注意してください
、これは井戸の真上にあるボードによって占められていますが、同時に、このボードからの半球内の影の傾斜角はより急になります。 これらの2つのプロセスは互いにキャンセルし、シャドウエリア
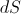
井戸の中心からのボードの距離とは無関係。 確かに、井戸の上のボードの長さ
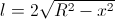
、そして影の勾配は
。 面積の式を取得します
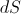
ボードの影。これは、影の長さと幅の積に等しくなります。
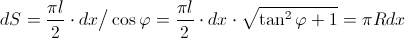
実際、非常に薄い板が井戸の上の広いところでは
面積
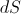
その半球の影は常に等しくなります
、つまり、ボードの幅のみに依存します
。 この「独立性」の特性は、幅の広いボードでも満たされます。これは、多くの薄いボードが固定されていると想像できるためです。 その結果、素晴らしい結果が得られます。井戸の上のボードの幅が
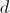
それから彼女の影の領域
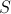
等しい
。
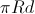
今、多くの板を広くしましょう
私たちの井戸を完全に覆います。 もちろん、厚板の一部は、幅全体がウェルの上にない場合があります。 したがって、各ボードの影の領域
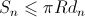
。 異なるボードはオーバーラップできるため、シャドウエリア全体
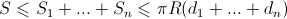
しかし、ボードは隙間なく井戸を覆っているので、それらの一般的な影は半球全体を埋めます。
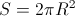
。 結果として、
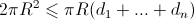
証明するために必要でした。