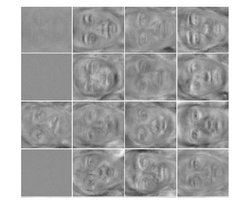
良い一日。 このトピックは、限られたボルツマンマシン(制限付きボルツマンマシン、RBM)のアイデアと、事前トレーニングニューラルネットワークでの使用を考えている人向けに設計されています。 その中で、実際の世界から撮影した画像を操作するために限定されたボルツマンマシンを使用する機能を検討し、標準タイプのニューロンがこのタスクに適していない理由とその改善方法を理解し、人間の顔の感情の表現を実験としてわずかに認識します。 RBMについてまったく知らない人は、特にここから入手できます。
c#で
制限付きボルツマンマシンを実装する制限付きボルツマンマシンを使用したニューラルネットワークトレーニングなぜすべてが悪いのか
限られたボルツマンマシンはもともと、可視および隠れの両方の確率的バイナリニューロンを使用して開発されました。 このようなモデルを使用してバイナリデータを操作することは非常に明白です。 ただし、実際の画像の大部分はバイナリではなく、0〜255の各ピクセルの整数の輝度値を持つ少なくともグレーの陰影で表されます。問題の考えられる解決策の1つは、輝度値を間隔0..1(255で除算する)に変更することです)、およびピクセルが実際にバイナリであり、取得された値が各特定のピクセルを1に設定する確率を表すと仮定します。 このアプローチを手書き認識(
MNIST )と
出来上がりに使用してみましょう-すべてがうまく動作し、素晴らしい動作をします! なぜすべてが悪いのですか?
しかし、多くの実際の画像では、特定のピクセルの強度は、ほとんど常に隣接ピクセルの強度と正確に等しいためです。 したがって、強度は、平均に近い確率が高く、平均から少し離れている確率が低い必要があります。 シグモイド(ロジスティック)関数では、このような分布を実現することはできませんが、重要でない場合(手書き文字など)になる場合があります
[1] 。
それを良くする方法...
強度が、たとえば0.61に等しい可能性が最も高い、たとえば0.59または0.63である可能性が低く、0.5または0.72である可能性が非常に低いと言える可視ニューロンを表現する方法が必要です。 確率密度関数は次のようになります。
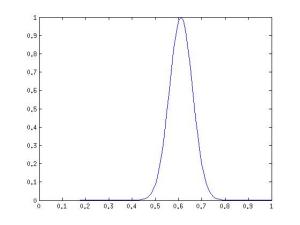
はい、これは
正規分布です! 少なくとも、このようなニューロンの動作をシミュレートするために使用できます。これは、可視ニューロンの値を
ベルヌーイ分布で
はなく正規分布でランダム変数にすることで
行います。 正規分布は、実際の画像だけでなく、範囲[-∞; +∞]の実数で表される他の多くのデータでも使用するのに便利であり、値を範囲からバイナリ形式または確率に減らすことは意味がないことに注意してください[0; 1]
[2] 。 この場合、隠されたニューロンはバイナリのままであり、いわゆるガウスバイナリRBMを取得します。これは、式
[3]で与えられるニューロンの値の分布です
。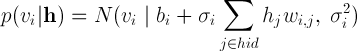
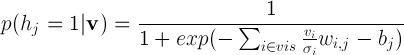
ボルツマン機械のエネルギーは
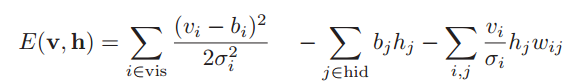 hid
hidは隠れニューロンのインデックスのセットです。
vis-可視ニューロンの多くのインデックス、
b-バイアス(オフセット)、
σiはi番目の可視ニューロンの標準偏差です。
w i、jは、i番目とj番目のニューロン間の接続の重みです。
N(x |μ、σ2)は、期待値μおよび分散σ2の正規分布を持つ変数のxの値の確率です。
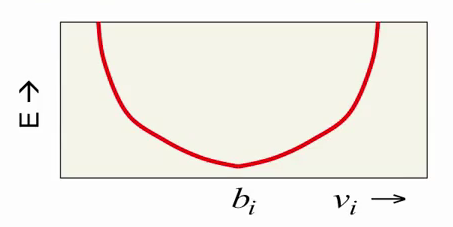
V iで RBMエネルギーがどのように変化するかを考えてください。 成分
b i (バイアス)は、i番目の可視ニューロンの望ましい値(対応する画像ピクセルの強度)に関与し、エネルギー自体はこの値からの偏差で2次関数的に増加します。
式の最後のコンポーネントは、
v iと
h iの両方に依存し、それらの相互作用を表し、
v iに線形に依存します。
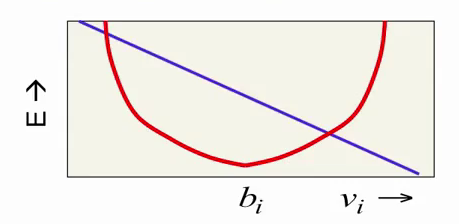
赤い放物線をまとめると、このコンポーネントはエネルギー最小値をある方向または別の方向にシフトします。 したがって、必要な動作が得られます。赤い放物線はニューロンに特定の値から強い距離を与えることでニューロンの値を制限しようとし、紫色の線はRBMの潜在状態に応じてこの値をシフトします。
ただし、ここで問題が発生します。 まず、目に見えるニューロンごとに、トレーニングの結果として適切なパラメーター
σiを選択する必要があります。 第二に、
σiの小さな値自体が学習困難を引き起こし、目に見えるニューロンが隠れに強い影響を与え、隠れたニューロンが目に見える影響を弱くします。
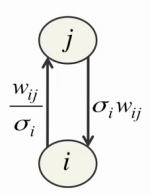
第三に、可視ニューロンの値が無限に増加する可能性があり、エネルギーが無限に低下するため、学習の安定性が大幅に低下します。 最初の2つの問題を解決するために、
Jeffrey Hintonは、トレーニング前にすべてのトレーニングデータを正規化し、期待値と単位分散がゼロになるよう提案し、上記の方程式のパラメーター
σiを1に設定します
[4] 。 さらに、このアプローチにより、通常の場合(バイナリニューロンのみを使用)と同じ
CD-nメソッドを使用して、統計の収集とRBMのトレーニングにまったく同じ式を使用できます。 3番目の問題は、学習率を1〜2桁減らすだけで解決されます。
...そしてさらに良い
その結果、限られたボルツマンマシンの可視ニューロンで実数値データを適切に表現することを学びましたが、内部の潜在状態はまだバイナリです。 隠されたニューロンを何らかの方法で改善し、より多くの情報を伝達することは可能ですか? それはあなたができることが判明しました。 隠れニューロンをバイナリのままにして、1より大きい自然数を表示するのは非常に簡単です。これを行うには、隠れニューロンを1つ取得し、可視ニューロン(重み共有)と訓練されたバイアス
biからまったく同じ重みでそのコピーを多数作成します確率を計算するとき、各ニューロンの変位から固定値を減算し、変位
b i -0.5、
b i -1.5、
b i -2.5、
b i -3.5のその他の点では同一のニューロンを取得します...その結果、
整流線形単位の整数バージョンを取得します分散
σ(x)のノイズを追加することにより
=(1 + exp(-x)) -1 (ニューロンの確率的性質のため)。 簡単に言えば、そのようなニューロンの入力で値
x = b i + ∑v j w i、jが大きいほど、そのコピーが同時にアクティブ化され、アクティブ化されたすべてのコピーの数が自然数として表示されます。
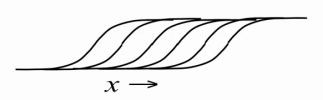
ただし、実際には、各ニューロンに多数のコピーを作成すると、RBMトレーニング/作業の各反復でシグモイド関数の計算回数が同じ回数だけ増えるため、費用がかかります。 したがって、私たちは劇的に行動します-すぐに各ニューロンに無限のコピーを作成します! これで、1つの単純な式
[1,5]を使用して、各ニューロンの結果値を計算できる単純な近似ができました。
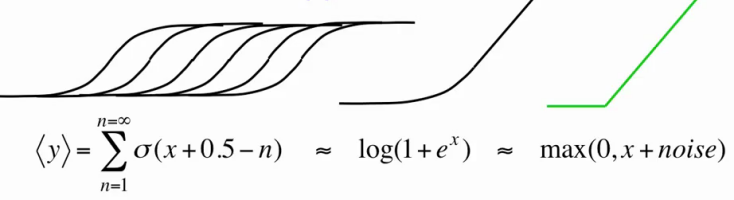
このように、隠れたニューロンは、ガウスノイズを含むバイナリから修正された線形ユニットに変わりましたが、学習アルゴリズムはそのままでした(結局、これらは実際には同じバイナリニューロンであり、上記のコピー数は無限であると仮定しています)。 これで、0と1だけでなく、自然だけでなく、すべての非負の実数を表すことができます! 分散
σ(x) ∊ [0; 1]は、完全に非アクティブなニューロンがノイズを生成せず、
xが増加してもノイズが非常に大きくならないようにします。 さらに、素晴らしいボーナス:何らかの理由でデータの予備的な正規化が不可能または望ましくない場合、そのようなニューロンを使用すると、各ニューロンのパラメーター
σiを学習することができます
[1,2]が 、これについては詳しく説明しません。
トレーニングの実施
正規分布式から期待値を削除すると、可視ニューロンの値は式によって計算できます

ここで、
N(μ、σ2)は、正規分布、期待値μ、および分散σ2を持つランダム変数です。
[4,5]のジェフリーヒントンは、トレーニング中の可視ニューロンの再構築にガウスノイズを使用しないことを提案しています。 0または1を選択する代わりにバイナリニューロンの場合に純粋な確率を使用するのと同様に、これはノイズを減らし、アルゴリズムの1ステップの実行時間を少し短くすることで学習を高速化します(各ニューロンに対して
N(0,1)を考慮する必要はありません)。 ヒントンのアドバイスに従って、完全に線形の可視ニューロンが得られます。
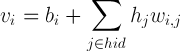
隠されたニューロンの値は、式によって計算されます

トレーニング自体を実装するには、CD-nの通常のバイナリニューロンとまったく同じ式を使用します。
実験
実験として、単に顔や手書きの文字を認識するよりも面白いものを選択します。 たとえば、人の顔にどんな感情が表れているのかを認識します。 データベースの画像のトレーニングとテストに使用します
Cohn-Kanade AU-Coded Facial Expression Database(CK +) 、
イェールフェイスデータベース 、
インディアンフェイスデータベース 、
日本女性の表情(JAFFE)データベース 。
すべてのベースのうち、特定の感情(8つのうち1つ:中立的な表現、怒り、恐怖、嫌悪、喜び、驚き、軽、悲しみ)でマークされた画像のみを選択します。 719個の画像を取得します。 ランダムに選択された画像の70%(500個)をトレーニングとして使用し、残りの30%(219個)を検証データとして使用します(この例では、ヘルプでパラメーターを選択しないため、テスト画像として使用できます) 。 実装には、MATLAB 2012bを使用します。 各画像で、標準のvision.CascadeObjectDetectorを使用して顔を選択し、結果の正方形の領域を10%拡大して、顎が処理された画像に完全に収まるようにします。 結果の顔の画像を70x64のサイズに圧縮し、グレーの濃淡に変換し、ヒストグラムの均等化を適用して、すべての画像のコントラストを均等にします。 その後、各画像を1x4480ベクトルに展開し、対応するベクトルをtrain_xおよびval_x行列に保存します。 train_yおよびval_y行列には、対応する目的の分類器出力ベクトル(サイズ1x8、入力ベクトルによって表される感情の位置に1、残りの位置に0)を格納します。 データの準備ができたら、実験を開始します。
分類子を実装するには、既存の
DeepLearnToolboxソリューションを選択し、フォークし、必要な機能を追加し、バグ、欠点、
ヒントンガイドとの矛盾を修正し、
新しいDeepLearnToolboxを取得します。
ニューラルネットワークの各層のニューロン数:4480-200-300-500-8.隠れ層のこのような少数のニューロンは、数が少ないため、すべての入力画像の過剰適合と単純なネットワーク記憶を排除するために選択されます。 まず、シグモイド活性化関数を使用してニューラルネットワークをトレーニングし、事前トレーニングに通常のバイナリRBMを使用します。
tx = double(train_x)/255; ty = double(train_y); vx = double(val_x)/255; vy = double(val_y);
ニューラルネットワークのトレーニングスケジュール:
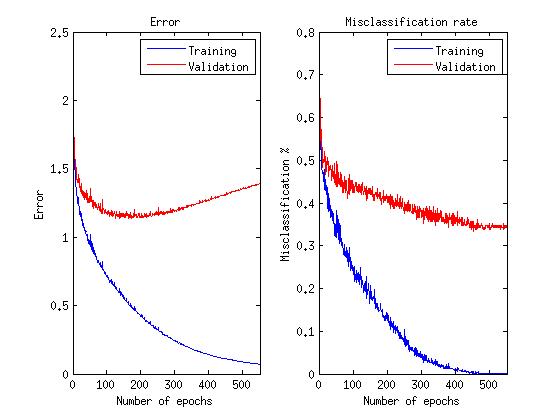
10の検証データの平均誤差は、トレーニングデータと検証データの新しいランダムサンプルが36.26%になるたびに始まります。
次に、修正された線形活性化関数を使用してニューラルネットワークをトレーニングします。事前トレーニングには、説明したRBMを使用します。
tx = double(train_x)/255; ty = double(train_y); normMean = mean(tx); normStd = std(tx); vx = double(val_x)/255; vy = double(val_y); tx = normalize(tx, normMean, normStd);
ニューラルネットワークのトレーニングスケジュール:
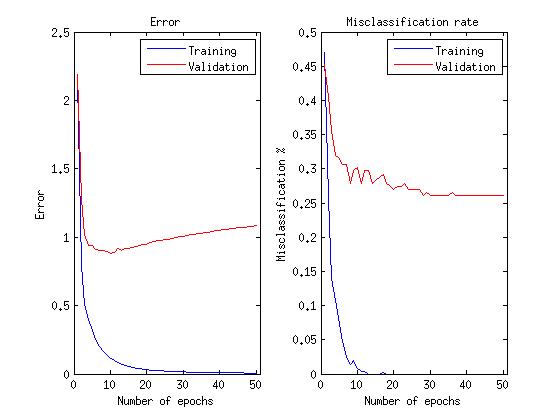
バイナリニューロンの場合と同じサンプルで開始した10個の検証データの平均誤差は28.40%でした
グラフに関する注意:私たちは実際にネットワークが感情を正しく認識し、エラー関数を最小化しないことに関心があるため、エラー関数が成長し始めても、この能力が改善するまでトレーニングを続けます。
ご覧のように、限定されたボルツマンマシンで線形および修正線形ニューロンを使用すると、認識エラーを8%削減できました。その後のニューラルネットワークのトレーニングでは、反復(エポック)が10倍少なくなったという事実は言うまでもありません。
参照資料
1.
機械学習のためのニューラルネットワーク(ビデオコース)2.
Gaussian-Binary Restricted Boltzmann Machinesによる自然画像統計の学習3.
小さな画像から複数のレイヤーの特徴を学習する4.
制限付きボルツマンマシンのトレーニングの実践ガイド5.
直線化された線形ユニットが制限付きボルツマンマシンを改善