空間検索の必要性は頻繁に発生します。 空間のJOIN'eと同様に、2セットのフィーチャの交差を見つけます。 常に重砲を引き付けたいとは限りません。 さて、「小さな血、強烈な打撃」で問題を解決する方法を考えてみましょう。
はじめに
1次元以上のオブジェクトのインデックス作成は重大な問題であることが知られていますが、この必要性は非常に大きいです。 生じる困難は本質的に客観的です。 何をするにしても、物理メディア上のインデックスファイルはシーケンシャル(1次元)であり、プレーン(スペース)の何らかのトラバーサルを提供する必要があります。 同時に、インデックスファイル内の非常に遠くないスペースにポイントを配置する直感的な要望があります。 残念ながら、休憩なしではこれは不可能です。
GISコミュニティでの空間インデックス作成に対する態度は、一般に2つあります。 一方で、このコミュニティのかなりの数のメンバーは、まったく問題がないと確信しており、そのような必要性が生じた場合、彼らは2つの方法でそれを処理したでしょう。 一方、「すべてが私たちの前に盗まれた」という意見もあります。最新のDBMSのほとんどは、この問題をなんとかして解決することができます。
よくあることですが、gopherが表示されないという事実は、gopherが存在しないという意味ではありません。 データ量が大幅に増加すると、空間インデックスの構築自体が問題になる可能性があります。 アルゴリズムが定義を超えるか、構築時間が許容できないほど長くなるか、検索が無効になります...空間データが急速に変化し始めるとすぐに、空間インデックスが低下し始める可能性があります。 インデックスの再構築は役立ちますが、長くは続きません。
ここでは、空間データのインデックス作成の最も単純なケース、つまりポイントフィーチャの操作について見ていきます。 掃引曲線を使用した座標の正直なコーディングを使用します。 もちろん、ピクセルブロックインデックス、Rツリー、クアッドツリーなど、他の方法もあります。 おそらくこれは別の記事のトピックかもしれませんが、今度はスイープカーブの助けを借りてポイントオブジェクトを使用した作業を正確に説明しています。
提案された方法が理想的であるとは言いませんが、少なくとも2つの利点があります-それは非常にシンプルで非常に効果的です。 その助けにより、文字通り「膝の上」で、あなたは非常に深刻な問題を解決することができます。
データとして、スターアトラスとその乱数によるシミュレーションを使用します。 各データセットはいくつかのオブジェクトで構成されており、それぞれについて説明します。
- X-座標、32ビット整数値
- Y-座標、32ビット整数値
- VAL-32ビット整数値
試験データ
いくつかのデータセットがあります。
- 55M-このセットは、座標が間隔0 ... 2 ** 27の乱数およびXの0 ... 2 ** 26の乱数である55,368,239個のオブジェクトで構成され、VALは常に0です。
- 526M-このセットは、座標が間隔0 ... 2 ** 27の乱数およびXの0 ... 2 ** 27の乱数である526,280,881オブジェクトで構成され、VALは常に0です。
- USNO-SA2.0-これは、ftp://ftp.nofs.navy.milから取得した55.368.239スターのカタログです。
X座標は、10進数の時間でのRA(右アセンション)* 15 * 3600 * 100です。
Y-座標-((10進数のDEC)+90)* 3600 * 100
VALは特定の値で、特に赤と青の範囲の明るさを含みます。
- USNO-A2.0-これは526,280,881個の星のカタログで、ftp://ftp.nofs.navy.milから入手できます。 このデータの推定値のみが提供されます。 オブジェクトの値はUSNO-SA2.0に似ています
理論
掃引曲線の考え方は、離散空間に番号を付けることです。 フィーチャは、N次元空間のポイントで表されます。 平面上の点はそれ自体を表し、平面図を表す長方形の範囲は4次元の点などです。 このようなポイントは、処理が非常に簡単な固定長の数値です。 特に、そのような番号は通常のBツリーに配置できます。 検索クエリは、スイープ曲線の連続セグメントに分割され、各セグメントに対してサブクエリが実行されます。 サブクエリ間隔に該当するすべてのポイントが必要なものです。
したがって、(この場合は2次元の)離散空間のすべての点を訪れる曲線が必要です。 オプションは何ですか?
- イグルー。 2次元空間には、画像管のスキャンのように、行ごとに番号が付けられます。 2次元空間に均一に分散されたポイントオブジェクトと小さなクエリの場合、この方法は理想的です。 その欠点は次のとおりです。
- 2次元空間で効果的に機能します。それ以外の場合は、多数のサブクエリが生成されます。
- 大きな検索範囲の場合、多数のサブクエリが生成されます。
- 傾向のあるデータのクラスタリングには非効率的
- 自己相似曲線。 掃引曲線は本質的にフラクタルであり、単位セル(たとえば、2x2の正方形)には特定の方法で番号が付けられ、その後、各サブセルにも同様の方法で番号が付けられます。 最も有名なそのような曲線は、いわゆるZオーダー(またはビットインターリーブ)であり、その性質は名前に由来します。 64x64の解像度で平面に番号を付けると、次のようになります。
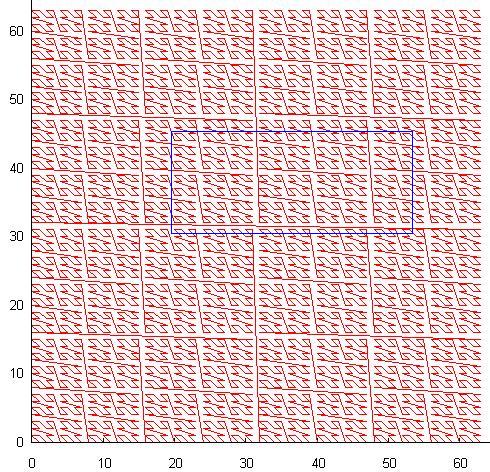
図の青い長方形は典型的な検索クエリであり、曲線を横切るたびに新しいサブクエリが生成されます。 実際、不注意に使用すると、このメソッドはイグルーよりも多くのサブクエリを生成します。 これは、このメソッドがDBMSで実際に使用されないという事実を説明しています。 ただし、類似性自体が、不均等に分散されたデータへの適応という素晴らしい機能を備えています。 さらに、曲線の連続したセグメントは、スペースの重要な領域をカバーできるため、使用できる場合に便利です。
- 別のオプションは、自己相似曲線:ヒルベルトU字曲線です:
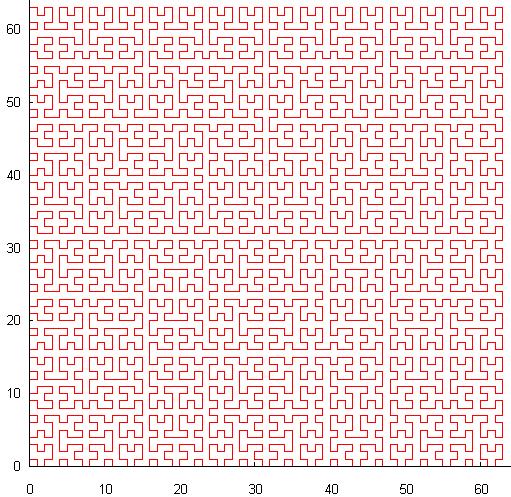
Zオーダーとは異なり、この曲線には連続性があり、これにより検索がより効率的になります。重大な欠点は、値から座標を計算するコストが比較的高いことです。
2X2の自己相似性を持つ3番目のオプション:X字曲線はそれ自体と交差し、作成者は空間インデックス付けの使用の先例を知りません。
ヒルベルト曲線、 シェルピンスキー曲線、 ゴスパー曲線の類似物であるムーア曲線も知られています...
- いわゆる カスケードイグルー:
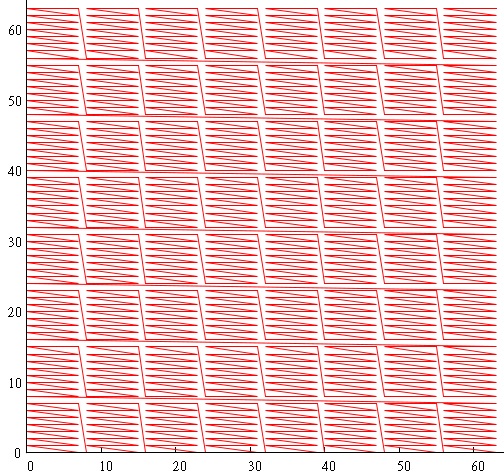
この画像を取得するために、座標範囲を3ビットの断片に分割し、XとYを混合しました。 掃引曲線の値は次のように取得されます。
- ビット0〜3はビット0〜3のX座標です
- ビット3〜6はY座標のビット0〜3です。
- ビット6〜9はビット3〜6のX座標です。
- ビット9〜12は、Y座標のビット3〜6です。
したがって、内部に水平スキャンを備えた8X8ブロックを取得し、それ自体が水平スキャンを形成します。
しかし、これは原理を実証するためです。 インデックス作成のために、17ビットのブロックを作成します。 理由17に興味がある場合は、後で詳しく説明します。
結果
インデックス作成
| データセット | ディスクサイズ(Kb) | ビルド時間 | MEMサイズ(Mb) |
|---|
| 5,500万 | 211,250 | 6'45 '' | 40 |
|---|
| 526M | 1,767,152 | 125 ' | 85 |
|---|
| USNO-SA2.0 | 376,368 | 4'38 '' | 40 |
|---|
| USNO-A2.0 | 3,150,000 | 125 ' | 85 |
|---|
どこで:
- ディスクサイズ-結果のインデックスファイルのサイズ(キロバイト単位)
- ビルド時間-作成にかかった時間(分/秒)
- MEMサイズ-インデックスビルダーに必要なMB単位のRAMのピークサイズ
インデックス検索
次の表に、構築されたインデックスのクエリに固有の値を示します。 ランダムに選択された(もちろん、居住地域で)正方形の範囲の100,000件の検索の合計値が表示されます。
- 5,500万
| 範囲サイズ | 時間(秒) | Nobj | RDisk | σ(RDisk) |
|---|
| 2x2 | 58 | 23 | 118,435 | 0.39 |
| 4x4 | 59 | 100 | 118,555 | 0.39 |
| 10x10 | 59 | 600 | 118,918 | 0.4 |
| 20x20 | 60 | 2,622 | 119,221 | 0.4 |
| 120x120 | 62 | 89,032 | 123,575 | 0.45 |
| 1200x1200 | 98 | 8,850,098 | 174,846 | 0.82 |
| 7200x7200 | 408 | 318,664,063 | 567,137 | 1.3 |
どこで:
- エクステントサイズ-検索エクステントのサイズ。USNO-SA(X).0の場合の単位は1アーク秒
- 時間-100,000リクエストに費やされた秒単位の時間
- NObj-すべてのリクエストで見つかったオブジェクトの数
- RDisk-ディスク読み取り操作の総数(内部キャッシュによるミス)。この値は、 サイズが数百メガバイトのファイルであっても、オペレーティングシステムによって効果的にキャッシュされます。
- σ(RDisk)はディスク操作数の標準偏差です。実験の結果によると、RDiskの最悪値は平均(RDisk)+ 12 *σ(RDisk)を超えていません。
- 526M
| 範囲サイズ | 時間(秒) | Nobj | RDisk |
|---|
| 2x2 | 738 | 110 | 185,672 |
| 4x4 | 741 | 445 | 185,734 |
| 10x10 | 730 | 2,903 | 186,560 |
| 20x20 | 774 | 11,615 | 187,190 |
| 120x120 | 800 | 421,264 | 196,080 |
| 1200x1200 | 1200 | 42,064,224 | 307,904 |
| 7200x7200 | 3599 | 1,514,471,480 | 1,442,489 |
スピーカーが55Mに似ている場合。
ディスクアクセスの数がわずかに(3分の1)変化した一方で、クエリの実行時間が10倍以上増加したことは注目に値します。これは、オペレーティングシステムによるインデックスファイルの効率的なキャッシングの欠如の結果です。
- USNO-SA2.0
| 範囲サイズ | 時間(秒) | Nobj | RDisk | σ(RDisk) |
|---|
| 2x2 | 48 | 28 | 143,582 | 0.5 |
| 4x4 | 50 | 115 | 143,887 | 0.5 |
| 10x10 | 45 | 657 | 144,085 | 0.5 |
| 20x20 | 45 | 2,585 | 144,748 | 0.51 |
| 120x120 | 47 | 94,963 | 151,223 | 0.56 |
| 1200x1200 | 80 | 9,506,746 | 224,016 | 0.97 |
| 7200x7200 | 387 | 345,165,845 | 842,853 | 2.97 |
スピーカーが55Mに似ている場合
- USNO-A2.0(グレード)
| 範囲サイズ | 時間(秒) | Nobj | RDisk | σ(RDisk) |
|---|
| 2x2 | 〜600 | 〜130 | 〜200,200 | 〜0.4 |
| 4x4 | 〜600 | 〜500 | 〜200,200 | 〜0.4 |
| 10x10 | 〜600 | 〜3,000 | 〜200,200 | 〜0.4 |
| 20x20 | 〜600 | 〜12,000 | 〜200,200 | 〜0.4 |
| 120x120 | 〜600 | 〜450,000 | 〜250,200 | 〜0.5 |
| 1200x1200 | 〜1,000 | 〜45,000,000 | 〜300,200 | 〜1.4 |
| 7200x7200 | 〜3500 | 〜1,600,000,000 | 〜1,500,200 | 〜2.0 |
スピーカーが似ているところ526M
空間結合
次の表に、結合インデックスに固有の値を示します。 結合とは、一定の範囲内にあるすべてのオブジェクトの検索を意味します。 たとえば、クエリパラメータが0.25アーク秒の場合、1つのインデックスの各要素に対して、範囲が+-0.25の2番目のインデックスで検索が実行されます。 辺が0.5x0.5アーク秒で、基準点を中心とする正方形。
- USNO-SA2.0対USNO-SA2.0
| 範囲サイズ | 時間(秒) | Nobj |
|---|
| 0.5x0.5 | 175 | 2 |
| 2x2 | 191 | 410 |
| 6x6 | 212 | 4,412 |
どこで:
- エクステントサイズ-アーク秒単位の検索範囲
- 時間(秒)-クエリ実行時間(秒)
- NObj-見つかったオブジェクトの数(自身を含まない)。この場合、半分に分割する必要があります。 これは自動参加です
- 55M対USNO-SA2.0
| 範囲サイズ | 時間(秒) | Nobj |
|---|
| 0.5x0.5 | 150 | 925 |
| 2x2 | 165 | 13,815 |
| 6x6 | 181 | 122,295 |
列がUSNO-SA2.0とUSNO-SA2.0に類似している場合。
- 526M対526M
| 範囲サイズ | 時間(秒) | Nobj |
|---|
| 0.5x0.5 | 1601 | 0 |
| 2x2 | 1813 | 916 |
| 6x6 | 2180 | 9943 |
列がUSNO-SA2.0とUSNO-SA2.0に類似している場合。
どのように、なぜ機能するのですか?
まず、重要な点に注意してください。
- 大きなファイルの場合、ディスクキャッシュは機能しません。依存しないでください。
- 要求の処理時間は主にディスクの読み取り時間で構成され、他のすべての時間は比較的小さくなります。
- ランダムに分散されたクエリの場合、キャッシュは機能しません。インデックスがBツリーとして配置されている場合、ページキャッシュに依存して過度のメモリを浪費しないでください。
- 空間的に近いクエリの場合、小さな(数十ページ)キャッシュで十分です。
それでは、データの配置方法を理解してみましょう。
- グローバル範囲-2 ** 26 X 2 ** 27または180X360度。
- 180度は180 * 60 * 60 = 648000アーク秒です。
- 1 << 26 = 67 108864。したがって、1角秒は〜100サンプルです。
- 1つのオブジェクトは、平均1600 =(2 * 648000 * 648000/500000000)平方秒〜(40X40)を占めます。
- または40 * 100 = 4000サンプル。
- 〜1000個のオブジェクトがBツリーページに配置されます。
- ツリーページをカスケードイグルーブロックに対応させたい場合、このブロックを4000 * sqrt(1000)=>〜1 << 17のサイズにします
- それがマジックナンバー17です。
- そのため、平均ページにはエクステント(40 * 32)〜1200X1200アーク秒があります。
- データでは、このようなページは、カスケード接続されたイグルーの2つの隣接するブロックに物理的に配置されている可能性が高い
- したがって、角度が最大600X600秒の検索クエリでは、シートページの読み取りが1回だけ必要になる可能性があります。
- 4レベルのインデックスツリーと上位2レベルが効果的にキャッシュされることを考えると、このサイズの平均クエリにはディスクからの2つの物理読み取りが必要です。
- 説明するために必要でした。
それでは、検索はどのようにすべて同じですか?
- ブロックインデックスデバイスに従って、検索範囲を分割します。
- エクステントの各部分は1つのインデックスブロックに対応し、独立して処理されます。
- ブロック内で検索範囲の境界線を見つけます
- 範囲全体を減算し、検索範囲外のすべてを除外します。
少し残念ですが、それはいかに簡単か。
まとめ
- 私たちが知っている最大の機能アトラス(約3,000,000,000)でも、数時間でインデックスを作成できます。
- このようなインデックスを格納するために必要なディスクメモリの量は、数十(〜30)ギガバイト単位で測定され、オブジェクトの数はほぼ線形です。
- 検索に必要なRAMの量は非常に少なく(Mb単位)、組み込みシステムを含め、インデックスを使用できます。
- 小さい範囲(オブジェクト間の平均距離に匹敵するサイズ)による空間検索の場合、この場合の検索時間は2〜3回のディスク操作の時間に近づきます。 ほぼ物理的な限界に
- 比較的大きなクエリの場合、検索時間は選択内のオブジェクトの数により依存します
- いずれにせよ、時間は予測可能なままであるため、リアルタイムシステムを含め、このインデックスを使用できます。
PS
説明された作業は、著名な会社
DataEastの Alexander Artyushinと共同で2004年に実施され
ました 。 当時、著者自身がこの会社の従業員であり、はい、Evgeny Moiseev
emoiseevのおかげで、彼らの同意を得て出版が行われています。
当時の鉄は現在に匹敵するものではありませんでしたが、基本的なポイントは変わっていません。