パート2では 、Hindley-Milnerアルゴリズムに関する
StackOverflowの質問で見ることができるすべての正式な用語と記号の定義になりました。 これで、そこで求められていること、つまり型推論に関するステートメントを導出するためのルールを翻訳する準備ができました。 さあ始めましょう!
型推論ステートメントを導出するためのルール
[Var]
これは次のように変換されます。「
xがタイプσである」が位置Γのコレクションからの位置である場合、Γから
xがタイプσであると推定できます。 ここで、
xは変数です(ルールの名前です)。 はい、痛いほど明らかですが、機械が理解できる簡潔で簡潔な形式の深く複雑な事実が含まれています。 これにより、型推論を自動化できます。
[アプリ]
これは次のように変換されます:
e 0が
τ →
τ ′型の式であると推定できる場合(つまり、
e 0は匿名関数で、Γに従って入力として
τ型の値を取り、型の値を返します
τ )であり、
e 1が
τ型である場合、
e 0 (
e 1 )
e 0を
e 1に適用して得られる式は
τ '型であると結論付けることができます。 直感的なポイント:関数の入力と出力のタイプ、および一部の式が入力と同じタイプを持っているという事実を推測できる場合、この式に関数を適用すると、結果が安全であると結論付けることができます式には関数出力のタイプがあります。 ここで混乱するものはありません。
[腹筋]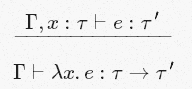
これは次のように変換されます:
xがタイプ
τであり、
eがタイプ
τ ′であると仮定できる場合、変数
x -
λx.eに関して
e抽象化/匿名化のタイプも推定できると結論付けることができます。
τ →
τ ′になります。 つまり、たとえば、型
xが
Stringであることがわかっている場合、式
x[0]は
Char型になります。 [Abs]により、次のように結論付けることができます。
function(x) { return x[0]; }
タイプは
String →
Charです。
側に。 ポリタイプについてはすでに言及しました。 この概念を私の頭により良くフィットさせるために、この例でそれらに戻りましょう。 そのため、上記の関数は
Array[Int] →
Int型であることにすでに気付いています。 実際、型
t関数は
Array[t] →
tです。 そのため、実際には多くの異なるタイプがあり、
String →
Charはそのうちの1つにすぎません。
Array[t] →
t形式の
各タイプはモノタイプです。 この関数はポリタイプtype
t(Array[t] →
t)持っていると言うだけで、これらのモノタイプを
すべて持っていると推測できます。 「任意の
t -型は
Array[t] →
t 」であり、すべての束を単一の型で表します(ただし、より抽象的です)。 したがって、式の型を推測するとき、これがこの式の唯一の型であることを意味しないことに注意してください。 それは多くの異なるタイプを持つことができ、そのうちのいくつかはより専門化され、他のものはより抽象的になります。 タイプの最も単純なタイプはモノタイプです:
Int 、
String 、
String →
Charなど。ただし、必要に応じて、より抽象的な/一般的なタイプ-ポリタイプを作成できます。
[ましょう]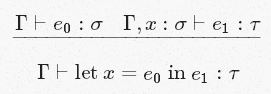
一般的に簡単:
e 0がσ型であると推定できる場合
そして
xもタイプσがあると仮定すると、これから
e 1がタイプ
τであると推定できます。
それから
xを
e 0に等しく設定し、それを
e 1に代入した結果は
τ型になると結論付けることができます。
最後の4つのルールは、匿名関数を作成したり、通常の関数を適用したり、式内の式を置換したりする変数がある場合に取得できる型に関する直感的な知識の形式的な反映にすぎません。 これは、プログラマとして私たちが直感的に行うことです。 ここでは、これらすべてを正式に説明する方法について説明します。 結局、私たちの脳で起こるすべてが未知の魔法というわけではありません。 最後の4つのルールは、ラムダ計算で有効な式を決定する4つのルールに正確に対応していることにも注意してください。 これは偶然ではありません。
[Inst]
これはインスタンスルールです。 モノタイプの
Array[Int] →
Intは、ポリタイプ
t.Array[t] →
tインスタンスと考えることができます。 つまり、これは「特殊化」です。
Array[Int] →
Int 、
t.Array[t] →
tよりも特殊化されています。 specializedによる「より専門的な」という意味です。 つまり

したがって、[Inst]の直接変換は次のとおりです
eがσ ′型であり、σがσ′のインスタンス/特殊化であると推定できる場合、
eはσ型であると結論付けることができます。 σとσ ′は、それぞれ
Array[t] →
tと
t.Array[t] →
tと考えることができます。
[Gen]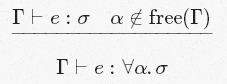
これは理解するのが最も難しい部分です。 本当に、上で概説した狭いルールのセットを使用する型推論プロセスのコンテキストでは、それだけが重要です。 型変数の概念に大きく依存しているため、明確な類似性はありません-実際のプログラミング言語には決して見られないものですが、メタ言語を使って任意の任意の型について話すときは不可欠ですプログラミング言語。 一般的に、アイデアは次の「例」に示すことができます。
2つの変数
xと
yがあり、最初に両方がタイプαであると仮定します。ここで、αはタイプを示す変数です。 後で、
このコンテキスト(
xと
yがタイプαであるという仮定のコンテキスト)で、そのタイプがα→αであると何らかの形で推定された式に出くわします。 そして今、注意が問題です:この関数はポリタイプ∀α.α→αを持ちますか? つまり この関数は、一般にオブジェクトを同じ型に関連付けますか、それとも
xと
yが同じ型αであると仮定したために、このように見えるだけですか
αは型変数、つまり 任意のタイプを表すことができますが、
eがタイプα→αであると推定したため、ポリタイプ∀α.α→αも持つと考えたいと思います。 しかし、
eが
xと
yにどのように関係しているかをより完全に理解しない限り、この一般化が必要だとは言えません。 特に、タイプα→αであるという結論が、このタイプに関連する以前の仮定と強く結びついている場合、
eがポリタイプ∀α.α→αであると結論付けることはできません。
そして今(最終的に!)ルールの翻訳:
タイプαの変数が現在のコンテキスト/知識のセット/仮定で「自由に」言及されておらず、式
eにタイプσがあると推定できる場合、
eに関係なく、タイプσがあると結論付けることができます。 、最終的にαになるもの。 もう少し技術的に:
eにはポリタイプ∀α.σがあります。
さて、しかし「ゆるやかに言及」とはどういう意味ですか? ポリタイプ∀α.α→α、αは、「本当の」とは呼ばれていません。 このタイプは完全に類似しています。たとえば、∀β.β→βです。 これらのタイプのいずれかを持つ式は、同じ入力タイプと出力タイプを持つ通常の関数です。 一方、
x: αは、αの「実際の」言及です。
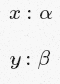
そして
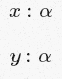
別のことを意味します。 後者は、
xと
y間違いなく同じ型であることを示唆しています(その型がまだ定義されていない場合でも)。 最初のものは、タイプ
xと
y関係をまったく報告しません。 違いは、αがドメインinside内で言及される場合(∀α.α→αの場合のように)、残りのコンテキストに関係なく、他の型変数で置き換えることができる単なるフィクションであるということです。 したがって、「αはΓの文脈で自由に言及されていない」という位置を「まったく言及されていないか、フィクションと見なされており、原則として、文脈の知識/仮定の意味を変更することなく完全に異なるものに置き換えることができます」と解釈できます。
以上です。
翻訳者のメモ:翻訳に関するPMのコメントに非常に感謝します。