
それぞれが
100 km / hの速度で移動する2台の同一の車が正面衝突します。 これは、
200 km / hの速度でのコンクリートの壁との衝突に相当しますか?
100 km / hの速度で
完全に回復力のあるサイクリストが重い列車と正面衝突し、
100 km / hの速度で移動します。 サイクリストは時速
300 kmで跳ね返りますか?
あなたが質問に「
いいえ、はい 」と答えたなら、あなたは正しいです、そして、私はあなたに何も新しいことを話しません。 そして残りは猫に誘います。 そこには
so弁はありません。
2台の車の衝突
実際、
100 km / hの速度での同一車の正面衝突は、
100 km / hの速度での重い壁との衝突に相当します。 それを理解してみましょう。
これら2台のマシンの重心を考えてみましょう。これらのマシンのちょうど真ん中にあります。 衝突中、この中心は移動しません。 さらに、車が完全に弾力性があるか、絶対に弾力性がないか、本物かは関係ありません。 したがって、この時点で仮想壁を配置できます。 また、2台のマシンのそれぞれがシステムの総エネルギーの半分を吸収することに注意してください。 まったく同じエネルギー(
mV 2/2 )が、同じ速度で壁に飛び込む車に吸収されます。
したがって、この衝突を
200 km / hの衝突と比較することは不適切です。
サイクリストと列車の衝突
絶対に回復力のあるサイクリストが時速
300 kmで列車から跳ね返ることを示します。
絶対的な弾力性は、サイクリストがすべてのエネルギーと速度を失い、ケーキにならないようにし、列車のフロントガラスをさらに移動できるようにします。

サイクリストの速度を
v 、列車の速度を
Wとしましょう
。 速度はスカラーです(図1)。
- 始めるために、列車参照システムに移りましょう。 速度の加算に関する定理により、静止物体に変わりますが、自転車の速度は増加し、 v + Wに等しくなります (図2)
- 衝突は絶対に弾力性があるため、サイクリストは同じ速度v + Wで跳ねます (図3)
- 静止観測者の基準枠に戻ります。 すべてのオブジェクトは、左に速くWに移動し始めます。 列車は再び行き、サイクリストの速度はv + 2Wに増加します(図4)
- そして、この例ではv = W = 100 km / hなので、サイクリストの速度は300 km / hに等しくなります
同様の推論、運動量とエネルギーの保存の法則を考慮
して、弾性衝突における速度の公式が導き出されます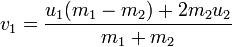
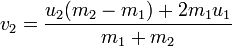
ここで、
u iは衝突前の速度、
v iは後、
m iは質量です。 速度ベクトル。
m 2を無限に移動すると、同じ結果が得られます(異なる方向に
u 1と
u 2が
あることを忘れないでください)。
おわりに
このタスクがHabrの訪問者にとってささいなものではないことを願っています。私の推論はあなたに明らかでした。 さもなければ、私は激怒する危険を冒します。 いずれの項目にも同意しない場合、または明確でない場合は、コメントに項目番号を記載してください。
良い金曜日を。