すべてのタスクとYandex.Algorithmの結果の分析

ほんの数時間前、オープンプログラミングチャンピオンシップYandex.Algorithm 2013はサンクトペテルブルクで終了しました。 競争は、各100分のオンラインラウンドで構成され、84か国の3,000人を超えるプログラマーが勝利を目指して戦いました。 3回の予選ラウンドの結果によると、上位25位が決勝に達しました。



ファイナリストは、6つのアルゴリズムの問​​題を100分で解決する必要がありました。 最初の場所は、NRU ITMO Gennady Korotkevich（ツーリスト）のチームでACM ICPC 2013の最近の勝者が撮影したもので、ペナルティタイムが最も短くなりました。 2位は、NRU ITMOのYevgeny Kapun卒業生です。 3位は、台湾の代表であるShi Bixunが獲得しました。

いくつかの国からの専門家が、選手権のタスクの準備に参加しました：ロシア、ベラルーシ、ポーランド、日本。 主なタスクコンパイラは、ヤンデックスミンスクオフィスの開発者でした（すべての会社の従業員と同様に、コンテストへの参加は許可されていませんでした）。 すべての著者に、Yandex.Algorithmの参加者のために準備したタスクを解析するように依頼しました。 ところで、誰もすべての問題を解決することはできませんでした。最良の結果-3つの解決された問題-は3人の参加者のみを示しました。

タスクA.カット！

問題と構文解析：ヤクブ・パチョッキ、ワルシャワ大学

入力ファイル名 ：stdin
出力ファイル名 ：stdout
制限時間 ：8秒
メモリ制限 ：512 MB

通常、チームプログラミングコンペティションでは、大学の正式名称に加えて、略称が与えられます。 ある非常に権威のある競技会では、チームは2つのチームのうち、辞書編集的に最小の略称を持つチームがビュッフェの近くに座るように座ります。 これを念頭に置いて、各大学のトレーナーは結果が辞書編集的に最小限になるように大学の名前を短くしようと努力しています。

大学名の空でない部分文字列を単語として指定します。これは文字で構成され、この部分文字列の直前の記号も直後の記号も文字ではありません。 大学名の略語が単語の接尾辞をドット記号（ "。"）で置き換えることが許可されている場合。

この場合：

• 単語全体をピリオドに置き換えることは許可されていません
• 単語が変更されていない場合（つまり、空の接尾辞が選択されている場合）、ドットは設定されません。

一般的に大学の名前を短くしないで、そのままにしておくことは許可されています。
名前を比較すると、すべての非ラテン文字が削除され、すべての大文字のラテン文字が対応する小文字に置き換えられ、結果の文字列が互いに比較されます。

入力ファイルの形式。 入力ファイルの最初の行には、大学の名前が含まれています。 名前には、大文字と小文字のラテン文字、スペース、コンマ（ "、"）およびハイフン（ "-"）を含めることができます。
行がスペースで始まり、スペースで終了せず、2つの連続したスペースが含まれないことが保証されます。 入力ファイルの文字数（スペースを含む）は10 ^6を超えません。

出力ファイル形式。 大学の辞書編集上最小の略称を印刷します。 元の名前と比較して、文字の大文字と非文字記号の位置を変更することは禁止されています。 辞書編集的に最小の場合
いくつかの略語、任意を印刷します。

標準	標準
ワルシャワ大学	ユニ Wの
サンクトペテルブルク国立研究大学、機械および光学	セイン。 Pe。 な リサーチユニ I、M、Oの
イリノイ大学アーバナシャンペーン校	ユニ I. of U.-C
、カーネギー-、-メロン-、-、--大学-	、Ca .--、-MelloN-、-、-U.-
ウドムルティアン大学	Udm。 U.

ご注意 「ユニ。 文字列「uniofw」は、他のバリエーションに対応する文字列よりも辞書式に小さいため、「W。of of」は「ワルシャワ大学」の辞書編集上最小の略語です。たとえば、「uow」、「uniofwa」、「universityofwarsaw」です。

問題Aの解決策

入力を解析した後、タスクは次のように要約されます。

合計長N の n行s ₁ 、... s _{nについて} 、 _次のような空でない接頭辞p ₁ 、...、 p _nを見つける

p ₁ p ₂ ... p _n

辞書編集的に最小です。

文字列p _{k + 1} p _{k + 2} ... p _nが辞書編集的に最小であるようなp _{k + 1} 、...、 p _nをすでに見つけたと仮定します。 このp _{k + 1} 、...、 p _nの選択は、 p ₁ 、...、 p _kの任意の選択に最適であることに注意してください。 これは、2つの文字列tとt 'でt < t'が真である場合、任意の行wで wt < wt 'であるという事実に基づいています。

与えられたp _{k + 1} 、....、 p _nから最適なプレフィックスp _kを効果的に見つける方法
t ：= p _{k + 1} p _{k + 2} ... p _{nを入力し}ます。 文字列ptが辞書的に最小限になるように、文字列s _kの空でない接頭辞pを見つける必要があります。

ハッシュを使用してpt 文字列とp't文字列を効果的に比較できるアルゴリズムがあります。

• バイナリ検索を使用して、行ptおよびp'tの最大共通プレフィックスを見つけます。
• このプレフィックスの直後の文字を比較します。

ランダム化されたハッシュを使用すると、アルゴリズムは（log N ）に対して非常に高い確率で機能します。
p _kを見つけるには、|を実行する必要があります。 s _k | -1 p _kを計算する時間（| s _k | log N ）を与えるそのような比較。 すべてのs _kを合計すると、アルゴリズムの実行時間（ N log N ）が得られます。

問題B. Anyutaと「ビット単位のAND」

問題と分析の著者は、アレクセイ・トルスティコフとローマ・ウドビチェンコです。
入力ファイル名 ：stdin
出力ファイル名 ：stdout
制限時間 ：2秒
メモリ制限 ：512 MB

Little Anyutaは、数値のビット演算を検討することにしました。 今日、彼女は「ビット単位AND」演算を研究しました。 ビット単位のANDは、オペランドのバイナリ表現の同じ位置にあるビットの各ペアに論理ANDを適用することと同じです（バイナリ表現では先行ゼロを使用できます）。 つまり、オペランドの対応するビットが両方とも1である場合、結果のバイナリビットは1です。 ペアの少なくとも1つのビットが0の場合、結果のバイナリビットは0です。

驚いたことに、ちょうど今日、Anyutaの両親は仕事から2組の数字を持ち込んだ。 お父さんは仕事からP番号で構成されるセットAを持ってきて、母はM番号で構成されるセットBを持ってきました。 セット内のすべての数値は、負ではなく、65535を超えない整数でした。さらに、セット内の番号には1から始まる番号が付けられていました。

うれしそうなアニーはすぐに、研究した操作をこれらのセットの数字に適用し始めました。 彼女の両親を怒らせないために、彼女はビットのAndをそれらの数字のペアに適用しました。そのうちの1つは私の父のセットのもので、もう1つは私の母のセットのものでした。

アニーはコンピューティングに情熱を傾けていましたが、彼女の両親は娘がXを獲得する方法はいくつあるのだろうかと考えました。 異なる方法の数は、1≤i≤P、1≤j≤M 、A _i AND B _j = Xとなるように、異なるペア（i、j）の数として計算できます。 Anyutaの両親は娘よりも好奇心が強いため、1つの数字Xだけでなく、すぐにKの数字X _iについて必要な数のウェイを見つけたいと考えています。 親を助けて！

入力ファイルの形式。 最初の行には、スペースで区切られた3つの整数P 、 M 、およびK （1≤P、 M 、K≤10 ⁵ ）が含まれています-それぞれ、父親のセットの数字の数、母親のセットの数字の数、および親が関心のある数字の数。 2行目には、スペースで区切られたP個の数字A _iが含まれています-お父さんが持ってきた数字のセット。 3行目には、スペースで区切られたM個の数字B _iが含まれています。ママが持ってきた数字のセットです。 4行目には、スペースで区切られたK個の数値X _iが含まれます。これは、必要なペアの数を計算する必要がある一連の数値です。 セットA 、 B 、およびXのすべての数値は整数で、負ではなく、65535を超えません。

出力ファイル形式。 それぞれ1つの数字を含むK行を印刷します。 i番目の行の数は、条件に記述された規則に従ってセットAとBからの数にビット単位のAND演算を適用することにより数X _iを取得する方法の数と等しくなければなりません。

例

標準	標準
4 4 4 1 2 3 4 1 2 3 4 1 2 3 4	3 3 1 1
1 2 3 0 1 2 0 1 2	2 0 0

問題Bの解決策

2 ¹⁶までの非負の整数で構成される2つの配列AとBが与えられます。 また、最大2 ¹⁶までの数値を含むQクエリの配列も提供されます。 各クエリkについて、 Ai AND Bj = Qkとなるようなペア（ i 、 j ）の数を指定する必要があります。

各配列の要素の数は最大100kです（ただし、2 ^16を超えないことがすぐにわかりますが、同じものを処理する必要があるため、最大100kの配列があります）。

すべてのリクエストについてすぐに回答を検討します。

以下の表記f （ x 、 S ）を導入します-xからのすべてのビットを含むシーケンスSからの要素のセットと、場合によってはそれ以上（つまり、 x ＆ y = xのような数値y ）。
a∈f （ x 、 A ）およびb∈f（ x 、 B ）の場合、 （ a ＆ b ）＆ x = x 、すなわち a ＆ bにはxと同じビットがすべて含まれますが、いくつかの追加ビットが含まれている可能性があります。

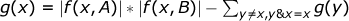
g （ x ）をA _i ＆ B _j = xとなるようなインデックスのペアの数（ i 、 j ）とすると、 。 したがって、インデックスの可能なすべてのペアから、 A _i ＆ B _j > xのペアを減算します。

Bを入力の数値の最大ビット数とします。 その後| f （ x 、 S ）| すべてのxについて時間O（| S | + 3 ^B ）で計算できます（ xのビットのすべてのサブセットを列挙する方法を使用）。 g （ x ）の値は時間O（3 ^B ）で計算できますが、この場合、ビットxのすべてのサブセットではなく、すべてのスーパーセットの列挙を使用する必要があります。

説明されているソリューションの合計動作時間はO（ P + M + K + 3 ^B ）（ B = 16）です。

問題C.ミツバチ

問題の著者-jakubr（Jakub Radoszewski）
入力ファイル名 ：stdin
出力ファイル名 ：stdout
制限時間 ：5秒
メモリ制限 ：512 MB

養蜂家バイタザールの趣味は、ミツバチによってもたらされた蜂蜜によって蜂の巣に形作られる人物の研究です。 このような各図は、側面1の六角形セルの接続セットを表し、内部には「穴」はありません。

より正式には、 「穴」のない図形を通常の六角形グリッドの単位六角形のサブセットと呼び、それに属する任意の2つの単位六角形がパスで接続され、そのすべての六角形もこのセットに属し、任意の2つの隣接する（このパスの意味で）六角形が共通の側面を持つ、このサブセットに属さない2つのユニット六角形は、このセットに属するセルの1つではなく、パス（2つの隣接する（このパスの意味）の六角形）によって接続されています 長老には共通の側面があります。

バイタザールは、可能な境界値とそのようなパターンのセル数の完全なリストを作成したいと考えています。 彼は、与えられた2つの数字nとpを使用して、境界がpであるn個のセルで構成される「穴」のない図形が存在するかどうかを調べるプログラムを作成するように依頼しました。

たとえば、次の図では、 n = 4、 p = 18です。



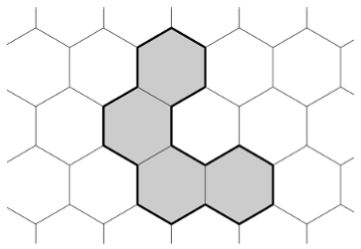入力ファイルの形式。 入力の最初の行には、テストケースの数T （1≤T≤1000）が含まれます。 次のT行はそれぞれテスト例を示し、2つの整数nとp （1≤n、p≤1000）-図の必要な面積と周囲長を含みます。

出力ファイル形式 。 各テストケースについて、入力ファイルに表示される順序で、個別の行に回答を出力します。 指定されたパラメーターを持つ図が存在しない場合は、「NO」を出力します。 それ以外の場合は、「L」と「R」で構成されるp文字の文字列を出力します。これは、図の周囲（時計回りまたは反時計回り）に沿ったパスを定義します。「L」は左折を示し、「R」は右を示します。

正解が複数ある場合は、それらのいずれかを印刷します。

標準	標準
3 4 18 3 18 3 12	RLRRRRLRLRLRRRRRRLRL いや LRRRLRRRLRRR

問題Cの解決策

課題は、六角形の格子に多角形を構築することです。
n個のユニットセルとp辺で構成されるか、これらのパラメーターを持つポリゴンが存在しないことを確認してください。

セルの数nを固定し、 p辺を持つポリゴンが存在するようにpの可能な値を調べます。 明らかに、 pは偶数でなければなりません。

また、 pが4 n + 2（行のn個のセルで構成され、辺に接するポリゴンの周囲。このポリゴンをチェーンと呼びます）より大きくすることはできません。

一方、最小境界のポリゴンは一種の大きな六角形であることは、一般的な考慮事項から明らかです。 正式には、その境界は次の式で与えられます 。

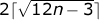
これらの制限は必要なだけでなく、十分であることがわかります。

構築アルゴリズムは次のとおりです。n個のセルで構成され、最大境界を持つチェーンから始めます。 さらに、多角形の周囲がpより大きい間、多角形の「尾」から1つのセルを削除し、このセルを「頭」に追加して、大きな六角形をレイヤーごとに構築します（図の矢印1を参照）。



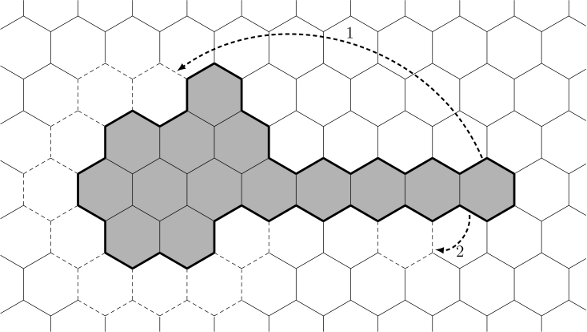
この移動により、境界線が2、4、または6減少します。そのため、最終的に境界線を2または4増加させる必要があります（たとえば、図の矢印2に従って「尾」からセルを移動します）。

一部の実装では、 nの小さい値の場合と、特定のnの境界が最小値に近い場合のケースを個別に分析する必要があります。

問題D.アニーとキューブ

問題と分析の著者はRoman Udovichenkoです。

入力ファイル名 ：stdin
出力ファイル名 ：stdout
制限時間 ：2秒
メモリ制限 ：512 MB

リトルアニーはキューブで遊ぶのが大好きです。 彼女は1からNまでの番号が付けられた行に配置されたN個のポジションがあり、キューブからタワーを構築するのが好きです。
タワーとは、いくつかの立方体が重なり合っていることです。 塔の高さは、その中の立方体の数です。 タワー番号は、このタワーが建設されている位置番号に対応しています。

最初は、すべてのポジションが空です。 毎分、次のことが起こります。

1. Anyutaは、 N -1から1までの数字の位置を順番に調べます。
2. 任意の位置iにキューブがあり、タワーの高さが位置i + 1のタワーの高さ以上である場合、Anyutaはi番目の位置から（ i + 1）番目にダイを1つシフトします。
3. Anyutaはすべてのポジションを確認した後、ポジション番号1のタワーにダイスを1つ追加します。

例 。 位置の数をN = 6とし、塔の高さを5 0 1 3 4 1 （1からNまでの左から右への番号付け）とします。 その後、次の数分で次のことが起こります。

1. Anyutaは位置5を見ます：その中の塔の高さは4で、次の位置の塔の高さは1です。Anyutaは位置5から位置6に1つのダイスを移動します。塔の高さは5 0 1 3 3 2になります。
2. Anyutaは位置4を見る：その中の塔の高さは3であり、次の位置の塔の高さは3である。Anyutaは位置4から位置5に1つのダイスを移す。塔の高さは5 0 1 2 4 2になる 。
3. 位置3から位置4までのAnyutaは、位置4のタワーの高さが位置3のタワーの高さよりも大きいため、キューブを転送しません。
4. 位置2から位置3まで、Anyutaはダイスを転送しません。位置2にはダイスがないためです。
5. 最後に、位置1から位置2まで、Anyutaは1つのダイスを転送します。 塔の高さは4 1 1 2 4 2に等しくなります。
6. これらのアクションの後、Anyutaは位置番号1にキューブを1つ追加し、タワーの高さは5 1 1 2 4 2に等しくなります。

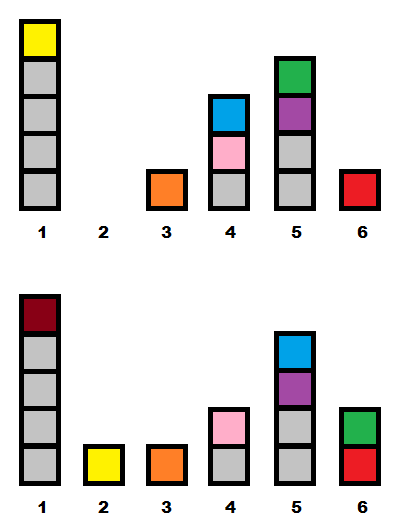上記の例でタワーの高さを1分で変更する

かつて、アニーはプレーにうんざりしていたので、一定の数分後に特定の位置にいくつのキューブがあるかを計算することにしました。 Anyutaはまだ小さく、キューブがたくさんあるので、彼女はあなたに助けを求めました。
より正式には、「 B _i分後にS _iからF _iまでの数字の塔の合計にいくつのキューブがあるか」などのQクエリに答える必要があります。 要求は独立しています。各要求では、最初はすべての位置が空であると見なされ、その後i> B _i分が経過します。

入力ファイルの形式 。 入力の最初の行には、2つの整数NとQ （2≤N≤10 18、1≤Q≤100 000）-タワーの位置の数と要求の数がそれぞれ含まれています。 次のQ行のそれぞれには、3つの整数S _i 、 F _i 、およびB _i （1≤S i≤F i≤N 、1≤B i≤10 ¹⁸ ）が含まれています-要求の開始位置と終了位置、および経過後の分数パンジーアクションの始まり。

出力ファイル形式 。 クエリごとに1行、Q行を印刷します。 各行に1つの数字を印刷します-リクエストへの回答。 入力に表示される順序で要求に応答します。

例

標準	標準
10 3 1 1 1 1 10 100 10 10 11	1 100 2
1,000,000,000,000 2 1 1234 412412314 100000000000 999999999999 1000000000010	1234 900000000006

問題Dの解決策

まず、キューブがどのように位置を移動するかを理解する必要があります。 たとえば、 N = 5の場合を考えます。

最初の5分間で、各位置に1つのキューブが表示され、タワーの高さが[1、1、1、1、1]になるまで、キューブは位置番号1から位置Nまで1つずつ「クリープ」します。
6分目に、立方体は4番目の位置から5番目に移動し、左側の立方体は1つの位置に右に移動し、位置番号1に新しい立方体[1、1、1、1、2]が表示されます。
7分目に、キューブはそれぞれ位置（3,2,1）から位置（4,3,2）にのみ移動し、高さは[1、1、1、2、2]になります。

8分で、キューブは位置1〜4から移動します：[1、1、1、2、3]。

シミュレーションを続けると、以下が得られます。

• 9分：[1、1、2、2、3]
• 10分：[1、1、2、3、3]
• 11分：[1、1、2、3、4]

さらに4分後、塔の高さは等しくなります[1、2、3、4、5]。 さらに5分後、高さは[2、3、4、5、6]になり、さらに5〜-[3、4、5、6、7]になります。

したがって、次のパターンに気付くことは難しくありません。

1. 最初のN分では、塔の高さは[1、...、1、0、...、0]です。
2. さらに、塔の高さの形式は[1、...、1、2、3、...、 x ]、または[1、...、1、2、3、...、 k -1、 kのいずれかです 。 k 、 k + 1、...、 x ];
3. 後 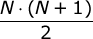塔の高さの始まりから数分後の形式は[1、2、3、...、 N -1、 N ]です。
4. その後、1つのサイコロがすべてのタワーに追加されます。

上記を考えると、各要求に答えるために、まず塔の高さの種類を計算し、次に数列に関連するいくつかの簡単な数式を適用する必要があります。

タスクE.数学マジック

タスクとレイバーの作者はオレグ・クリステンコです
入力ファイル名 ：stdin
出力ファイル名 ：stdout
制限時間 ：2秒
メモリ制限 ：512 MB

かつてヴァシャは数学オリンピアードの準備をしていましたが、眠りに落ちました。 Vasyaは、次のように言ってDavid Blaineを夢見ました。

「今、数学の魔法を示します。 ここを見てください：私はボード上に1より大きく2 ⁶³より小さいN個の正の整数を書いています。 これらの番号の一部は繰り返されます。少なくとも1つはシリーズの他の番号と同じです。 それらの下で、ボード上に、1より大きく2 ⁶³より小さい一連のK < N正の整数を書き込みます。これらの整数のいくつかも繰り返されます。 両方のセットの数値を乗算します... 2番目のセットの数値の積は、最初のセットの数値の積よりも正確に1大きくなります。

そして今、上段の数字の繰り返しをいくつか削除します。上段にある数字のセットは同じままですが、シリーズの少なくとも1つの要素を消去します。 一番下の行でも同じことを繰り返します...繰り返しますが、行の1つの数字が完全になくなったわけではなく、一部の数字が少なくなっています。 繰り返しますが、セットを乗算します...そして、2番目のセットの数値の積は、1番目のセットの数値の積よりも正確に1大きいことがわかります。 マジック！」

Vasyaは目を覚ましたが、 Nしか覚えていなかった。 彼が焦点を取り戻すのを助けてください。

入力ファイルの形式 。 入力ファイルの最初の行には、単一の整数N （2≤N≤100）が含まれています。これは、David Blaineによって最初に書き込まれたセット内の数字の数です。

出力ファイル形式 。 最初の行では、David Blaineが最初に書いたセットを印刷します。2番目の行-3番目と4番目の行の下に書かれた行-Davidによる削除後のこれらのセットのバリアント。 各セット内の数値は、降順で並べ替える必要があり、1より大きく、2 ^63-1を超えてはなりません。

条件と制限を満たすセットがない場合は、代わりに「Impossible」という単語を1つ出力します。 そのようなセットが複数ある場合は、それらのいずれかを印刷します。

標準	標準
2	不可能
3	2 2 2 3 3 2 3

解析問題E

N = 2の場合、解はありません（ K < Nなので、1つの数値が下部に書き込まれ、倍数を越えることは不可能です）。 N = 3の場合、解は8、9、2、3（{222}、{33}、{2}、{3}）であり、この解が一意であることを示すことができます。 N = 4の場合、解はありません。 証明は分析の最後に与えられます。

N≥5の解を構築します。

N > 4の場合、数値2（2 ^{N -3} -1）および2 ^{N -1} （2 ^{N -3} -1）をbおよびaとして使用します。
明らかに、それらは特定の2の数と2 ^{N -3} -1の積として表すことができ、 aはN因子の積として表され、 aはbで除算されます。 a +1とb +1の条件をチェックします。 a + 1 =（2 ^{N -2-2} ）+ 1 = 2 ^{N -2-1} 、およびb + 1 = 2 ^{N -2} （2 ^{N -2-2} ）+ 1 =（2 ^{N -2} ） ^2- 2 * 2 ^{N -2} + 1 =（2 ^{N -2-1} ） ² 、つまりa + 1 =（ b +1） ²となるため、
問題の条件を満たす2つと1つの数字のセットをそれぞれ取得します。

5≤N≤65の場合、この方法で生成された回答は自動的に適切です。

さらに、集合q ₁ 、...、 q _kがN = kおよびq _k = r ₁・r ₂の問題の解である場合、集合q ₁ 、...、 q _k-1 、 r ₁ 、 r ₂は、 N = k + 1の問題の解決策です（ bの展開の数値{ q _k }は、数値r ₁とr ₂の積として単純に表します）。 同様に、因子の1つを2つの小さい因子の積に分解すると、ペア （ a +1） 、 （ b +1）も正しいペアになります。

したがって、 2 ^{N -3-1}を2 ^63-1を超えない係数に分解し、 N + 1からN + D-1の数の同じ解から得ようとします。Dは2 ^Nの素数の数です。 ^-3-1 。 N > 65の場合でも、 2 2 ^{N -2-1}を2 ^63-1を超えない係数に分解する必要があります。

Nの剰余が0モジュロ6の場合、 N -2は2で除算され、 N -3は3で除算されるため、 2 ^{N -2-1}は（2 ^{（ N -2）/ 2-1} ）（2 ^{（ N -2）/ 2} + 1）および2 ^{N -3-1-} （2 ^{（ N -3）/ 3-1} ）（2 ^{（2 N -6）/ 3} + 2 ^{（ N -3）/ 3} + 1） 。 N≤95の場合、両方の係数が2 ^63-1を超えないことがわかります。 その場合、その後のすべての分解も問題の要件を満たします。

Nの剰余が5モジュロ6の場合、 N -2は3で割り切れ、 N -3は 2で割り切れます。同様の分解を使用します。

したがって、 N = 63（2 ⁶⁰ -1は多数の要因に分解される必要があり、 2 ⁶¹ -1は問題の要件を満たします）で開始し、96を超えないすべてのNを反復処理し、6で割ると0または5になります前の段落で説明した方法での2 ^{N -3-1}の最初の因数分解（その後、各要因<<ストップ>>に展開）、およびこの方法に従って、 2 ^N -2-1を2つの要因に因数分解します。 さらに、セットa + 1の因子Kの数は4に等しくなり（数の2乗は2つの数の積の2乗になります）、条件K < Nが満たされます。列挙の結果、次のようになります。

• N = 63の場合、 D = 13の係数を取得します。つまり、64≤N≤75の答えを生成します。
• N = 71の場合、 D = 7の因子を取得し、72から77までのNの回答を生成します。
• N = 77の場合、 D = 4の因子が得られ、78から81までのNに対する回答が生成されます。
• N = 78の場合、 D = 7の因子を取得し、79から84までのNの回答を生成します。
• N = 83の場合、 D = 11の因子を取得し、84から93までのNの回答を生成します。
• N = 90の場合、 D = 6の因子を取得し、 Nに対して91から95までの回答を生成します。
• N = 95では、 D = 9の因子が得られ、96〜100（最大104まで）のNの回答が生成されます。

したがって、アルゴリズムはすべてのN≤100の解を見つけます。

N = 4の解の不可能性の証明

N = 4なので、問題の条件により、 a + 1は3つ以下の要因に分解されます。 何かを消すには、少なくとも2つを繰り返す必要があります。 また、問題の条件により、 aはbで除算されます。つまり、 a = x b 、 x > 1です。

まず、 a + 1のすべてのセットオプション（およびb + 1の対応するセット）を分析します。

1. u ² 、 〜u ;
2. u ³ 、 〜u ;
3. uv ² 、 uv ;
4. u ³ 、 u ² 。

ケース3では、 a + 1 = uv ²です。 それからb + 1 = uv ; x b + 1 = uv ² 、減算uv （ v -1）= b （ x -1） 。 uvとbは互いに素であるため、 v -1はbで割り切れます。v > 1の場合、 v -1 = y b≥b nobr>、v≥b + 1です。 u > 1 なので 、 uv > v≥b +です。 論争。

この引数ではuvは使用されなかったため、ケースa + 1 = u ³およびb + 1 = u ^2が自動的に考慮されます。

ケース1（ u ² 、 〜u ）および2（ u ³ 、 〜u ） は残ります。 それらについては、aの4つの因子のセットとbの対応するセットのオプションを検討します。

I. a = x ² y z 、 b = x y z ;

II。 a = x ² y ² 、 b = x y ² ;

III。 a = x ³ y 、 b = x ² y ;

IV。 a = x ⁴ 、 b = x ³ ;

V. a = x ² y ² 、 b = x y ;

VI。 a = x ⁴ 、 b = x ² ;

VII。 a = x ³ y 、 b = x y ;

Viii。 a = x ⁴ 、 b = x 。

オプションIIからIVは、オプションIからそれぞれz = y 、 z = x 、およびz = y = xを代入することにより取得されます。 同様に、オプションVIはオプションVの特殊なケースです。

オプションIで 、 y zをtに置き換えます 。

1.x ² t + 1 = v ² 、 x t + 1 = v 、whence x ² t + 1 = x ² t ² + 2 x t +1。すべての項が正であり、 x ² t ² > x ² t （ t > 1であるため）、右側が左側より大きくなります。

2.x ² t + 1 = v ³ 、 x t + 1 = v 。 同様の括弧の置換と拡張により、 x ² t = x ^ 3 t ³ + 3 x ² t ² + 3 x tを取得します。すべての項は正で、 x ² t < x ³ t ³です。

オプションV

1.x ² y ² + 1 = v ² 。 整数x 、 y 、 v > 1の場合、すぐには発生しません。

2.x ² y ² + 1 = v ³ 、 x y + 1 = v 。 それらを置き換えて削減すると、合計（ x y ） ³ + 2（ x y ） ² + 3 x yは0になります。これはx 、 y > 1では不可能です。

オプションVII

1.x ³ y + 1 = v ² 、 x y + 1 = v、 x ³ y + 1 = x ² y ² + 2 x y + 1 、次にx y （ x ² - x y ）= 2として書き換える。 2がx yで除算され、 x > 1およびy > 1の場合は除算できないことがわかります。

2.x ³ y + 1 = v ³ 、 x y + 1 = v 。 代わりに、 x ³ y = x ³ y ³ + ... （ドットは明らかに正の数を示します）を取得します。これはy > 1では不可能です。

オプションVIII

x ⁴ + 1をx + 1で除算します。ただし、 x ⁴ + 1 =（ x + 1）（ x -1）（ x ² + 1）+ 2 、つまり2をx + 1で除算します。これは矛盾していますx > 1になるように。

すべてのケースを調べましたが、どこでも矛盾が生じました。つまり、 N = 4の場合、解決策はありません。

問題F.カバのシマウマとストライプ

タスクと論文の著者はrng58（副島真）
入力ファイル名 ：stdin
出力ファイル名 ：stdout
制限時間 ：2秒
メモリ制限 ：512 MB

ヒッポシマウマは10 ^18個のストリップを持ち、0〜10 18-1の連続した整数で番号が付けられています。時間0では、番号5⋅10 ^17のストライプのみが黒で、残りは白です。 時間 t （ t > 0）で、ストライプの色は次のルールを満たします。

• 時間t -1のx番目のストリップが黒の場合、時間tで黒になります。
• 時間t -1で、x番目のストリップからD以下の距離にあるすべてのストリップが白である場合（言い換えれば、10 ¹⁸未満の非負の整数すべてについて、不等式| x -y |≤Dを満たす場合、時間t -1 の y番目のストリップは白）、時間tで x番目のストリップも
  白。
• それ以外の場合、時間tでのx番目のストリップの色は任意に選択されます。

時間tでの10 ⁹ + 7を法とするシマウマの可能な異なる色の数を計算します。 少なくとも1つのストリップの色が異なる場合、2つのシマウマの着色ページは異なると見なされます。

入力ファイルの形式 。 入力の最初で唯一の行には、スペースで区切られた2つの整数tとD（1≤t≤10 9、1≤D≤50）が含まれています。

出力ファイル形式 。 単一の整数-時間tで可能な色の数を10 ⁹ + 7で割った余り

例

標準	標準
5 1	36
2 3	1849

タスクFの分析

対称性の考慮から、シマウマの色の数はその右半分の色の数の2乗であることは明らかです。 したがって、シマウマの右半分のみを検討します。 単純化するために、ストリップの番号を次のように変更します。500,000,000,000,000,000,000+xth xthとして番号を付けます。

: , t , . :

0, A .

:

• , .
• x — .
• d (0 < d ≤ D ) , ( x + d )- . d , .
• d A ( x + d )- .

.

, t A .

f ( a ₁ , a ₂ ,..., a _k ) — ,
A ={ a ₁ , a ₂ ,..., a _k }.

{ a ₁ , a ₂ ,..., a _k } , :

• 0-, a ₁ -, ( a ₁ + a ₂ )- — .
• i ( a ₁ +...+a _i +1)- ( a ₁ +...+a _{i -1} + D )- .

f ( a ₁ , a ₂ ,..., a _k ) = 2 ^{a ₁ -1 + a ₁ + a ₂ -D-1 + a ₂ + a ₃ - D -1 +...} .

, f ( a ₁ , a ₂ ,..., a _k ) ( k ≤ T ).

dp [ t ][ a ] ( t ≤ T, a ≤ D ) — f ( a ₁ , a ₂ ,..., a _t-1 , a).

:



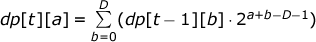
1 + dp [1][ D ] +… + dp [ T ][ D ], O(TD) .

, . v _t — ( dp [ t ][0],…, dp [ t ][ D ]) . , v _t+1 = v _t · A t ( A —
( D +1) × ( D +1)).

v ₀ ⋅ ( A + A ² +… + A ^T ) , .

— O( D ³ ⋅ log T ).



. ACM ICPC 2013 (Niyaz Nigmatullin) (mikhailOK), Facebook Hacker Cup, Google Code Jam . 2011, (Petr), - VK Cup 2012 (s-quark) .

, , , , , , . — Google, «» Facebook.