前の
記事で、検索を最適化するための発見的方法について書いた。 この記事では、別の、しかしすでに漸近的な最適化、つまり中間一致について説明します。
この方法の典型的な漸近縮約法は次のとおりです。

そして

。
エントリー
この方法は、タスクを半分に分割し、いくつかのデータを取得して、それらを互いに比較することです。
特定のタスクについて2つの条件が満たされている場合は、Meet-in-the-Middleが適用されます。
1)データの半分の処理時間は、最終回答を取得する時間よりも漸近的に短くなります。
2)半分の処理に関する情報を使用して、問題全体の答えを得るための漸近的に高速な方法があります。
理解するには、例を見てみることをお勧めします(予想される複雑さが増す順に与えられます):
例#1:列挙の最適化
N個の数字が与えられます。 合計が0になるように
k個の数字を選択する必要があります(同一の要素を複数回使用できます)。
単純なソリューション:
すべてを通過する

再帰中の量を再カウントする
k個の数字の選択肢。 漸近:
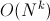
。
偶数
kの中間一致のソリューション:
1)見つけられる
kの数を
k / 2の2つの山に精神的に分割します。
2.1)すべてを書く

合計。
2.2)合計の配列をソートします。
2.3)各合計
sに対して、バイナリ検索
-sで見つけようとします。
2.4)見つけたら、ここに答えがあります。 そうでない場合、そのような組み合わせは存在しません。
3)利益:

。
このアルゴリズムを奇数
kに変更することは、あなたにとって難しいことではないと思います。
N = 30、
k = 12の場合、meet-in-the-middleは約1分間機能し、単純なアルゴリズムは17年間続きます。
例2:巨大な状態グラフで最短経路の検索を最適化する
マジシャンには36枚のトランプのデッキがあります。 最初は、順序は1、2、3 ...であり、特定の順列を
kステップ以下で取得したいと考えています。 各ステップで、マジシャンは
m枚の連続したカードをデッキの先頭に移動します。
課題は、彼が目的の順列を取得できるかどうかを調べることです。
状態グラフ
Sは、頂点がマップの現在の順列によって定義され、エッジが1つの順列で1つの順列から別の順列に移動する能力を持つグラフとして定義します。 このコラム36では注目に値します!

ただし、各頂点から36-
m +1のエッジがあり、これは比較的小さいです。
単純なソリューション:
状態グラフ
Sで幅優先検索を実行します
。 目的の状態に到達するか、
k +1の一番上のリモコンに到達したら、検索を完了します。 漸近:

。
ミートインザミドルを使用したソリューション:
1)開始頂点と終了頂点から最大深さ
k / 2で2つの幅検索を実行します。 2つのセットを作成します。幅優先検索がアクセスしたすべての状態。
2)これらのセットが交差する場合、方法があり、そうでない場合、方法はありません。
3)利益:
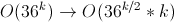
。
例3:「良い」サブセットの数を数える
オリンピアドニコフと脳を破壊したい人のためにグラフ
G (
N頂点)が与えられた。 列
Gの完全なサブグラフの数を数える必要があります(クリック)。
単純なソリューション:
すべてを通過する

サブグラフを作成し、それがクリークであることを確認します。 漸近:

。
このアルゴリズムは、次のように改善できます。

。 これを行うには、頂点のマスクを再帰的検索関数に保存する必要がありますが、これも追加できます。 このマスクをサポートすることで、「必要な」頂点のみを追加でき、最後に、クリックであるという事実をサブグラフで確認する必要がなくなります。 頂点を追加できます
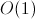
現在のマスクのビット単位の「and」と追加された頂点の隣接行列行を使用します。
ミートインザミドルのソリューション。
1.1)グラフ
Gを
N / 2頂点で2つのグラフ
G1と
G2に分割します。 見つける

それらのすべてのクリック。 漸近:

。
ここで、グラフ
G1のクリックごとに、グラフ
G2のクリック数を見つけて、それらの和がクリックになるようにする必要があります。 彼らの合計が最終的な答えです。
グラフ
G1の 1つのクリーク
Kについて、 G2にはいくつかの適切なクリーク
が存在する可能性があるため、前の2つの例と同じ方法を使用すると失敗します。 しかし、クリーク
Kの唯一のオブジェクトは、グラフ
G2の頂点のマスクであり、これも追加できます。 事前計算には多くの時間があり、これを使用する必要があります
。G2の各マスクについて、答えを計算する必要があります。
1.2)動的計画法を使用して、グラフ
G2の頂点の各マスクに対して、頂点が選択されたマスクのサブセットであるクリック数
を計算します。 状態の数:

。 遷移の数:

。 漸近:

。
Pythonでの再集計は次のとおりです。
for mask in range(1 << N): dp[mask] = 1 + sum([dp[mask & matrix[i]] for i in range(N) if ((mask & (1 << i)) > 0)])
2)グラフ
G1の各クリーク
K (空のものを含む)について、
K (空のものを含む)に追加できる計算されたクリック数をグローバル応答に追加します。 漸近:

。
3)利益:

。
おわりに
ミート・イン・ザ・ミドルの概念を明確に説明できたと思います。 ご質問がある場合は、コメントでお尋ねください、私は答えようとします。 ご清聴ありがとうございました。