こんにちは、Habr！
アルゴリズムをテストするとき、私はしばしばランダムなバイナリツリーを生成するタスクを持っています。 さらに、ウィッシュリストはランダムなツリーではなく、均一な分布から取得されます。 見かけの単純さにもかかわらず、このようなツリーを効果的に構築することは完全に重要です。
この記事のタイトルには「ブラケットシーケンス」という単語が含まれています。 これらの単語の背後には、ブラケットの助けを借りて、バイナリツリーを含む非常に多様なオブジェクトを記述することができるため、さらに何かが隠されています。 Habréでは、この事実について
別の投稿が行われました。
この記事では、線形時間を含むランダムブラケットシーケンスを生成するいくつかの方法を説明し、シーケンスをバイナリツリーに変換する例を示します。 面白い？
挑戦する
nを指定すると、長さ2 nのすべての正しいシーケンスの一様分布に従って、正しいブラケットシーケンスを生成します。在庫
長さ2
nの通常のブラケットシーケンスの数は、カタロニア語の
n番目の数に等しいことが知られています。
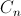
。 カタロニア語の数を計算するには、明示的な
そして再帰的
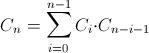
数式。
乱数ジェネレーターが必要です。
nが与えられると、0から同じ確率の乱数を生成します。
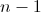
。 また、リストに対するランダム順列ジェネレーターが役立ちます。 Pythonでは、random.shuffleと呼ばれます。 線形時間で動作し、シーケンス1,2、...、
nの一様分布に従ってランダムな順列を生成すれば十分です。
Avosと言う3つの方法
動的プログラミングの力
すべての正しいブラケットシーケンスに番号を付けることができるという考えがあります。 また、たとえば、これを行う方法の詳細な説明があります。 そのため、このような計画を実装できます。
- カタロニア語のn番目の数を考慮します。
- 1〜の乱数を生成します 。
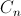- 動的計画法と組み合わせカウントを使用して、ブラケットシーケンスをその番号で復元します。
計画はほぼ優れています。 つまり
nが30未満の場合、計画は非常に良好です。しかし、nが1千のオーダーであることが判明した場合、長い計算が必要になります。 そのような計画に遅れずについていくために、私はたくさん汗をかかなければならないと思う
。 別の方法を探しましょう。
試してみてください
カタロニア語の数値の明示的な式をもう一度見てみましょう。
。
実際には、多くの正しいブラケットシーケンスがあることを意味します。
開いたり閉じたりする括弧の数が同じ場合、
バランスの取れたシーケンスを呼び出します。 たとえば、シーケンス
")(()" 、
"()()"はバランスが取れていますが、シーケンス
"()))"はバランスが取れていません。 明らかに、正しいシーケンスはバランスが取れています。 合計で、長さ
2nのすべてのバランスの取れたシーケンスが存在します
。 これらのシーケンスのいずれかがランダムに選択された場合、それは確率で正しいでしょう
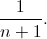
新しい計画。
- 一様分布に従って、ランダムバランスブラケットシーケンスを生成します。
- 正しいことを確認してください。
- シーケンスが正しい場合、推測します。 そうでない場合は、手順1に戻ります。
最初の段落から始めましょう。このようなランダムなブラケットシーケンスを生成する方法です。 任意のバランスの取れたシーケンスを取り、random.shuffleを介してミックスしましょう。
seq = ['(', ')'] * n random.shuffle(seq)
一枚の紙とペンを持って座っている場合、バランスの取れたブラケットシーケンス
xには正確に存在することが理解できます。
任意の初期平衡シーケンスを
xに変換する順列。 したがって、random.shuffleは、均等な確率でバランスの取れたシーケンスを生成します。 アルゴリズムを取得します。
def tryAndCheck(n): seq = [')', '('] * n while (not correct(seq)): random.shuffle(seq) return seq
時間を評価するために残っています。 正しいおよびrandom.shuffleルーチンは1行ごとに機能します。 メインループの反復はいくつになりますか？ 正しいブラケットシーケンスが確率で生成されることがわかっています
。 それから、ワシが確率で落ちるコインがあると言えます
。 マットを計算する必要がありますが、ワシが落ちるまで投げるのを待ちます。
オプションとして、マットをペイントすることもできます。
または、
よく知られている事実を活用してください。 いずれにせよ、マット。 アルゴリズム全体の待機時間は
。
試して修正する
わかりましたが、本当に大きなシーケンスが必要な場合はどうでしょうか？ 100万文字ごとのシーケンス。
線形アルゴリズムはもはやそれほど簡単ではありません。 1992年に、マイク・アトキンソンとジョージ・サックによって
別の記事が彼に捧げられました。 ここで、記事に書かれていることについての私のビジョンを提示します。
マジック関数
fが必要です。 入力では、関数はバランスのとれたブラケットシーケンスを取り、出力では同じ長さの正しいものを返す必要があります。 関数がシーケンスを均等に分散させること、つまり、すべての通常のシーケンス
y に対して 、
f（x）= yのような正確に
n + 1のバランスの取れたシーケンス
xがあることを確認することが重要です。 関数が線形時間で計算できる場合、ポイントはハット内にあります。
一様分布に従って、括弧で囲まれたバランスのとれたシーケンス
xを生成し、f（x）を返します。
関数内のすべてのトリック。 必要に応じて、停止して自分で考え出してみることができます。 機能しません、大丈夫です。 今、私はシリンダーから数学のシリンダーからウサギを取り出し、誰もが大丈夫です。
カウンターがあり、最初はゼロであるとします。 シーケンスを見ていきましょう。 各開き括弧に対して、ポイントを追加し、閉じ括弧ごとに減算します。
balance = 0 for c in seq: balance += 1 if c == '(' else -1
下のグラフは、シーケンスに沿って移動すると
balanceカウンターがどのように変化するかを示しています。
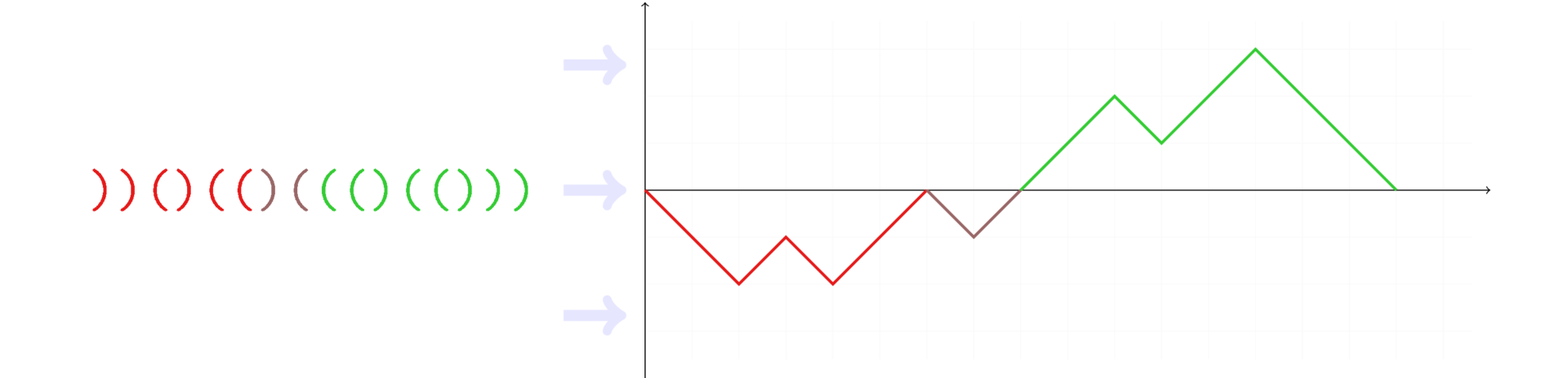
別々の色でペイントされたシーケンスは、分解不能と呼ばれます。 つまり 一般に、シーケンスのカウンターが開始点と終了点でのみゼロ値をとる場合、シーケンスは分解できません。 分解できないシーケンスは2つのカテゴリに分類されることに気付くかもしれません：完全にゼロレベルを超えるものと、それ以下のカテゴリです。 前者は正のシーケンスと呼ばれ、後者は負のシーケンスと呼ばれます。
負のサブシーケンスの合計の長さを計算し、半分に分割します。 得られた値はシーケンス欠陥と呼ばれます。 正しいシーケンスの欠陥はゼロです。 長さ2
nの正しいシーケンスのすべてのブラケットを逆のブラケットに置き換えると、欠陥は
nになります。
注意、ウサギ！ チャンフェラーの定理。 欠陥
kを持つ長さ2
nのブラケットシーケンスの数は、カタロニア語の
n番目の数に等しい
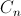
そして
kに依存しません。
定理は、長さ2
nのすべてのバランスの取れたシーケンスを同じサイズの
n + 1クラスに分割し、クラスの中にすべての正しいブラケットシーケンスを含む別のクラスがあるという点で興味深いです。 したがって、欠陥
kを持つすべてのシーケンス
xを正しいシーケンス
yでエンコードする関数を考え出すことができます。この場合、シーケンス
yと欠陥
kから一意に
xを再構築できます。
このような関数を思いついたら、すべての正しいシーケンス
に対して 、0から
nまでの欠陥とバランスが取れた正確に
n + 1が存在することになります。 簡単そうです。
試み1。
すべての負のサブシーケンスを取り、反転します。 ブラケットを反対側に交換します。
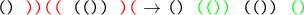
そのような機能に加えて、すべての分解不能なシーケンスの位置を保持します。 マイナス-どのサブシーケンスが負で、どのサブシーケンスが正であったかに関するすべての情報を失います。 欠陥が3であることを知っていても、この例から初期シーケンスを復元することはできません。
試行2。
すべての負のサブシーケンスを反転して、最後に配置しましょう。
これで、欠陥がわかったので、負のサブシーケンスを回復できます。 しかし、我々は彼らがいた位置を失いました。
試み3。
任意の分解不可能な負のシーケンスを取り、その極端な括弧を切り取り、結果を逆にします。
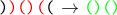
このような操作は、unningな反転と呼ばれ、
gで示されます。 シーケンスは分解不能で負なので、結果は常に正しいブラケットシーケンスになります。 関数
gの秘Theは、一方では可逆的であり、他方では、負のサブシーケンスの位置をエンコードするために使用できる2つの追加のブラケットがあることです。
試行2を完了したのは、負のシーケンスを逆の順序で取り出し、
g関数を介して巧妙に反転させるだけです。
例からわかるように、負のサブシーケンスの位置は、フリーブラケットで示されます。 私はそれらを青でハイライトし、正方形にしました。 文字
eは空のシーケンスを意味します。
どのブラケットが緑色で、どの青色が不良であるかを調べます。つまり、初期シーケンス自体を復元できます。 これが必要なものです！
アトキンソンとサックは、関数fの再帰式を提案しました。
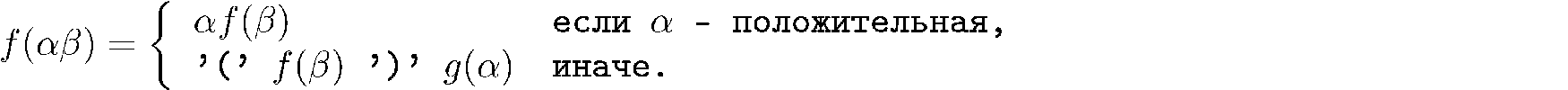
ここに
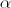
分解不能なサブシーケンス
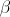
-残り。
以下に、拡張再帰を使用したPythonのアルゴリズムの実装を添付します。 アルゴリズムが線形時間で実行されることは簡単に理解できます。
def tryAndFix(n): seq = ['(', ')'] * n random.shuffle(seq) stack = [] result = [] balance = 0 prev = 0 for pos in range( len(seq) ): balance += 1 if seq[pos] == '(' else -1 if balance == 0: if seq[prev] == '(': result.extend( seq[ prev : pos + 1 ] ) else: result.append('(') stack.append( [ ')' if v == '(' else '(' for v in seq[ prev + 1 : pos ] ] ) prev = pos + 1 for lst in reversed(stack): result.append(')') result.extend(lst) return result
ツリー生成
この場所まで読んでいただければ、とても嬉しいです。 あとは、シーケンスをツリーに変換するだけです。
長さ2
nのブラケットシーケンスは、
n + 1頂点を持つ任意のアリティの木を完全にエンコードします。 実際、詳細な検索を実行します。 上部の入り口で、開始ブラケット、出口で閉じブラケットを書きます。
同時に、
n + 1からの任意のアリティの木は、
n頂点からの二分木と1対1で対応させることができます。 必要なのは、最初に任意のアリティの木を「左の子-右の隣人」の形式で書き留めてから、右の隣人を右の子に名前変更することです。
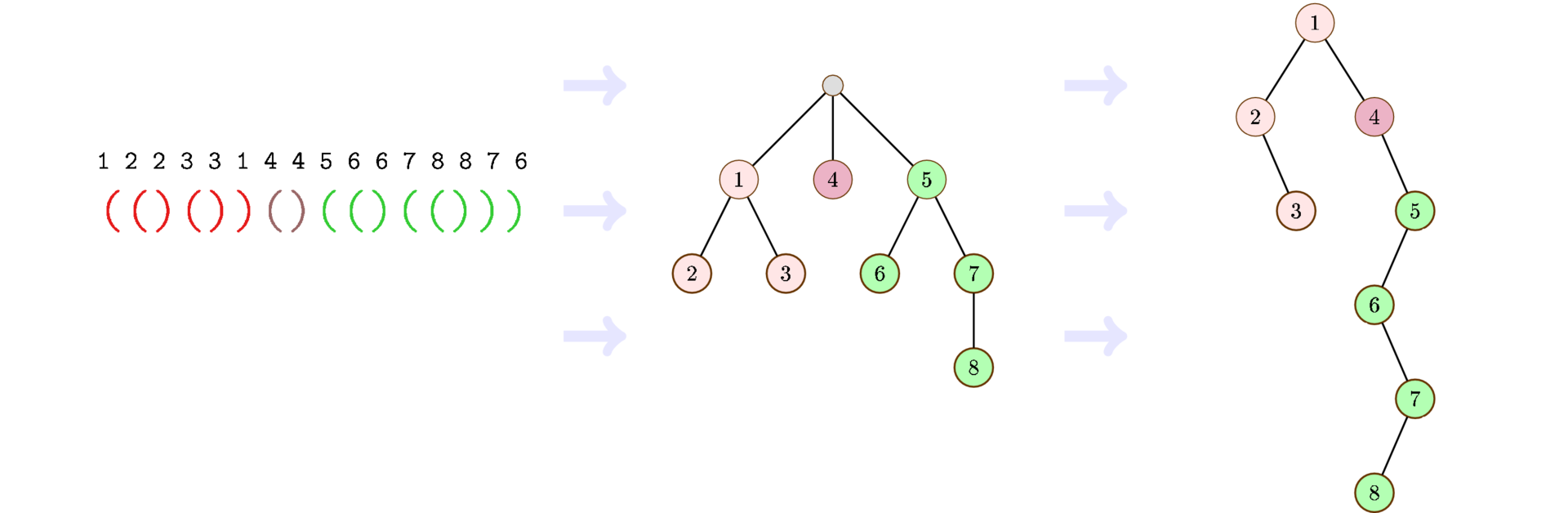
一緒にいてくれてありがとう！
参照資料