SOAの一部としてトランスポート問題を解決する遺伝的アルゴリズム
著名なHabrasocietyへのご挨拶!
この記事では、遺伝的アルゴリズムを使用して輸送の問題をどのように解決したかについてお話したいと思います。
タスクステートメント
ウィキペディアでは、次のように問題を定式化しています。つまり、静的データと線形アプローチを使用して、均質車両(所定量)の均質な可用性ポイントから均質な消費ポイントまでの均質な製品の最適な輸送計画の問題です。
たとえば、市内での水のボトルの配送、各顧客のニーズ、車両の収容能力、およびポイント間の距離を把握する必要があります。
さらに、さまざまな制限を追加できます。たとえば、一時的な配達時間帯、特定のマシンの特定のポイントへの訪問の除外などです。 これらの制限やその他の制限を当面の計画に追加しますが、現時点では、サービスは前の段落で定式化された問題を解決します。
遺伝的アルゴリズム
説明
このソリューションは、並列遺伝的アルゴリズムに基づいています。 各ソリューションは染色体で表され、別の染色体と交差させたり変異させたりすることができます。 その結果、結果の子が一般集団に追加されます。 母集団のサイズは制限されており、最も適合性の低い染色体は削除されます。
複数の分離された染色体集団が同時に発生するため、並列アルゴリズムが呼び出されます。 特定の時点で、ランダムに選択された染色体が集団間を移動します。
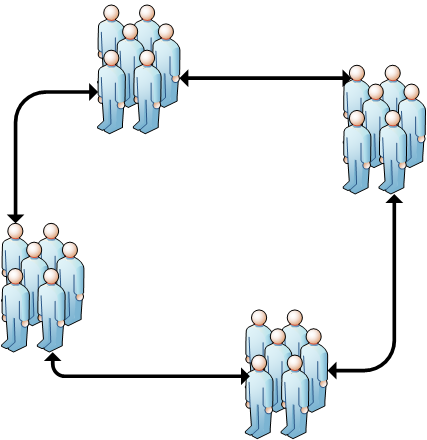
染色体表現
各染色体は問題の解決策であり、配列の配列として表されます。ここで、ネストされた配列はそれぞれ1つのルート(車で1歩)を表します。 配列の各要素は、商品を配達する必要がある顧客です。

すべてのルートは明らかに倉庫から始まり、暗黙的に終了します。
クロス
ランダム(ランダムクロスオーバー)と同種(均一クロスオーバー)の2種類のクロスがあります
ランダムな交差-親1からの任意のルートの任意の部分は、親2の最適な挿入場所に配置されます。最適な挿入場所は、最短の長さを与える場所です。
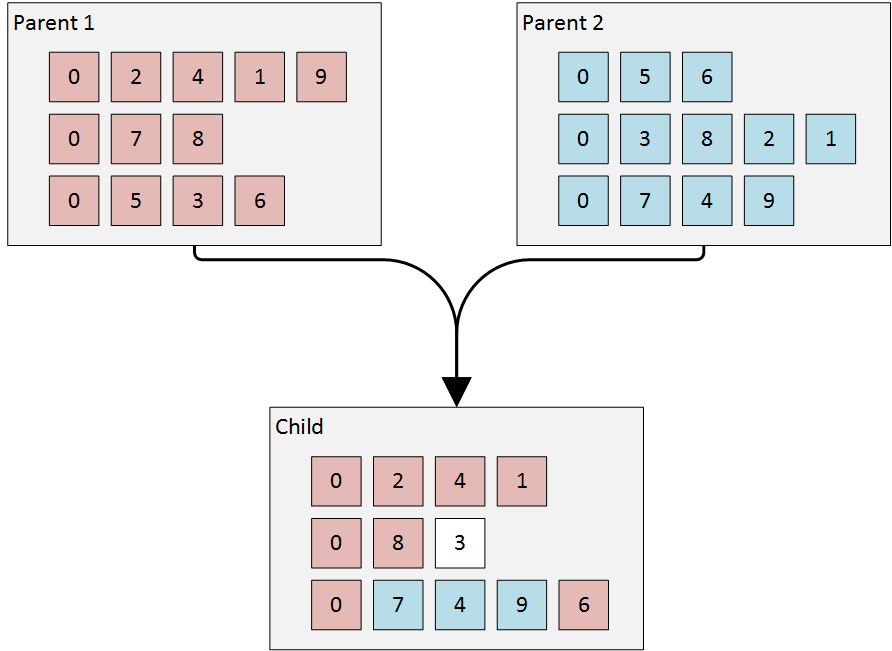
同種交配は、親のすべてのルートの密度インデックスを計算し、代わりに親1と2から最低のインデックスを持つルートを追加します。残りのポイントは、最適な挿入の場所に分配されます。
突然変異
アルゴリズムは2種類の突然変異を使用します-ランダムで、ルート突然変異の最も遠い部分を対象としています。
ランダムな突然変異は、ルートのランダムな部分の一部を切り取り、最小の合計距離を与える場所に挿入します。 2番目のタイプの突然変異は、ランダムルートで最も遠いクライアントを検出し、最適な挿入の場所に移動します。
ローカル最適化
交差操作と突然変異操作の後、アルゴリズムは各ルートのポイントを移動して、ルートの長さが最小になるようにします。
フィットネス機能
各染色体の適合度(品質)は、次の式で考慮されます。
フィットネス=合計距離+過負荷のペナルティ*過負荷+過負荷のペナルティ*過負荷
ルートの一意性の維持
より高速な解決のために、一意の染色体のみが各グループに含まれています。
計算終了
アルゴリズムは計算を完了して、最大数の時代を達成するか、特定の時代の改善がない場合
アルゴリズムの結果
以下は、タスクの標準セットのサブセットに対するアルゴリズムの結果です。 問題の名前の最初の桁はポイントの数であり、2番目は車の数です。 B-n31-k5-5台の車で31ポイント。
8核AMDの作業結果(8350):
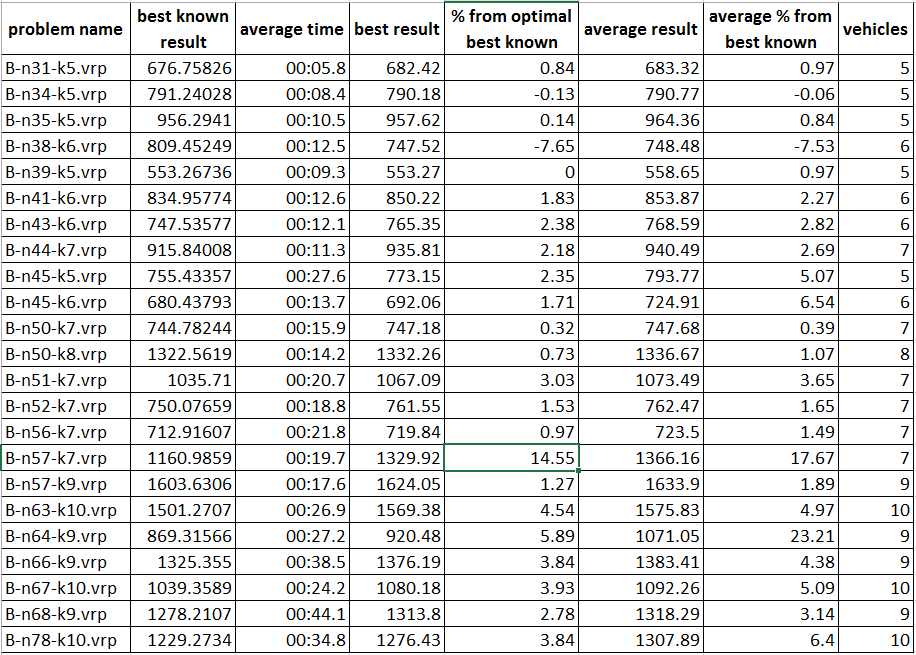
すべてのテストデータの作業結果は、プロジェクトページにあります。
ソリューションのアーキテクチャ
ソリューションはC#で記述されており、いくつかのサービス、データベース、およびキューで構成されています。
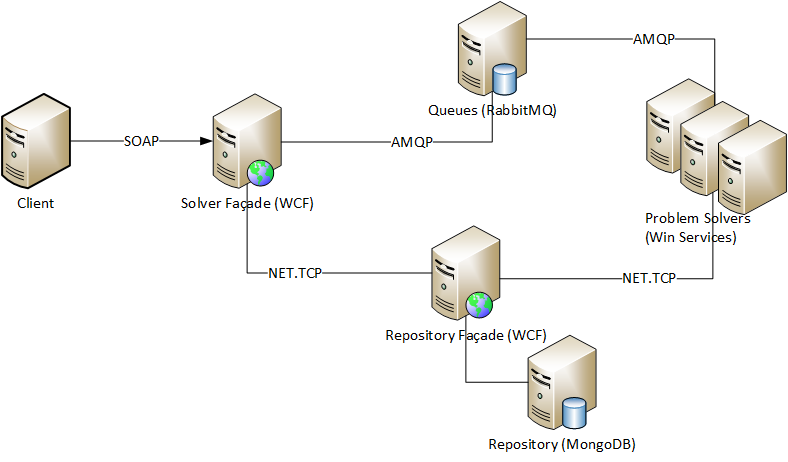
技術スタック:
1. .NET 4.5 / C#/ WCF / WinService
2.キュー:RabbitMQ
3. DB:MongoDB
4. DIコンテナ:Autofac
5.単体テスト:MS Test / Rhino Mocks / Fluent assertions
共有するために必要だと思う.NET固有の経験:
1.頻繁にアクセスされるコードのセクションでは、プロパティを使用せず、単にパブリック変数を使用します
2.配列は、挿入および削除操作を実装している場合でも、リストおよび辞書(辞書)よりも高速であることがよくあります。
次のステップ
現在のソリューションは無料で利用できます。
開発中の新機能のリスト:
1.ポイントの座標による距離の取得
2.制限の追加-時間枠、車、配達ポイントについて
参照資料
Googleには、遺伝的(だけでなく)アルゴリズムを使用して問題を解決することに関する多くの出版物が含まれています。 それらのいくつかの名前はここにあります:
1.
遺伝的アルゴリズムを使用した車両ルーティング問題の解決2.
時間枠を使用した配車ルート問題のハイブリッドアルゴリズム3.
時間枠付き車両ルーティング問題のためのルート指向ハイブリッド遺伝的アプローチ