ガントチャートを見るたびに[
1 ]
、私は同じ質問に苦しんでいます。 どうやって? リソースAがタスクBを5日間で完了することを確認する方法を次に示します。 いいえ、履歴データがあることを理解しています。統計という言葉を恐れていません。 しかし、このすべてに基づいて自信を持って予測を行うにはどうすればよいでしょうか? わかりません。
あなたにとって「イベントの相互依存」と「統計的逸脱」という用語が個別にだけでなく集合的にも何かを言っているなら、その記事はあなたの興味を引くことはないでしょう。 しかし、これらの用語が同じコンテキストで使用されている場合、ガントチャートの問題が何であるかがわからない場合は、簡単な例でこれを説明する猫に招待します。
たとえば、Webプロジェクトを開発する小さな会社を取り上げます。 会社は長い間運営されているので、十分に長い期間、完了したプロジェクトの統計さえ持っていると想定しています。 会社では、効率を高めるために、分業があります。 したがって、注文を完了するプロセスは、顧客との契約の締結、設計の開発、プロジェクトの実装、実装の4つの段階で構成されます。
実証するために、次の仮定が行われます。
- 各ステージには3〜7日かかります。 たとえば、マーケティング部門は当社のサービスを顧客に販売し、顧客と契約を結びます。 このプロセスには、3営業日(標準タスクのクライアントが標準契約に署名)から7営業日(顧客の代理人が出張に行き、契約に基づく追加の承認が表示されたため、高度な機能について話し合う必要があります) 設計者は、3日間(顧客は選り好みがなく、標準テンプレートに同意し、ロゴを作成し、いくつかの機能を作成する必要があります)から最大7営業日(設計者が病気になり、顧客がレイアウトに署名しません)から注文します。
- 毎日プロジェクトが完了する確率は、連続均一分布の法則に従って分布します[ 2 ] :
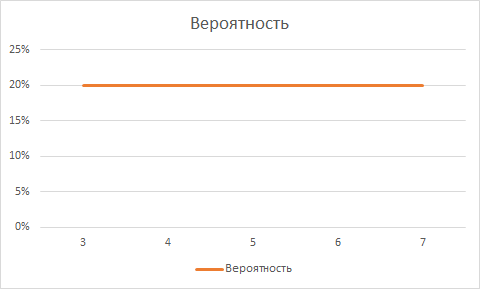
ほとんどの場合、これは確かにそうではなく、むしろ正規分布のようなものが観察されます[ 3 ] 。
- パラグラフ1および2の初期データを使用すると、数学的期待値[ 4 ] 契約期間は3 * 0.2 + 4 * 0.2 + 5 * 0.2 + 6 * 0.2 + 7 * 0.2 = 5営業日です。 つまり 平均して、各ステージは5日で完了します。
これらすべての仮定により、バランスの取れたシステムについて議論することができます。 または、言い換えれば、各ステージが少なくとも平均して同じ日数を要するシステム。 すべてがあなたのためにそのように正確に配置されている場合は、コメントでそれについて書いてください、私は白いen望であなたをvyましく思います 「狭いリンク」のない組織はまだ見ていませんが、あなたはすでにこれに取り組んでいます。
すべて、紹介の終わりに、このトピックに目を向けます。
最初のガントチャートを作成しましょう。 この図では、平均ステージ完了時間が5営業日であることがわかっているため、5つのプロジェクトを実装するのにかかる時間を取得します。

この図は、平均5日間で、いくつかの段階の遅れが他の段階の遅れによって相殺されるという古典的な仮定を表しています。 しかし、1つの小さなニュアンスがあります。 どっち? 例を示しましょう。 最初の段階から始めましょう。

ご覧のとおり、最初の段階は想定に適合しています。 つまり 一部のステージの減速は、他のステージの加速によって補償されます。 しかし、前述の「イベントの相互依存」がある場合、第2段階では状況はそれほどバラ色ではありません。

30営業日の代わりに、5番目のプロジェクトの第2ステージが33営業日に終了したことに気づきましたか? そして、「マネージャー」という悪夢があります。13、14、18、19、20営業日、従業員は何の関係もありません。 さて、最後の写真:

今、読者は「はい、彼はそのような例をセットアップしただけです!」という考えを持っているはずです。 残念ながら、私はしませんでした。 このような温室条件でも、5営業日のすべての段階で数学的予想を用いて1000回モデリングした後、日によってプロジェクトが完了する確率は次のようになります。

はい、最も可能性の高い値は44〜45日ですが、グラフを作成してみましょう。特定の日までにプロジェクトを完了する確率は次のとおりです。
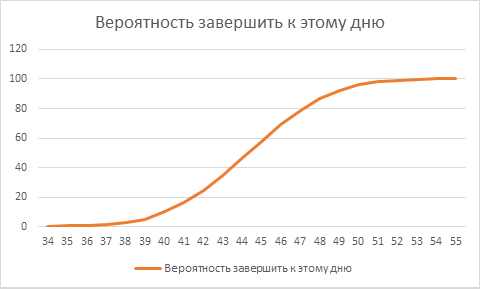
40日目までに、プロジェクトを完了する確率は約10%です。 44〜45日までに、すべてのプロジェクトを完了する確率はわずか50%です。 つまり、5回に1回しか顧客を欺かないことに同意する場合、80%を取得する必要があり、これはすでに48日です。 40日間という当初の計画から20%の偏差があります。 そして、これはすべてのプロジェクトが同じであるという前提で、バランスの取れたシステムにあります。
通常の法則に従って完了の確率が分配されると、状況はわずかに改善されます。 たとえば、数学的な期待値5と分散[
5 ]
0.5に等しい。 この場合、3から7のいずれかの日にステージを完了する確率は、次のように分配されます。
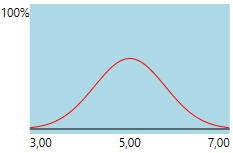
この分布では、特定の日までに完了する確率は次のようになります。
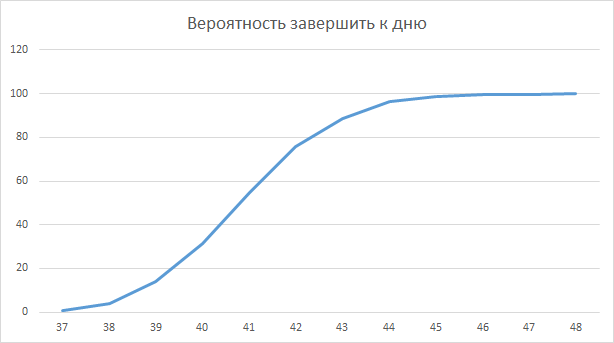
状況は改善されました。 計画された40日間で、30%の確率ですでに間に合います。 そして、43営業日までに、確率は80%になります。 残念ながら、実際のプロジェクトでは、そのような分散は非常に高い再現性でのみ発生します。 たとえば、組立ライン上。 ソフトウェア開発では、分散がより大きくなります。 ほとんどのプロジェクトはユニークであり、それらの人件費の範囲は非常に大きくなる可能性があります。
そして最後に、次の記事に注目を集めるための小さなスケッチ。 第1、第3、第4段階で期待値が4、第2段階で7シフトした場合、「理想的な」ガントチャートはどうなると思いますか。 3つのステージは平均で1日速くなり、1つのステージは2つ長くなりますか?
ガントチャートと1日で完了する確率
印象的? つまり、理論的にはプロジェクトの開発を1日短縮し、5つのプロジェクトの開発を6日遅らせました。 ただし、一方で、特定の日までに5つのプロジェクトを完了する確率図を見ると、次のようになります。
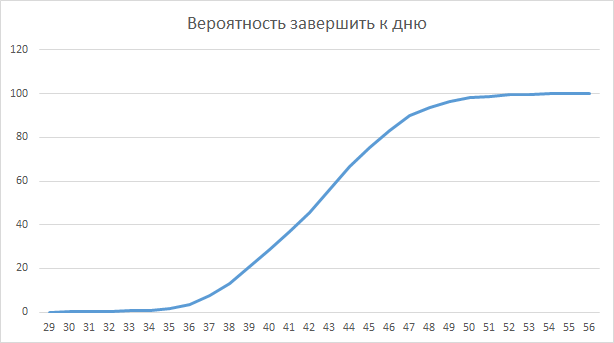
80%の確率で、ガントチャートから取得した46日目までに完了します。 注目されましたか? よし、次の記事でお会いしましょう。
追伸この記事を読んでアドバイスをいただき、Andrei Potapovと
CrazyViperに感謝します。 あなたとHabrのすべての読者に幸せなプログラマーの日を!
1.http :
//ru.wikipedia.org/wiki/Gantt Diagram [
to text ]
2.
http://ru.wikipedia.org/wiki/連続的な均一分布 [
本文へ ]
3.
http://ru.wikipedia.org/wiki/正規分布 [
テキストへ ]
4.
http://ru.wikipedia.org/wiki/数学的期待 [
テキストへ ]
5.
http://ru.wikipedia.org/wiki/ランダム変数の分散 [
テキストへ ]