🎛️ ⛹️ 👩🏻‍🏫 分布による別の並べ替え 👨🏼‍🏫 😼 🏷️

効率的なソートアルゴリズムになると、博学なhabruiserは、すぐに消えない「クイックソート」、最新の「ティムソート」、伝説の「マージソート」、さらにトリッキーな「内省的ソート」を思い出します。

上記の方法の有効性を疑問視することなく、特定の入力条件の下で、他のアルゴリズムを簡単に高速化するソートを提供します。

これはFlashSortで 、データが均等に分散された非常に大きな配列を適切に処理します。

1998年の方法は、ドイツの科学者Karl-Dietrich Neubertによって導入されました。彼の科学的研究は、アルゴリズムの理論ではなく、固体物理学、生物物理学システム、素粒子物理学に専念しています。実験結果を分析して、ノイバートは統計データの大きな配列はソートするのに非常に論理的であり、確率理論に頼るという結論に達しました。

エッセンス

操作の原理は、特定の例を使用して簡単に説明できます。

値の範囲が1〜100であるn要素の大きな配列があるとします。値が50の要素に出会った場合、その正当な場所は配列の中央にあると合理的に仮定します。状況は他の要素と同様です： 5は、おそらく、構造の始まりに近いはずです。95ほぼ終わりまでそれを押すことが適切です。このような不注意な操作の結果、 ほとんどソートされた配列がすぐに得られます。

急いで要素をスクランブルしましたが、障害のあるものをすばやく並べ替える方法を適用することが残っています（ 挿入によるソートが非常に適しています）。

マタン

主なタスクは、その値に応じて、配列のすべての要素をいくつかのクラスに分散する必要があるという事実に要約されます。最小の数値は最初のクラスにあり、最大の数値は最後のクラスにあり、残りの数値は中間グループにあります。

クラスの数にmを使用し、配列内の最小A _minおよび最大A _max要素もわかっている場合、要素A _iのクラス番号は次の式で計算されます。

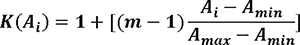
確率論の観点から、クラスKは、分布モデルにおける要素A _iの位置を示す変位値にすぎません。

式の角括弧は整数部分を意味します。したがって、クラスの番号は1からmに変更されます。追加の配列Q [ 1..m ]では 、対応するクラスに属するメイン配列の要素数が位置Q [ K ]に入力されます。

次に、追加の配列を使用して、メイン配列の要素を再配布し、それらをほぼその場所に挿入します。アルゴリズムのニュアンス-以下に示すJavaプログラムのコード。

可視化

所要時間は2分以上です。ソートが「ちらつき」と呼ばれる理由が明らかになります。

YouTubeバージョン

時間効率

すでに述べたように、アルゴリズムは、データが均等に分散されている大規模な配列で非常に効率的です。この場合、平均時間の複雑度がO（n）の FlashSortは、 QuickSortと他の効率的な並べ替え方法の両方を大幅に上回っています。

他の状況では、物事はそれほど素晴らしいものではありません。データのサイズが不均等に分散している短い配列、長い配列では、「ちらつきの並べ替え」は許容できるものの、はるかに控えめな結果を示します。

また、メインアルゴリズムを不完全に配列された配列に適用しても意味がありません。 挿入によるソートに直接進む方が簡単です。 FlashSortのほとんどソートされた配列は縮退したケースであり、特に失敗した状況では、最悪の時間が観測され、 O（n ² ）の複雑さがあります。

メモリ効率

このメソッドは、新しい配列（要素の数がクラスの数）のリソースを必要としますが、メモリをあまり必要としません。質問は非常に関連性が高い：何をとるべきかクラスが多いほど、分布は良くなりますが、追加メモリの形で価格が高くなります。ほとんどの場合、許容価格/品質比は次の式で与えられます

m≈0.42 n 、

Neubertにより経験的に導出されました。

メイン配列の要素の可能な値の範囲が十分に小さい場合、 mとして最小要素と最大要素の間の整数の距離をとることが可能です（さらには望ましい）。このような場合、条件"1 value = 1 class"を条件として、時間によるソートの速度は、ほとんどメモリを追加せずに最良の結果O（n）に達します。

実装

JavaのFlashSort。

import java.util.Arrays; public class FlashSortAlgorithm extends SortAlgorithm { void sort(int[] a) throws Exception { FlashSort(a); // FlashSort InsertionSort(a); //   } //FlashSort,    //   private void FlashSort(int [] a) throws Exception { int n = a.length; //  int m = n * 0.42; //  int [] l = new int[m]; //  int i = 0, j = 0, k = 0; //   int anmin = a[0]; //  int nmax = 0; //   //     for (i = 1; i < n; i++) { if (a[i] < anmin) anmin = a[i]; if (a[i] > a[nmax]) nmax = i; } // = ?   //   . // ,  ! if (anmin == a[nmax]) return; //   double c1 = ((double) m - 1) / (a[nmax] - anmin); //   //    - //     for (i = 0; i < n; i++) { k = (int) (c1 * (a[i] - anmin)); l[k]++; } //     //(  2-)   . //      //        //     for (k = 1; k < m; k++){ l[k] += l[k - 1]; } //        //         //       int hold = a[nmax]; a[nmax] = a[0]; a[0] = hold; //  // ,  //     int nmove = 0; // ,      //      ""  int flash; //   //  ,    //  j = 0; //    //      1..m-1 k = m - 1; while (nmove < n - 1) { while (j > (l[k] - 1)) { j++; k = (int) (c1 * (a[j] - anmin)); } flash = a[j]; while (!(j == l[k])) { k = (int) (c1 * (flash - anmin)); hold = a[l[k] - 1]; a[l[k] - 1] = flash; flash = hold; l[k]--; nmove++; } } } //    //     FlashSort private void InsertionSort(int [] a) throws Exception { int i, j, hold; for (i=a.length-3; i>=0; i--) { if (a[i+1] < a[i]) { hold = a[i]; j=i; while (a[j+1] < hold) { a[j] = a[j+1]; j++; } a[j] = hold; } } } }

コードはここから取られています、私のコメント。
さまざまなPL（Ada、C、Basic、Fort、Fortran、Java、Pascal）の実装のコレクションは、教授のWebサイトで見つけることができます。

アルゴリズムの特徴

役職	FlashSort（フリッカーソート、点滅ソート、点滅ソート）
著者	カール・ディートリッヒ・ノイベール
発行年	1998
クラス	分布ソート
持続可能性	不安定
比較	比較なし
時間の複雑さ	最悪の	O（n ² ）
	平均的	O（n + m）
	最高	O（n）
記憶困難	合計	O（n + m）
記憶困難	追加データ	O（m）

参照資料

英語版ウィキペディアのFlashSort
Karl-Dietrich Neubert、個人ウェブサイト。
Dr.のFlashSort ドブの日記
Javaの視覚化

分布による別の並べ替え

エッセンス

マタン

可視化

時間効率

メモリ効率

実装

アルゴリズムの特徴

参照資料

More articles: