今日は、11年前に発明されたばかりですが、3千年の歴史を持つ計数装置が「プロトタイプ」として機能する素晴らしいアルゴリズムに注目します。

著者

2002年、ニュージーランドのオークランド大学の3人の数学者、ジョシュアJ.アルラナンダム、 クリスチャンS.カリュード 、マイケルJ.ダイニーンによって選別が行われました。 科学者の活動分野は、離散数学、数論、量子コンピューティング、情報理論、組み合わせアルゴリズムです。

私は、3人のうちどれが元のアイデアを所有しているかは知りません。 おそらく、計算数学の歴史を教えているカルード。 誰もが知っているように、ヨーロッパのアカウントの祖先はそろばんであり、 そろばんはバビロンからエジプトに、そこからギリシャに、そこからローマに、ヨーロッパ全体に移住しました。 アンティークの「計算機」の外観と動作原理は、この「単純な」ソートの動作を連想させるため、「そろばんソート」とも呼ばれます。

アルゴリズム

自然数のセットをソートするとします。 互いの下に、ボールの対応する数の水平列の形で各番号をレイアウトします。 それでは、これらすべてのボールのグループを水平ではなく垂直に見てみましょう。 ボールを完全に押し下げます。 再び、水平に切り替えて、各列のビーズを数えます。 注文された番号の初期セットを取得しました。

実装

30以上のプログラミング言語でのビーズの並べ替えについては、 こちらをご覧ください 。 視覚的にはアルゴリズムはどこにも単純ではありませんが、ソフトウェア実装の観点からすると、これは非常に重要なソートです。

縮退ケース

これは逆順の配列です。 ボールの最大可能数は、最高点から崩壊する必要があります。

限られた適用性

この方法は主に自然数に適用できます 。

整数をソートできますが、これはより複雑です-負の数は正の数とは別に処理する必要があります。

整数に減らされる前に、ソートと小数を妨げるものは何もありません（たとえば、すべてを10 ^kで乗算し、ソートしてから10 ^kで除算します）。

もちろん、各行が正の整数として表される場合、行もこの方法でソートできます。 しかし、なぜですか？

時間の複雑さ

アルゴリズムを考慮するコンテキストに応じて、ソートにはすでに4つあります。

O（1）

抽象的なケース、真空中の球状ビーズの並べ替え 。 すべての移動するボールが同時に移動し、所定の位置に落ちると想像した場合。 これは、このソートでは実現不可能な複雑さです-アルゴリズムの理論でも実際でもありません。

O（√n）

ビーズが油性の良い編み針をすべる物理モデルの推定値。 自由落下時間は、最大高さの平方根に比例します。これは、 nの倍数です。

O（n）

まだその場所に到達していないボールは、1回の反復で一緒に1つの位置を移動します。 このソート方法を実装する物理デバイス、アナログまたはデジタルのハードウェア実装の場合、この複雑さについて話すのが適切です。

O（S）

Sは配列の要素の合計です。 各ボールは個別に動き、ボールのグループを同時に転がさないでください。 プログラミング言語で実装するための適切な複雑性評価。

記憶困難

希望するものを残します。 ビードソートは、贅沢な記録保持者です。追加のメモリのコストは、アレイ自体と平均O（n ² ）を保存するコストよりも何倍も高くなります。

物理学

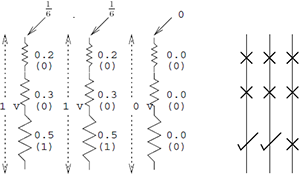
ボールの有無は、一連の電気抵抗器を通過するアナログ電圧として解釈できます。 ボールがそれに沿って移動するロッドは、 電気抵抗器に似ており、電圧は上から下に向かって増加します。

電気用語の舌で縛られた使用のために蹴らないでください、私は物理学の学校でプラス 4とマイナスのトリプルを持っていました。

このpdfドキュメントの詳細については、静電気の専門家を派遣します 。

実際に

ビーズソートは一種のカウントソートです。 各垂直トラックのボールの数は、垂直のシリアル番号以上の配列内の要素の数です。

アルゴリズムの特徴

役職	ビーズソート（ビーズソート）; そろばんソート
著者	ジョシュアJ.アルラナンダム、クリスチャンS.カルード、マイケルJ.ディニン
発行年	2002
クラス	分布ソート
持続可能性	持続可能な
比較	比較なし
時間の複雑さ	O（1）	O（√n）	O（n）	O（S）
記憶困難	O（n 2 ）

参照資料

オークランド大学のWebサイトでのビーズの選別
アルゴリズムに関する著者のドキュメント、pdf
さまざまなPLでの実装
英語版ウィキペディアのビーズの並べ替え

著者のホームページ：

ジョシュア・J・アルラナンダム
クリスチャン・S・カルド
マイケル・J・ディニン