Geekly Articles each Day

最小のカウント：BFS

前回の投稿で 、グラフを詳しく調べることについて話しました。 今日は、それほど重要ではないグラフ理論アルゴリズム-幅優先トラバーサルについてお話したいと思います。
前回、私たちはすでに迷路を通る方法を探すことを学びました。 私は猫の下で最短経路を見つけたいと思うすべての人に尋ねます。

問題の声明

グラフのある頂点から別の頂点へのパスを見つける必要があり、パスはエッジの数が最小でなければなりません。

アルゴリズムの説明

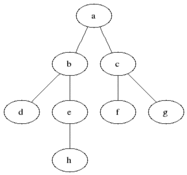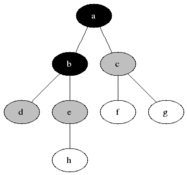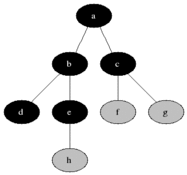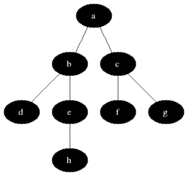
図に示すように、直観的にグラフの頂点を元の頂点からの距離の増加順に検討したいと思います。
すべての頂点を3つのセットに分割します。

明らかに、すべての頂点が黒になるとすぐに、アルゴリズムが完了します。 すべての灰色の頂点をキューに保存し、次のプロパティを維持します。すべての灰色の頂点までの距離は、キュー内にある順に単調に減少しません。
キューから最初の頂点を取得します（vで示します）。 隣接wのそれぞれについて、次の2つのオプションのいずれかが可能です。
  1. wは黒または灰色の上部です。 この場合、新しい情報は受信しません。
  2. wは白いピークです。 それまでの距離はd（w）= d（v）+ 1です。そして、距離がわかっているので、wは灰色のピークになります。

少なくとも1つの灰色の頂点ができるまで繰り返します。

実装

グラフは、ベクトル<vector <int >> edges配列に格納され、edges [v]にはvからのエッジがあるすべての頂点の数が格納されていると想定されています。 また、開始変数には初期頂点の番号が格納されていると想定されています。
Bfs
void BFS() { queue<int> q; // :      q.push(start); d[start] = 0; mark[start] = 1; //   -     while (!q.empty()) { //     int v = q.front(); q.pop(); //      for (int i = 0; i < (int)edges[v].size(); ++i) { //    if (mark[edges[v][i]] == 0) { //    d[edges[v][i]] = d[v] + 1; //     mark[edges[v][i]] = 1; q.push(edges[v][i]); } } } }


なぜ機能するのですか？

最初の頂点から到達可能な頂点vを考えます。 p [0] = start、p [1]、...、p [k] = vを、初期頂点から頂点vへの最短経路とします。 次に、アルゴリズム操作の結果として得られた値d [v] = k。
証明：
  1. d [v]≤k
    • ベース：頂点p [0] = startはアルゴリズムによって訪問され、d [p [0]] = 0
    • 仮定：頂点p [i-1]がアルゴリズムによって訪問され、d [p [i]]≤i
    • ステップ：頂点p [i-1]（またはそれ以前）を検討するとき、頂点p [i]につながるエッジを検討します。 したがって、d [p [i]]≤i
  2. d [v]≥k
    d [v] <kと仮定します。 頂点vを考えます。 頂点、考慮されるとき、頂点vは灰色に塗られました（wで示します）。 頂点、調べたとき、頂点wは灰色に塗られていました; ...; 頂点開始を開始します。 このシーケンスの2つの隣接する頂点はすべて、アルゴリズムの構築に従ってエッジで接続されます。 したがって、頂点の開始点から頂点vまでのパスがkより短い長さであることがわかりました-矛盾、したがってd [v]≥k

アルゴリズムの複雑さ

各エッジと各頂点に対して、アルゴリズムは一定数のアクションを実行するため、時間の複雑さはO（V + E）です。
キューに同時に格納される頂点の最大数はVです。つまり、使用されるメモリの最大量はO（V）です。

結論の代わりに

この記事では、最も有名なグラフ理論アルゴリズムの1つであるBFSを使用して、迷路を通る最短経路を見つけました。
次回は、私たちのお気に入りの迷路に基づいて、より複雑な問題を検討し、その例を使用して、ダイクストラのアルゴリズムを説明します。

Source: https://habr.com/ru/post/J200252/

More articles:


All Articles