🍈 🥈 🥛 指の上のハノイの塔 🌙 👲 🤷🏽

馴染みのあるプログラマーと話をしたところ、ハノイの塔について誰もが知っているわけではないことを突然発見しました。
ウィキペディアは、件名と事件について非常に厳密に書いており、何も説明していません。のように、それを真実だと考えてください。したがって、それがどのように解決されるかを理解することはすぐに困難です。しかし、タスクは非常にシンプルでありながら、プログラミングや数学的に興味深いものです。

記事には多くの写真があります。問題を再帰的に解決する方法と、バイナリ検索によって解決される方法の説明。
一般的に、この記事はハノイの塔をまだ恐れているが、恐れることをやめたい勇敢な人々に捧げられています。

ゲームのルール

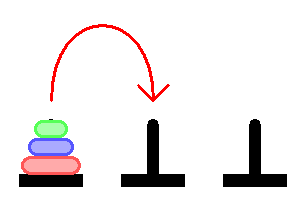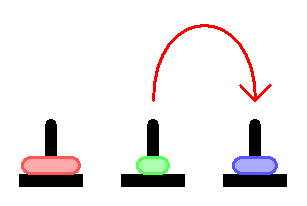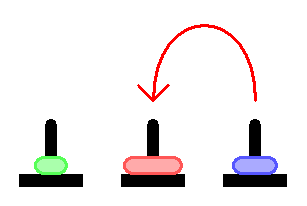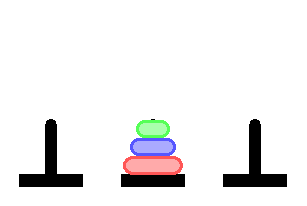
それらは非常に単純です。異なるサイズのディスクを持つ1つのピラミッドと、さらに2つの空のピラミッドがあります。ディスクをあるピラミッドから別のピラミッドに移動する必要があります。 1ターンにつき1つのドライブのみを転送できます。折り畳みディスクは小さくすることも大きくすることもできます。
したがって、このようなピラミッドがあります。

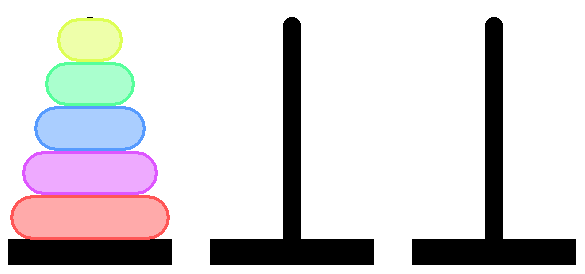
そして、我々はそれを中央の軸で言うためにシフトする必要があります。
最初からではなく、最後から問題の解決を開始した場合-それは非常に簡単であることが判明しました。考え直してみましょう。ピラミッドを2番目の軸にシフトするには、一番下のディスクをシフトする必要があります。これは、上側の4つのディスクが3番目の軸にある場合にのみ実行できます。

4つのディスクを3番目の軸にシフトするには、基本的に同じ問題を解決する必要がありますが、4つのディスクが必要です。つまり、3番目の軸で4番目のディスクをシフトできるのは、2番目の軸に3つのディスクがある場合のみです。

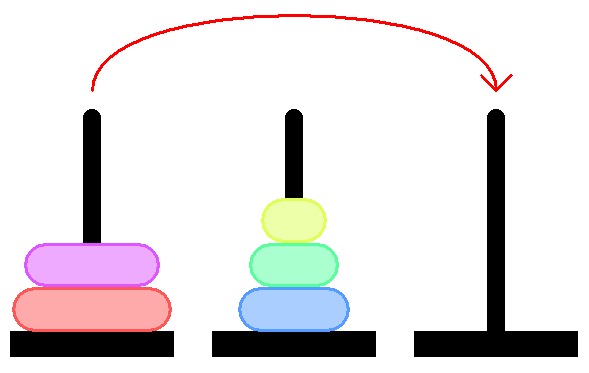
再帰を感じますか？
5台のディスクのスタックをシフトするには：
1. 4つのディスクのスタックを独立した軸に転送する
2. 5番目のディスクを必要な軸に移動します
3. 4つのディスクのスタックを必要な軸に移動する

同様に、4つのディスクのスタックをシフトすることは次のとおりです。
1. 3つのディスクのスタックを独立した軸に転送する
2. 4番目のディスクを必要な軸に移動します
3. 3つのディスクのスタックを必要な軸に移動します

以上です。

再帰的な実装

このような詳細な説明の後、これをアルゴリズム的に実装することは難しくありません。

Delphiの実装

そこで、タレットのタイプを含むモジュールについて説明しました。

unit untHTypes; interface const MaxRingCount = 5; type TTower = record RingCount: Integer; Rings: array [0..MaxRingCount-1] of Integer; procedure MoveRing(var AtTower: TTower); end; TTowers = array [0..2] of TTower; procedure InitTowers(var towers: TTowers); implementation procedure InitTowers(var towers: TTowers); var i: Integer; begin towers[0].RingCount := MaxRingCount; towers[1].RingCount := 0; towers[2].RingCount := 0; for i := 0 to MaxRingCount - 1 do begin towers[0].Rings[i] := MaxRingCount - i; towers[1].Rings[i] := 0; towers[2].Rings[i] := 0; end; end; { TTower } procedure TTower.MoveRing(var AtTower: TTower); begin Assert(RingCount > 0); Assert(AtTower.RingCount - 1 < MaxRingCount); if AtTower.RingCount > 0 then Assert(Rings[RingCount - 1] < AtTower.Rings[AtTower.RingCount - 1]); Dec(RingCount); AtTower.Rings[AtTower.RingCount] := Rings[RingCount]; Rings[RingCount] := 0; Inc(AtTower.RingCount); end; end.

TTowerは、タワーを記述する構造です。その中で、RingCountは、タワーで実際に着飾った指輪の数を保存します。リングのサイズは、Rings配列に1からMaxRingCountまで格納されます。タワーが3つあるため、TTowers型のTTowers = array [0..2]が宣言されました。
また、MoveRing機能を使用して、タワーから上部のリングを別のリングに移動できます。この関数は、Assert-sを介して操作の正確性をチェックします。
タワーソリューション自体はプロジェクトファイルにあります。

 program Hanoy; {$APPTYPE CONSOLE} uses SysUtils, untHTypes in 'untHTypes.pas'; {$R *.res} procedure SolveHanoy; var towers: TTowers; function GetThirdIndex(index1, index2: Integer): Integer; //        begin //      Assert(index1 <> index2); case index1 of 0: if index2 = 1 then Result := 2 else Result := 1; 1: if index2 = 2 then Result := 0 else Result := 2; 2: if index2 = 0 then Result := 1 else Result := 0; else Assert(False,'wrong indeces'); end; end; procedure MoveStack(stacksize: Integer; fromindex, atindex: Integer); //         var thirdindex: Integer; begin if stacksize = 0 then Exit; thirdindex := GetThirdIndex(fromindex, atindex); //   MoveStack(stacksize - 1, fromindex, thirdindex); //  ( 1 )    towers[fromindex].MoveRing(towers[atindex]); //       WriteLn(fromindex,'-',atindex); //      MoveStack(stacksize - 1, thirdindex, atindex); //        end; begin InitTowers(towers); MoveStack(MaxRingCount, 0, 1); end; begin SolveHanoy; end.

アルゴリズムの複雑さ

ピラミッドを移動するために必要なアクションの数を簡単に計算できます。
1つのディスクからスタックを移動する場合、1つのアクションが必要です。
2つのスタックがある場合、1 * 2（1つのディスクからスタックを2回移動）+ 1（最後のディスクを移動）
3つのうちの場合（（1 * 2）+ 1）* 2 + 1
5つのうち：（（（（（（1 * 2）+ 1）* 2 + 1）* 2 + 1）* 2 + 1）
したがって、各操作は2倍+ 1移動分増加します。 n個の操作の括弧を開く-取得します：
$画像$
次の値に等しいため、金額を取り除くことができます。
$画像$
ps私は頭の量を取り除いて、無限に減少する等比数列のメンバーの合計を覚えていますが、数学者がこれらの変換を正しく書く方法を示すことを望みます
全体として、すべての変換後、次のことが判明しました。
$画像$

つまり、たとえば、ハノイの塔のソリューションを64枚のディスクに記録するなど、奇妙な何かが必要な場合、十分な最新のストレージメディアがありません。実際、どこにも何も書く必要はありません。ハノイの塔の解決策はフラクタルであるため、0から+無限までのすべての数値を書き留めることと同じで、後で使用できます。

フラクタル性

はい、はい。ハノイの塔の解決策は本質的にフラクタルです。見てみましょう。各アクションが文字列に書き込まれているとします。次に、6枚のディスクの塔の場合、次のように記述できます。

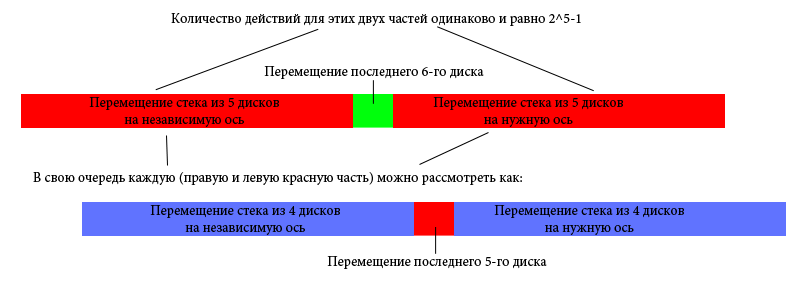
さて、これはフラクタルなので、シリアル番号のみを知っている操作には簡単に名前を付けることができます。さらに、操作時にすべてのディスクの位置を正確に復元できます。

バイナリアルゴリズム

そのため、操作の正確な数がわかり、状態を復元する操作のインデックスもわかります。
6つのディスクの塔（通常どおり、第1軸から中央軸に移動する）があるとします（つまり、2 ^ 6-1 = 63の操作があります）。49番目の操作の状態を復元する必要があるとします。
整数63を2で除算すると、31になります。これは、6番目のディスクが移動される操作のインデックスです。

49番目の操作インデックスがあります。これは、6番目のディスクがすでに中間軸上にあることを意味します。さらに、右側にあるため、5番目のディスクは3番目の軸または2番目の軸にあります。同じアルゴリズムを使用してタワーを操作するために、49番目の操作から32を引き、サブ操作インデックスを見つけます。これは17です。5つのディスクのスタックを移動するには、31の操作が必要です。5番目のディスクは16番目の操作に移動し、3番目の軸から2番目に移動します。
したがって、番号17は右にあります。

これは、ドライブ5がすでに2番目の軸に移動していることを意味します。
同様に、残りのディスクの位置を復元します。

実装（バイナリー方式）

タレットの美しいレンダリングを追加しました。同意して、コンソールログを見るのは退屈です。そのため、実装が大きくなり、記事の最後にプロジェクト全体（ソース+バイナリ）を添付します。ここであげます

Delphiの再帰関数コード

 procedure TfrmView.RestoreDisk(size, actionIndex, actionCount, fromAxe, atAxe: Integer); var pivot: Integer; i: Integer; thirdAxe: Integer; begin pivot := actionCount div 2; thirdAxe := GetThirdIndex(fromAxe, atAxe); if actionIndex = pivot then //  ,       begin //       .   FTowers[fromAxe].PutRing(size); for i := size - 1 downto 1 do FTowers[thirdAxe].PutRing(i); FAction.FromIndex := fromAxe; FAction.AtIndex := atAxe; end else if actionIndex < pivot then begin //        FTowers[fromAxe].PutRing(size); //      RestoreDisk(size - 1, actionIndex, actionCount - pivot - 1, fromAxe, thirdAxe); end else begin //          FTowers[atAxe].PutRing(size); //     RestoreDisk(size - 1, actionIndex - pivot - 1, actionCount - pivot - 1, thirdAxe, atAxe); end; end; procedure TfrmView.RestoreTowers; var index: Integer; begin ClearTowers(FTowers); index := tbOperation.Position; RestoreDisk(MaxRingCount, index, 2 shl (MaxRingCount - 1) - 1, 0, 1); Invalidate; end;

シェルピンスキートライアングル

興味深い機能を渡す際に言及したいと思います。リングの考えられるすべての動きがグラフで収集される場合、各ノードにはほとんどの場合3つの接続があります。すべてのノードと接続は、三角形の形にうまく配置できます。シェルピンスキートライアングル：

詳細については、Wikipediaをご覧ください。ソリューションのフラクタル性をすでに知っているため、一般的には驚くことではありません;）

合計

私は、一見完全に明白ではないように思えるタスクがどのように解決できるかを示すことを試みました。さらに、慎重に研究することで、問題を解決するためのまったく異なる興味深いアルゴリズムを突然発見することができ、新しい可能性が開かれます。さまざまなアプローチを探し、実験し、分析します。結局のところ、私たちはプログラマーです。
読んでくれて、記事を気に入ってくれた人に感謝します。トラックバーを使用してタレットがどのように移動するかを確認できるデモ例を添付します。

バイナリアルゴリズムの例（exe +ソースコード、Delphi）

指の上のハノイの塔