この記事では、次の質問とタスクを例として使用して、アルゴリズムをコンパイルする数学的なアプローチを示します。
- グレーのバイナリコード。 彼らの存在。 最小の変更の順序での特定のセットのサブセットの列挙。
- 最小限の変更の順序でのk要素のサブセットの列挙の存在と実装。
それでは始めましょう。
グレーバイナリコード
次数
nの グレーバイナリコードは 、すべてのシーケンスです
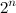nビットコード。2つの隣接するコードは1ビットだけ正確に異なります。
次数2のグレイコードの例：
そのようなシーケンスが唯一ではないことに気付くのは簡単です（少なくとも逆にすることができます）。 したがって、他の次数のグレイバイナリコードの存在を確認し、同時に、さらに処理するためにそのようなシーケンスの1種類を選択してみましょう。
存在
グレイコードの存在は、帰納法によって簡単に証明されます。
ベース-
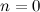
-空のシーケンス。
移行。 させて
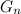
-順序のグレーコードのシーケンス
。
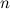
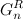
-シーケンス
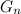
逆順で記録されます。 その後、シーケンス
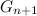
シーケンス内の各コードの左側にゼロを割り当てて取得
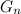
各コードの左側の単位
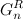
およびその後の組み合わせ、つまり
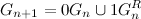
。 シーケンス内のグレイコードのプロパティを確認するのは簡単です
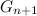
この方法で構築された違反はありません。
この方法で取得されたグレーコードは、
反射または
対称反射と呼ば
れます。 将来的には、グレーの反射バイナリコードを検討します。
演習として、証明で与えられた式を使用して、対称に反射された次数3のグレーコードを書き出します。
。
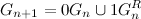
それでは、グレイコードの適用に移り、組み合わせ論のいくつかの問題を解決しましょう。
最小の変更の順序での特定のセットのサブセットの列挙
次の問題を考慮してください。「
n個の要素のセットを指定します。 すべてのサブセットを、1つの要素を
削除または
追加することで （つまり、変更が最小限の順序で）前のサブセットから取得されるように表示する必要があります。
セットの要素には
1から
nまでの番号が付けられていると仮定します。 次に、セットの要素の任意のセットを
nビットのバイナリコードに関連付けることができます。セットの
i番目の要素がセットに含まれている場合、コードの
i番目のビットは1、それ以外の場合はゼロです。 したがって、すべてのサブセットの列挙は次数
nのバイナリコードの列挙に削減され、最小変化の順序でのサブセットの列挙はバイナリグレイコードの列挙になります。
グレイコードの再帰列挙アルゴリズムのアイデアは、それらの存在の証明、すなわち、その中で与えられる再帰関係から確かに続きます。
。
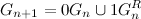
実際、証明で述べられているように、次数
nのグレイコードは、左にゼロを割り当てること
により 、次数
n-1のグレイコードから取得されます（これは関数呼び出しに対応します
およびその前の割り当て）と、左にユニットを割り当てること
による次数
n-1のグレイの逆コード（これは関数呼び出しに対応します）
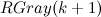
そして彼の前での割り当て）。
このアルゴリズムの複雑さを評価します。 明らかに、関数呼び出しツリー
は、高さ
nの完全な二分木です。 したがって、次数
nのグレイコードを生成するときの関数呼び出しの総数は、
、これは可能なすべての
nビットコードの数に等しい。 したがって、アルゴリズムは最適です。
演習として、読者は以下の短い再帰検索アルゴリズムを分析するように求められます。
また、反復検索アルゴリズムの存在と、この記事では考慮されておらず、ウィキペディアなどの他のソースから学習できるグレイコードのその他の有用なプロパティについても述べたいと思います。
それでは、最後の最も興味深いタスクに移りましょう。
最小の変更の順序でのk要素のサブセットの列挙。
問題のステートメントから始めましょう。「
n個の要素のセットが与えられます。 正確に
k個の要素から構成されるすべてのサブセットを導出する必要があります。これにより、後続の各サブセットは
、正確に1つの要素を
置き換えることによって（つまり、最小の変更の順序で）前のサブセットから取得されます。
ここで、前の問題からのアルゴリズムのアイデアがすぐに思い浮かびますが、正確に
k単位のグレーコードのみを印刷します。 これは、このアルゴリズムの正確性の問題を提起します：誰もが隣接するコードが順番に並んでいることを保証しません
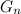
、ユニット数が
kに等しいバイナリコードのみが残り、1つの要素を置き換えることで相互に取得された最小の変更の順序で、正確に2桁の差で配置されます。 したがって、対称反射グレーコードの特性のさらなる研究に進みます。
いくつかの表記法を紹介します。
文字xを連結（ m回）し、文字yを連結（ k回）した文字列です。 例：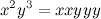 
。
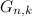k単位のすべてのnビットコードのシーケンスです。コードは、シーケンス内に配置されている順序になります。 。
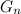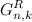k単位のすべてのnビットコードのシーケンスです。コードは、シーケンス内に配置されている順序になります。 。
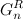補題
最初のバイナリコード
順番にユニット
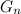
形をしています
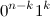
そして最後の
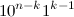
または
もし
。
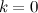
証明
上の帰納法で証明する
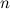
そして
。
ベース-
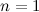
-true（2つのコード0および1の上記の式を簡単に確認できます）。
移行。 式を真とします
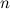
および
。 グレイコードの存在の証明から式を思い出してください。
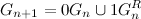
。 ここから、最初のコードを取得します
順番にユニット
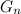
左側にゼロが割り当てられているのは、
順番にユニット
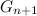
。 で
唯一のコードを取得します
式も真である単位。 で
最後のコード
順番にユニット
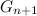
で最初のコードを持っています
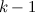
ユニットおよびシーケンスの左に割り当てられたユニット
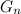
。 で
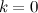
式も真です。
定理
連続したバイナリコード
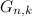
2つのカテゴリがまったく異なります。
証明
また、帰納法で証明します
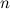
そして
。
ベース-
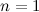
-明らかに（シーケンス内の1つの可能なコードのみ）。
移行。 定理を保持しましょう
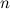
そして
。 で
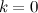
または
シーケンスにはコードが1つしかありません
。 で
隣の言葉は完全に
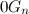
または
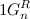
帰納法の仮説により、それらは2桁で正確に異なります。 隣接するコードのペアを検証するには
最後のコード
単位
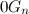
と最初のコード
単位
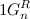
（最後に
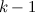
ユニットイン
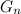
ユニットが左に割り当てられています）。 補題により、
彼らは形をしています
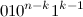
そして
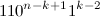
それぞれ、いつ
-
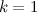
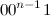
そして
。 正確に2つのカテゴリが異なることは簡単にわかります。
これで、定理の顕著な結果を述べることができます。
- 前に提案した単純なアルゴリズムは正しいです。つまり、シーケンス内にある場合 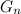正確にk個のユニットが存在するバイナリコードのみを残し、それらは最小の変更の順序で配置されます（各要素は、前の要素から1つの要素を置き換えることで取得されます）
- シーケンス 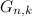次の繰り返し関係によって定義されます：
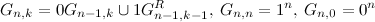。 これは、誘導によって検証できます。 - シーケンス 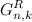次の繰り返し関係によって定義されます：
。 また、誘導によって検証されます。
これらの結果を使用して、
k要素のサブセットを最小限の変更の順序で再帰的に列挙するプログラムを作成できます。
バイナリコード出力は、
uと
vの値に応じて、残りのビットを1または0で埋めることを意味するという事実に注意を喚起したいと思います。
提示されたアルゴリズムの複雑さを推定します。 再帰を深くすると、
uの値は常に減少することに注意してください。 つまり、バイナリコードを実現するために、
n個以下の凹部を作成します。 合計でそのようなコード-
。 結果の漸近線を取得します
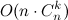
。 これはかなり大ざっぱな見積もりですが、すべての方が良いです
、特に
kが
nになる傾向がある
場合 ：アルゴリズムはほぼ線形です。
コールツリーがわかりやすい
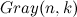
バイナリになりますが、完全ではありません。 木の観点から複雑さの評価の類似点を描いてみましょう。各葉はいくつかのバイナリコードを受信することに対応し、木の葉までの距離は
nを超えません。 格付け
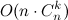
は、シートへのすべてのパスの長さ
-n-の上限を合計したことを示しています。 しかし、結局のところ、これらのパスの多くは
nより短い長さを持ち、さらに多くのパスが互いに交差しています。 これは、提示されたアルゴリズムの漸近的な振る舞いが実際にははるかに優れているという考えにつながるはずです。
漸近現象の正確な推定は、E。Reingold、J。Nivergelt、およびN. Deoの本「Combinatorial Algorithms。」に記載されている些細な事実からはほど遠いものです。 理論と実践」、またはそれを自分で証明してみてください。
これで私は記事を終了したいと思います。 ありがとう、また会いましょう。