応用数学では、次の形式の常微分方程式の正規システムの周期解を構築する問題が生じることがあります。
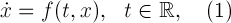
関数はどこですか
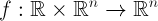
量を表します
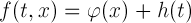
多次元多項式
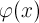
および三角多項式
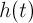
ある
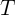
-周期ベクトル関数。
システム（1）の周期解の存在定理の多くは、そのような解がシステムの軌道に沿ったシフト演算子の不動点によって完全に決定されるという基本的な事実を使用しています。 ただし、これらの定理を使用して必要な定期的な解決策を直接見つけることはほとんど不可能です。
システム（1）には一意の
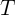
-周期解
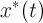
。 ユニークな周期解を持つシステムの例は、収束のあるシステムです（Pliss V. A.振動理論の非局所的問題。-M.、L。：Nauka、1964）。 そのようなシステムの1つのクラスについて、解の近似値を構築できます。
。
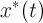
させて
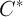
そのベクトルは
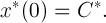
ここでは、推論を簡単にするために、最初の瞬間がゼロであると仮定します。 次に、ベクトルを決定できる場合
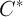
、その後、目的の定期的なソリューションを構築することができます。
関数に課せられた条件を紹介します
：
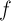
1.させる
-解の値を含む半径
rの閉じたボール
、
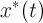
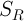
半径
Rの閉じたボールであり、
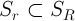
、そしてそのような正の数があります
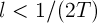
のために
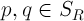
不平等がある
2.そのような正の数があります
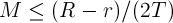
みんなのために
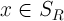
および
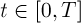
不等式が成り立つ
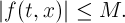
図 図1は、2次システム（1）のこれらの条件の図解を示しています。
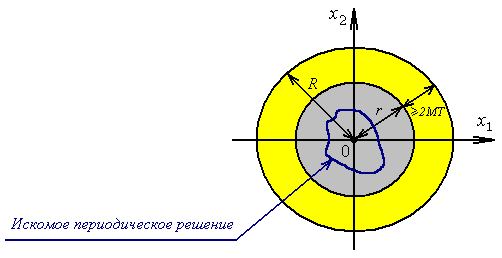図 1. 2次システムの条件1-2の図。私の仕事では、この場合、連続近似が示されています
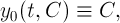
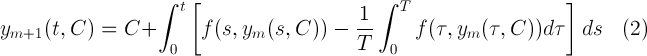
任意のベクトル
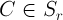
すべてに対して均一に収束する
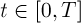
何らかの機能へ
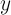
。 また、選択した場合
、それが判明した
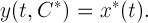
式（2）に基づいて、各反復は記号形式で計算されます。 さらに、積分の下で三角関数を変換した後、常に平均積分値がゼロの三角多項式を取得できます。 周期解の近似を表す分析形式は、この近似を構成する高調波を分析できるという点で便利です。 次の反復を計算した後、関数が構築されます
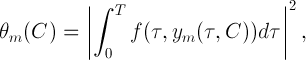
その最小値はベクトルの近似値を与える
。
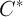
例として、形式（1）の収束を伴う2次の非線形システムが考えられました（ボールの半径の値は作業で示されます）。
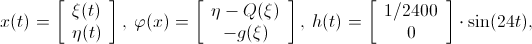
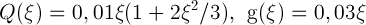
。 1回目と2回目の繰り返しで、見つかったベクトルの近似値が
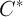
同じです
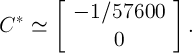
見つかった開始点に対応する調査中の2次システムの軌道は、一定期間後にその近傍に戻ることが確認されました（図2）。
図 2.見つかったベクトルに対応するパスの円弧 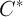。このトピック
については、数学の会議で
私のレポートを見ることができます（ビデオの品質をおaびします-電話で撮影されました）。