この記事では、Wolfram Mathematica環境を適用して、微分方程式の複雑なシステムの解法、解の結果のグラフィカルな解釈、手続き型プログラミング要素の物理的問題への適用、剛体運動の例を使用する方法を示します。 この記事の本質は、コンピューター代数ツールを使用して、19世紀の物理学者の心を刺激する複雑な物理システムを簡単かつ簡単に分析する方法を示すことです。
球体運動について少し
球面運動-1つの固定点を持つ
TTの運動。 この動きのある
TTの各ポイントは、アタッチメントポイントを中心にして球体の表面に沿って移動します。 この場合、固定点を通過する瞬間的な回転軸の周りの一連の基本的な回転で構成される回転運動について話します。 瞬間的な回転軸は、移動が考慮される基準フレームと本体自体の両方に対して連続的にその位置を変更し、それぞれ固定および可動軸と呼ばれる2つの正準面を形成します。
固定小数点
CTには3つの自由度があり、特定の参照フレームに対するその位置は、3つのパラメーター、またはオイラー角によって決定されます。 これらの角度はシステムの3回転を定義し、これによりシステムの任意の位置を電流に近づけることができます。
対応する角度
Ψ 、
θ 、および
φによってZ、X '、Z' 'の順序でZ軸およびX軸の周りの
SCの基本回転を取得すると、そのような変換はオイラー角に関する回転行列の表現につながります。 このようなマトリックスを使用して、
TTは空間で回転します。
使用される角度には、次の物理的意味があります。
- 角度Ψ-歳差角
- 角度θ-章動角
- 角度φ-適切な回転角度
Leonard Euler（ドイツ語：Leonhard Euler）によって最初に記述された
TTの球面運動は、次の3つの場合にのみ解決策があります。
- オイラーの場合-TTの重心は固定点にあります。 外力のモーメントはゼロです。
- ラグランジュの場合-TTは動的に対称です
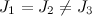。 CTの重心は対称軸上にあります。 - コバレフスカヤの場合-身体は動的に対称的であり、慣性モーメントは関係によって関連しています
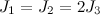。 TTの重心は赤道面にあります。
次に、ラグランジュの場合の重い対称トップの動きについて説明します。
ラグランジュの場合の運動方程式
重力場で重い対称トップの図面を描きましょう。 上部の役割はコーンに割り当てられます。
運動方程式を運動モーメント定理から取得します。これは、以前に可動
SCで一般形式で記述されていました。
ここで、作成した図面と書き留めた定理を使用します：面倒な公式を省略し、対称頂点の慣性モーメントを考慮して、同様のものを提示し、重力場における
TTの運動方程式系を取得します。
このシステムは厳密に分析的に解かれているわけではなく、解は求積法でのみ提示されています。 このシステムを数値的に解決し、結果を分析します。
Wolfram Mathematicaシステムでのラグランジュのケースのモデリング
まず、
リモートコントロールシステムの初期条件を設定する必要があります。
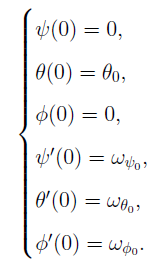
さらに、コンピューター代数システムの機能を使用して、頂点のパラメーターを設定し、プリミティブを描画し、
制御システムを数値的に解きます。
次に、組み込みの言語ツールを使用して、先ほど説明した回転行列を取得し、そこで数値解法を置き換え、この「ケーキ」に幾何変換演算子を適用します。
それは基本的に数行のソリューションのすべての複雑さです。 グラフィック領域を決定し、モーションの軌跡を作成し、アニメーションを作成することだけが残っていますが、これはすでにアマチュアに言われているとおりです（変換行列の数値的導出に制限することができます）。 コードの残り：
Wolfram Mathematicaシステムでの結果の結論と分析
プログラム結果の出力は、モーションの初期条件、アニメーション時間、上部の透明度の動的パラメータを備えたウィンドウの形式で実行されます。
重力場での
規則的な（強制的な）歳差運動の場合の頂点の挙動を分析しましょう：
運動モーメント定理（上記で説明しました）によると、時間
dtごと
に 、角運動量ベクトルは重力の作用下で増分を受け取ります
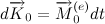
に沿って指示
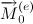
、つまり 上部の軸に垂直な水平面に横たわっています。 その結果、角運動量のベクトルとそれに伴う上部の軸は、支点を通る垂直線を中心に均一に回転します（歳差運動）。 上部が垂直歳差に曲がっています。 独自の軸を中心に回転することに加えて、垂直軸を中心に回転します。 高速で適切な回転を行うと、この歳差運動（垂直軸周りの回転）が非常にゆっくりと発生するため、垂直周りの歳差運動によって生じる角運動量の成分を精度よく無視できます。 上部軸のこの動作は、通常の歳差運動と呼ばれます。 これは重力モーメントの影響下で発生するため、強制歳差運動です。 その軸上にある頂点のすべてのポイントは、円形のパスに沿って均一に移動し、その中心は頂点の支点を通る垂直線上にあります。 図は、上部の通常の歳差運動を示しています。
このイベントは、厳密に定義された初期条件でのみ発生します。
これで、通常の歳差運動が即座に発生しない初期条件下で、重力の作用下でコマがどのように振る舞うかという問題の研究に進むことができます。 一般的なケースでは、図に示すように、上部の動きは、強制的な通常の歳差運動と章動の重ね合わせになるはずです。
最初の瞬間、重力の影響下でトップの軸を離すとすぐに、実際に落下し始めます。これは、直感的なアイデアと非常に一致しています。 しかし、軸が速度を上げると、その上端の軌道は垂直からますます逸脱します。 すぐに、通常の歳差運動と同様に軸の動きは水平になりますが、この運動の速度は通常の歳差運動に必要な速度よりも大きくなります。 軸の端の軌跡が上方向にずれ始めます。 元の高さまで上昇すると、軸は「フリーズ」し、速度が消滅します。 その後、すべてが最初に繰り返されます。 しかし、軸の端がサイクロイド軌道に沿って移動するとき、どのような動作を理解するかは、2つの動きの追加によって説明されます-角の運動量ベクトルの周りのトップの章動と、垂直の周りのこのベクトルの同時強制歳差運動。
章動が小さい場合、強制歳差運動は擬似正規と呼ばれ、図ではこの現象を観察できます。 テクノロジーで使用される高速回転ジャイロスコープ（つまり、非常に高速な回転ジャイロスコープ）の場合、擬似正規歳差運動は実際には通常の歳差運動と変わりません。 そのような場合、章動は、ジャイロスコープの軸のかろうじて目立つ小さくて頻繁な震えとして現れます。 さらに、小規模章動は摩擦力の作用により急速に減衰し、擬似規則的歳差運動は規則的になります。
おわりに
したがって、Wolfram Mathematicaなどの強力なツールを使用すると、プログラミングに関する多くの労力と知識がなくても、そして最も重要なことには、古典的な教科書が示唆するように、興味深い神秘的なプロセスと現象を観察できます。 主なことは、システムのパラメーターを個別にツイストおよび回転できることです。これは、理解にとって非常に重要です。 このプロジェクトは私の任期論文であり、私は数か月間そのプロジェクトに取り組みましたが、結果には満足していました。 長い間、トップのモーションのアニメーションをひねり、LagrangeやKovalevskayaにはなかったさまざまなモーション軌道を観察するパラメーターで遊んでいました。
文学
- Wittenburg、J. Dynamics of solids / J.Wittenburg。-モスクワ：MIR、1980.-294 p .:
- 回転運動。
- オイラー角。
- ジャイロスコープの強制歳差運動。
更新しました。 労働者のリクエストにより、DropBoxにプロジェクトをアップロードしました
Wolfram Mathematica 9.0で使用される
- CDFプロジェクト。
- nbプロジェクト。